数学复习课构建知识体系的教学探析

摘要：数学复习课既要引导学生对本章所学知识内容进行梳理回顾，更要帮助学生对所学知识之间逻辑关系的体系进行整体建构。以中职“指数函数与对数函数”教学为例，阐明在复习课教学过程中关注知识之间的共性、特性以及内在逻辑关系的重要性和必要性，结合案例探讨复习课重视知识体系建构对关注学习要点、明确学习重点、化解学习难点、培育学科核心素养、提升学习能力等方面的意义。

关键词：复习课;知识体系建构;课例研究

中图分类号：G712 文献标志码：A 文章编号：1673-9094-（2019）10C-0015-05

复习课是一种重要的课型。数学复习课一方面通过回顾知识内容进一步明确学习重点、化解学习难点，另一方面通过建构知识体系厘清概念之间的关联和知识点之间的关系，是培养学生数学学科核心素养的重要载体。本文以“幂函数、指数函数与对数函数”（以下称“三种基本初等函数”）章节内容的复习为例，阐述在复习课进行知识体系建构的教学策略与价值。

一、明确学习重点，厘清概念关系

复习课在新授课之后，学生已经学完了本章节的基础知识，但大部分学生仍停留于“学了什么知识”“怎样学”，对于“如何用”以及举一反三的能力未较好地形成。因此，章节复习课需要通过复习、比较、建构等环节，帮助学生弄清过去已知、现在所学以及未来要学的知识之间的关联，为以后“怎么学，怎么用”奠定知识、能力和素养基础。

（一）同化新知，拓展幂指数认知范围

中职学生对幂概念的深入学习是基于初中已有知识基础之上的拓展学习，是进一步学习幂函数、指数函数、对数函数的基石。 “幂函数、指数函数与对数函数”章节复习课上，学生已经知道了三种基本初等函数的相关概念、图象以及性质，并初步掌握了直接运用所学知识解决部分问题的方法。复习还需要挖掘旧知识与新知识之间的关联，比较知识之间的异同，运用所学特别是知识交汇来解决实际问题。

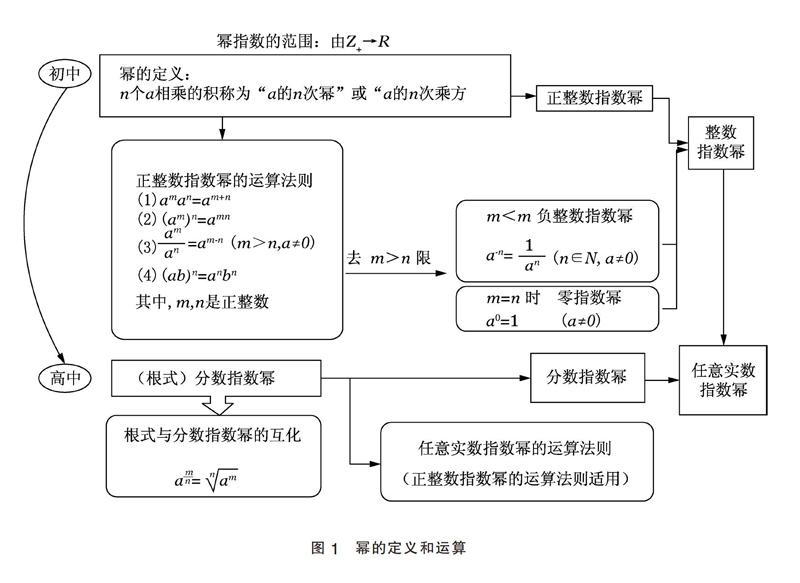
教学遵循学生认知发展规律，以学生已经习得的知识为线索展开，通过比較厘清新旧概念之间的关系，对知识体系进行建构。例如，与初中相比，中职本部分知识内容除了“将幂指数的范围由正整数推广到了实数”外，只增加了“分数指数幂与根式互化”部分内容。在幂指数范围的扩充、实数指数幂的运算法则内容的复习中，引导学生认识到：与初中“幂的运算”内容学习相比，无论是知识体系还是知识内容都是一致的，中职所学仅有指数范围不同，实质上是由整数范围扩充到了一切实数范围，这样新问题就转化成了旧问题，变得简单了。

（二）巩固新知，辨析相关函数概念

幂函数、指数函数、对数函数概念对学生来说是初中所学函数内容的拓展，从概念角度辨析它们之间的关联是帮助学生准确区分它们的关键。准确界定相关概念需要搞清以下四个方面的问题。

第一个问题是基本初等函数的分类是什么？高等数学将基本初等函数归为五类：幂函数、指数函数、对数函数、三角函数、反三角函数;数学分析将基本初等函数归为六类：幂函数、指数函数、对数函数、三角函数、反三角函数、常数函数。以上函数在中职均有涉及，其中容易被混淆的是幂函数、指数函数和对数函数。

第二个问题是三种基本初等函数的共性是什么？与初中学过的一次函数、反比例函数、二次函数定义的方式相同，幂函数、指数函数、对数函数也是形式定义：形如y=xα（α为有理数）的函数叫幂函数;形如y=ax（a>0，且a≠1） 的函数叫指数函数;形如y=logax（a>0，且a≠1）的函数叫对数函数。

第三个问题是如何区分三种基本初等函数？回答这个问题需要探寻并抓住相关数学概念中的本质特征。幂 ab=N中，未知数在哪个位置就是什么函数。如y=ax未知数x在指数位置，所以是指数函数;y=xa未知数x在幂（底数）位置，为幂函数。同一个a的指数函数和幂函数是成反函数关系，是关于直线y=x对称。

最后一个问题是三种基本初等函数之间的关联是什么？应当引导学生深入分析、比较、归纳，抓住函数概念的核心要素。进一步明晰三种基本初等函数之间客观存在着的两两关联关系。如，指数函数y=ax与对数函数y=logax互为反函数。

二、化解学习难点，建构知识体系

“指数函数与对数函数”是基础模块部分的学习内容。《中等职业学校数学课程标准》（征求意见稿）规定的学习内容和要求包括：了解有理数指数幂和实数指数幂的相关概念、理解实数指数幂的运算法则;了解指数函数的定义、理解指数函数的图像和性质;了解对数的相关概念及性质、了解对数的运算法则、了解对数函数的图象和性质;初步掌握从实际情境中抽象出指数函数、对数函数模型解决简单问题的方法。在实际教学中，这部分内容是学生进入中职阶段再识“函数概念”后研究的具体函数，与以前的学习基础与学习经验并不完全相同，这也成为部分学生的学习障碍。教师解决这个问题可以尝试通过关注学习基础和知识要点，帮助学生通过建构知识体系等方式来化解。

（一）关注学习基础，尝试比较学习

中职学生在初中阶段数学学习基础与能力普遍欠佳。数学中有不少概念是借助于抽象建立并发展的，概念的获得要求学生掌握一类事物的共同本质属性，并能辨别本质属性和非本质属性，能列举出概念的例证和反例。然而，数学抽象思维要求给不少中职学生带来学习困扰，有些学生甚至排斥学习数学。

比较学习是一种常用而有效的学习方式。以对比双方的相似、相近或相对的属性为切入点探究所学概念，进而对知识的本质属性进行理解。数学教学中常常通过比较知识之间的关联，并按特点对它们进行归类，来达成厘清概念、理解原理的教学目标。例如，教师在讲解“幂函数的概念”环节时，可以设置两个问题引导学生比较并思考“我们已经学过一次函数、反比例函数、二次函数，关于函数学习，你有哪些学习经验”，引导学生从已有对函数的定义、图象的经验出发，根据函数的图象来研究函数的性质。可以让学生思考“比较一次函数、反比例函数、二次函数的定义方式，你能给幂函数下一个定义吗”，引导学生通过比较已学概念定义方式的共同点，来同化新知。

（二）关注知识要点，解决突出问题

抓住函数概念的本质特征辨析函数概念。复习时需要引导学生进一步比较初中、中职关于函数概念表述的相同和不同之处，能够接受并逐步习惯从映射的角度来理解函数的概念;掌握指数函数与对数函数的图象知晓函数性质，能熟练画出指数函数在底数a分属01两种不同情况下的简图并能根据函数图象说出函数的相关性质;知道说函数性质应该从哪几个方面进行表述;明晰指数式与对数式之间的关联并能熟练将给定的对数式与指数式进行互化;能依据函数的定义，准确写出它们的定义域和值域。关于对数的运算性质、对数恒等式、运算法则等公式要在结合幂的运算相关规律的基础上来理解，进一步理解对数式与指数式之间的关系。例如，从运算法则的形式上来看，任意实数指数幂的运算法则与初中学过的正整数指数幂的运算法则完全一致;从本质上来看，是将幂指数的范围由整数推广到一切实数之后的旧知拓展学习。

（三）建构知识体系，化解学习难点

通过比较建立起来的知识可以有效帮助学生化解学习过程中遇到的“概念不清”等学习问题。

1.实数指数幂部分：引导学生以比较的形式建构基于已有学习经验基础上的实数指数幂知识体系。

实数指数幂部分的知识要求包括：识记n次方根以及根式的概念及性质，辨别奇次方根、偶次方根、n次算术根之间的区别，理解分数指数幂、有理数指数幂的定义及运算，掌握实数指数幂的综合运算等。这些内容看起来零散，导致学生不易掌握。教师可以通过建构初中、高中关于幂的相关概念、运算的异同，比较知识体系，帮助学生从已掌握的知识内容和学习经验入手，比较新知与旧知之间的区别与联系，从而引导学生掌握新概念、新规律。

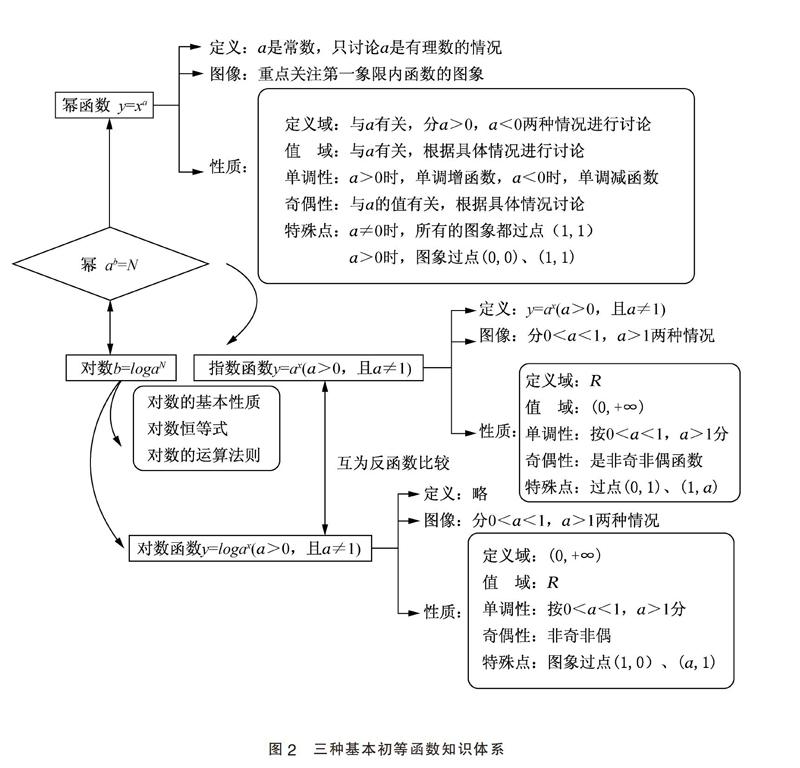
2.复习小结部分：引导学生以比较的形式建构三个基本初等函数之间知识关系体系。

从三个基本初等函数本身来看，它们之间客观存在着不可割裂的内在联系，从学习要求、学习方法等方面来看，也存在着很多的共性。学习完三个基本初等函数后对知识内容和内在逻辑关系进行比较、梳理十分重要和必要，我们通过建构知识体系来比较它们的定义、图象和性质特点，从而进一步厘清它们之间的区别与联系，达成教学目标要求。

三、再识能力方法，发展核心素养

《中等职业学校数学课程标准》（征求意见稿）中指出：中等职业学校数学课程是中等职业学校学生必修的一门公共基础课程，承载着落实立德树人的根本任务、发展素质教育的功能。中等职业教育数学学科核心素养是具有中职学校数学课程的基本特征的思维品质、关键能力、情感态度与价值观的综合体现。在数学章节复习课型建构知识体系可以助力学生对基础知识、学习能力以及学习方法的再识，通过解决实际应用问题体会数学的工具性、数学知识多样性以及数学学习的有趣性等特点。

（一）再识学习内容

在数学章节复习课上通过构建知识体系可以帮助学生再识新旧知识之间的关联。对教授过的内容进行再识是巩固所学的重要认知环节，也为运用所学解决问题奠定知识基础。有效组织实施的关键在于教师要充分发挥好“导”的作用，引导学生将一个个知识“点”串成知识“线”，最后形成知识“体”。

例如，教师引导学生从复习正整数指数幂相关内容切入，再识指数从整数范围到有理指数再到实数范围的推广过程、指数式与对数式的互化;再识用“描点法”画指数函数与对数函数图象、根据图象描述函数的性质，感知其变化的规律，学生可以尝试画一画知识框图或思维导图，在厘清知识要点后，尝试运用所用所学建立指數函数和对数函数的应用模型来解决简单的实际问题，运用计算器等工具熟练进行指数和对数的运算等。

（二）再识学习方法

在数学章节复习课上通过构建知识体系可以帮助学生总结提炼适合自己的有效学习方法。学习方法是学生经过反复学习实践的过程逐步培养获得的。掌握学习方法的关键在于学生具备认真学习的态度、勇于实践的精神和勤于建构知识体系的习惯。

例如，教师引导学生思考幂式 ab=N（a≠0）所涉及的三个量a、b、N，从“知二求一”的角度来看，幂、指、对这三种基本初等函数复习的先后秩序可以自主确定，反推至知识建构的次序上，学生也可以尝试从a、b、N三个量中择其一开始复习，通过比较不同函数的概念、性质、运用等知识方面的异同来建构知识体系，引导学生获得选择适合的学习方法给自己带来的成功体验。

（三）再识核心素养

在数学章节复习课上通过构建知识体系同样可以培育“数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析”等核心素养。这些能力素养都是通过数学学科教学和综合实践活动课程实施、在数学学习和应用的过程中逐步形成和发展的，在复习课上建构知识体系也是一种重要的教学活动。

例如，如图2建构知识体系的过程关注了知识点的复习和统合，再一次强化了学生初步具备“数感、符号、直观、推理”等能力;又通过运用知识解决问题来提升学生“应用意识和创新意识”，进一步培养“运算、分析、建模”等能力。这些能力点都是数学学科核心素养的关键点。

综上所述，重视章节复习课教学设计与实施，以及学生参与与实践是提升数学课堂教学实效的两个重要方面。融学科素养与职业素养的能力点于复习课知识建构过程，是让学科教学更好地助力学生掌握专业知识的重要途径。

参考文献：

[1]徐章韬.数学单元小结课的认识及其教学设计[J].课程˙教材˙教法，2016（12）.

[2]樊玉敏.《数学》第四章“指数函数与对数函数”教学建议 [J].江苏教育.2013（5）.

[3]樊玉敏. 以形助数 以数辅形[J].中学数学教学参考.2018（5）.

责任编辑：夏英

On the Teaching of Constructing Knowledge System in Mathematics Review Courses： A Case Study

FAN Yumin

（Nanjing Xuanwu Secondary Vocational School， Nanjing 210042， Jiangsu Province）

Abstract： The Mathematics review course should not only guide the students to sort out and review the contents of this chapter， but also help the students to construct the system of logical relationships among the learned knowledge as a whole. Taking the teaching of "Exponential function and logarithmic function" in secondary vocational schools as an example， this paper expounds the importance and necessity of paying attention to the commonness， characteristics and internal logical relationships among knowledge in the course of review teaching， and discusses the importance of knowledge system construction in review teaching in terms of paying attention to learning key points， clarifying learning priorities， resolving learning difficulties， cultivating core quality of disciplines and improving learning abilities.

Key words： review course; knowledge system construction; lesson study

本文系第四期江蘇省职业教育教学改革研究重点资助课题“中职数学‘四维多元数字化课程资源开发与运用的校本研究”（课题编号：ZZZ3）阶段性研究成果。

收稿日期：2019-09-10

作者简介：樊玉敏，南京市玄武中等专业学校（江苏南京，210042）副校长，高级教师，主要研究方向为中职数学教学。