二次曲面共形整流罩像差影响因素分析
张运强,常 军,潘国庆
(1.北京理工大学 光电学院,北京 100081;2.中国空空导弹研究院,河南 洛阳 471000;3.航空制导武器航空科技重点实验室,河南 洛阳 471000)
引言
红外成像制导武器具有分辨率高、作用距离远以及抗干扰能力强等优点而得到广泛应用。红外整流罩位于导弹的最前端,起到保护内部元件免受外部环境侵蚀及整流的作用。光学成像系统位于整流罩后端并围绕着回转中心转动[1-2]。红外整流罩传统上采用半球形,且稳定平台的回转中心与球心重合。采用球形整流罩的优点是稳定平台跟踪过程中整流罩引入的像差不随视场变化,但是球形整流罩的空气阻力系数大,不利于导弹飞行速度的提高。因此,为了减小空气阻力系数、提高武器的作战性能,提出了共形光学技术的概念[3-4]。共形光学技术的发展始于1996年美国国防部高级研究计划局DARPA实施的“共形光学计划”。该计划汇集了雷声公司、波音公司、辛克莱光学、罗切斯特大学以及亚利桑那大学等世界一流的科研机构[1,5],并研制出世界上第一台共形光学系统样机。共形光学技术的提出及相关研究成果为高速导弹整流罩的设计指出了新的发展方向,并持续成为研究热点之一。
共形整流罩的外表面在优化时首先考虑空气动力学性能,其次才考虑光学成像性能,具有更尖的外形[6]。与传统的球形整流罩相比,共形整流罩的对称性由点对称性退化为面对称性,不同跟踪场下整流罩参与成像的部分不同。由于共形整流罩失去点对称性,不同跟踪场下成像时会引入大量的非对称像差,且该非对称像差会随着跟踪场的变化而变化。因此,共形光学技术的核心在于校正共形整流罩引入的非对称像差,需要解决的技术难点包括设计、加工、装配以及检测技术[7-8]。目前,已提出的像差校正方案包括固定校正器、弧形校正器、可变形反射镜校正器、轴向平移位相板校正器、轴向移动柱面镜以及反向旋转位相板等。各方案在一定目标视场内均有较好的校正效果。为了扩大目标视场,一般采用两种或两种以上结合的校正方案[6,9]。本文将对共形整流罩的像差特性进行分析,研究各项因素对像差的影响规律,为共形整流罩的设计提供依据。
1 共形导引头的结构及主要参数
共形光学系统包括共形整流罩、校正器及成像系统,其结构如图1所示。其中,L为整流罩外表面顶点到底部的距离,D为整流罩的底部直径,D0为成像系统的入瞳直径,O′为成像系统的回转中心,z0为整流罩顶点到回转中心的距离。共形整流罩的长径比是影响导引头空气动力学性能的重要参数,定义为外表面顶点到底部的距离和底部口径的比值(L/D)。随着整流罩长径比的增大,导引头的空气阻力会显著减小。此外,瞬时视场和目标视场是导引头的另外两项重要参数。瞬时视场(FOV)描述了导引头在某一时刻可观测的范围,其大小主要由成像系统的焦距和探测器光敏面的大小决定,如图1所示。某一时刻,成像系统光轴与对称轴的夹角称为视角(LA)。最大的视角定义为跟踪场(FOR)。跟踪场表示成像系统围绕转动中心的最大扫描范围,其大小决定了搜索目标的范围。口径比定义为成像系统入瞳直径与整流罩底部直径的比值(D0/D),其大小反映了共形光学系统的能量利用效率[10-11]。当弹体外部直径确定时, 增大口径比可显著提高光学系统的进光量。

图1 共形光学系统结构示意图Fig.1 Structure diagram of conformal optical system
目前,主要研究的共形整流罩外表面为二次曲面,并且以椭球形居多。在设计内表面时,一般采用和外表面相同的表面类型,且具有相同的厚度和边缘斜率[7,12],如图2所示。其中,t为整流罩在顶点和底部的厚度,α为底部切线与z轴的夹角[13]。

图2 具有等厚内表面的二次曲面共形整流罩Fig.2 Quadric conformal dome with equal thickness inner surface
二次曲面外表面可表示为[13]
φ1(z)=[2R1z-(k1+1)z2]1/2
(1)
(2)
(3)
(4)
式中:R1是二次曲面的基圆半径;k1是二次曲面系数;Se是外表面的边缘斜率。对于给定的长度L和底部直径D,当边缘斜率取值为[0,D/4L),D/4L和(D/4L,D/2L)时,二次曲面分别对应椭圆、抛物面和双曲面[14],如图3所示。

图3 不同边缘斜率的二次曲面(D=120 mm, L=120 mm)Fig.3 Schematic diagram of quadric with different edge slopes(D=120 mm, L=120 mm)
同理,对于顶点和底部边缘厚度为t、边缘斜率为Se的二次曲面内表面可以表示如下:
φ2(z)=[2R2(z-t)-(k2+1)(z-t)2]1/2
(5)
(6)
(7)
2 像差影响因素分析
相比球形整流罩,共形整流罩在大幅减小空气阻力的同时引入了大量随跟踪场变化而变化的动态像差,校正像差是共形光学系统的核心任务。由于共形光学系统在非零目标视场失去旋转对称性,对动态像差的研究不能采用传统的赛德尔像差理论,通常将系统光瞳处的波面分解为Zernike多项式来研究。Zernike多项式是相互正交、线性无关的,可以唯一地描述圆形孔径波前形变。Zernike多项式中的每一项都有明确的物理意义,对应特定的像差,是研究波像差的理想工具[15-16]。前9项Zernike多项式及对应的像差如表1所示。

表1 Zernike多项式及对应的像差Table 1 Zernike polynomial and their corresponding aberrations
相关研究表明,共形整流罩引入的像差以离焦像差、像散、彗差和球差为主,分别对应Zernike多项式中的Z4(离焦)、Z5(像散)、Z8(彗差)和Z9(球差)。一般情况下,整流罩的底部直径由弹体大小决定,其他可供光学设计人员自由设计的参量包括长径比、外表面面型、成像系统的口径以及回转中心的位置。因此,本文针对二次曲面共形整流罩,通过在CODEV中建立扫描成像模型,研究长径比、边缘斜率、口径比以及回转中心位置对Zernike多项式中的Z4、Z5、Z8和Z9的影响规律,为共形光学系统的设计提供帮助。建立的模型中整流罩的材料为ZnS、底部直径均为120 mm,厚度均为3 mm,工作波段为4.5 μm。
2.1 长径比的影响
长径比定义了外表面顶点到底部的距离和底部口径的比值。随着长径比的增大,整流罩具有更尖的外形和更小的空气阻力。通过将不同长径比的二次曲面共形整流罩引入的波前畸变分解为Zernike多项式,得到的Zernike系数中的Z4、Z5、Z8和Z9项分别如图4~图7所示。图4~图7中整流罩边缘斜率Se=0,成像系统的口径为40 mm、旋转中心与顶点的距离z0=80 mm。

图4 不同长径比椭球型整流罩的Z4系数Fig.4 Zernike coefficient of Z4 for ellipsoid conformal domes with different aspect ratios

图5 不同长径比椭球型整流罩的Z5系数Fig.5 Zernike coefficient of Z5 for ellipsoid conformal domes with different aspect ratios

图6 不同长径比椭球型整流罩的Z8系数Fig.6 Zernike coefficient of Z8 for ellipsoid conformal domes with different aspect ratios
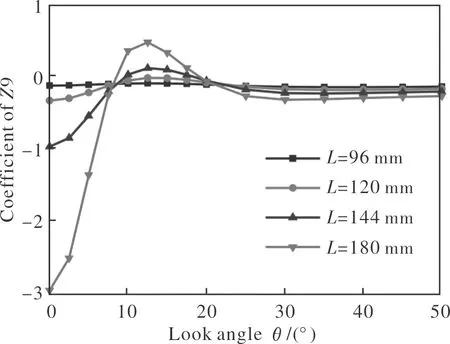
图7 不同长径比椭球型整流罩的Z9系数Fig.7 Zernike coefficient of Z9 for ellipsoid conformal domes with different aspect ratios
图4~图7表明,随着长径比的增加,椭球型共形整流罩引入的离焦像差(Z4)、像散(Z5)、彗差(Z8)和球差(Z9)的变化范围均明显增大。其中,离焦像差、彗差和球差在长径比为0.8、1.0和1.2时变化相对较小,但长径比为1.5,视角较小时急剧增加。因此,在椭球型整流罩选型时,为了有效控制引入的动态像差,整流罩的长径比在满足平台空气动力学性能时应尽量小。
2.2 边缘斜率的影响
对于二次曲面共形整流罩,即使定义了底部直径和长径比,仍然不能精确描述外表面面型。由前文分析可知,当整流罩的长度和底部直径固定时,边缘斜率决定了二次曲面的表面类型。随着边缘斜率的增加,二次曲面外表面由椭球型变为抛物面型,并最终变为双曲面型。研究表明,椭球型整流罩虽然具有引入像差小的优点,但空气阻力相对较大,不利于共形光学系统的进一步发展。因此,研究二次曲面共形整流罩引入的动态像差随边缘斜率的变化规律对共形光学系统的设计具有重要意义。图8~图11为不同边缘斜率时共形整流罩引入的主要像差随目标视场的变化曲线。其中,整流罩的长径比为1,成像系统的入瞳直径为40 mm、回转中心位置与整流罩顶点距离为80 mm。

图8 不同边缘斜率二次曲面整流罩的Z4系数Fig.8 Zernike coeficient of Z4 for quadric conformal domes with different edge slopes

图9 不同边缘斜率二次曲面整流罩的Z5系数Fig.9 Zernike coefficient of Z5 for quadric conformal domes with different edge slopes

图10 不同边缘斜率二次曲面整流罩的Z8系数Fig.10 Zernike coefficient of Z8 for quadric conformal domes with different edge slopes

图11 不同边缘斜率二次曲面整流罩的Z9系数Fig.11 Zernike coefficient of Z9 for quadric conformal domes with different edge slopes
由图8~图11可以看出,离焦像差在小视角时随边缘斜率的增加变化明显,随着视角的增大,边缘斜率的影响减小;像散和彗差在目标视场内均对边缘斜率敏感;球差在小视角时受边缘斜率影响较大。综合说来,共形整流罩引入的主要像差的变化范围随着边缘斜率的增加而增大,即抛物面形整流罩引入的像差大于椭球型整流罩,双曲面型整流罩引入的像差大于抛物面形整流罩。因此,在满足主平台空气动力学性能时,为了兼顾引入的像差大小,应选取边缘斜率较小的二次曲面共形整流罩。
2.3 口径比的影响
口径比描述了成像系统的入瞳直径与整流罩底部直径之间的关系。当整流罩底部直径一定时,增加口径比可显著增加成像系统的进光量,提高系统的探测距离。从已公开的文献可知,口径比一般为1/4~1/2。
图12~图15为不同口径比时共形整流罩引入的主要像差随目标视场的变化曲线。其中,整流罩的长径比为1、边缘斜率Se=0,回转中心位置与整流罩顶点距离为80 mm。从图12~图15中可以看出,不同口径比时各像差的变化曲线在非零视角下不相交。其中,离焦像差随着口径比的增大出现平移,变化范围稍有增加;对比长径比和边缘斜率对像散、彗差和球差的影响,可以看出随着口径比的增大,像散、彗差和球差的变化范围显著增加。因此,为了减小共形光学系统中后续校正器的设计难度,选择合理的口径比是至关重要的。

图12 不同口径比椭球型整流罩的Z4系数Fig.12 Zernike coefficient of Z4 for ellipsoid conformal domes with different aperture ratios
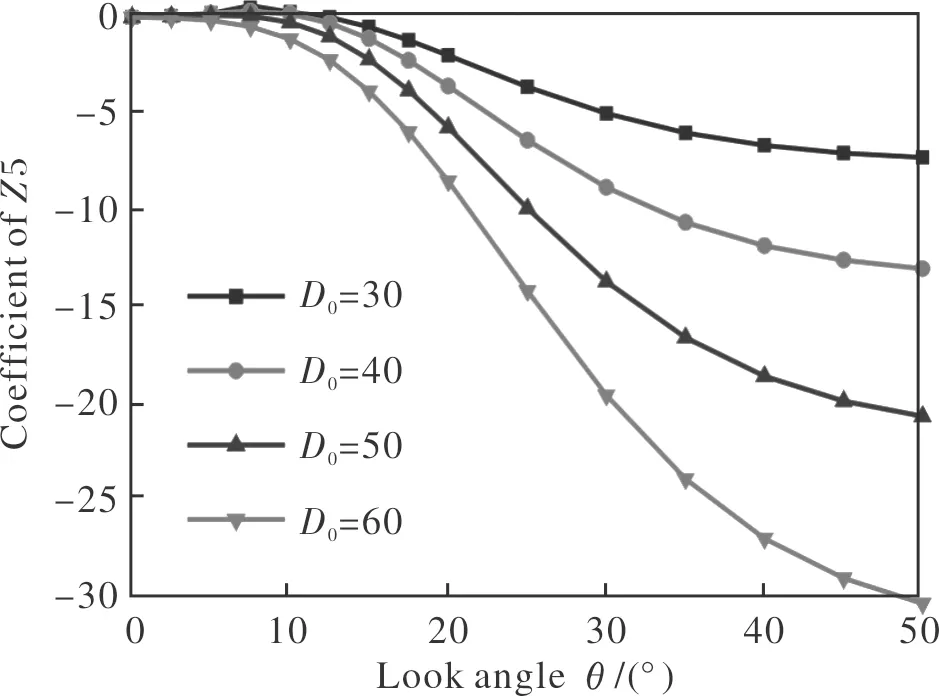
图13 不同口径比椭球型整流罩的Z5系数Fig.13 Zernike coefficient of Z5 for ellipsoid conformal domes with different aperture ratios

图14 不同口径比椭球型整流罩的Z8系数Fig.14 Zernike coefficient of Z8 for ellipsoid conformal domes with different aperture ratios
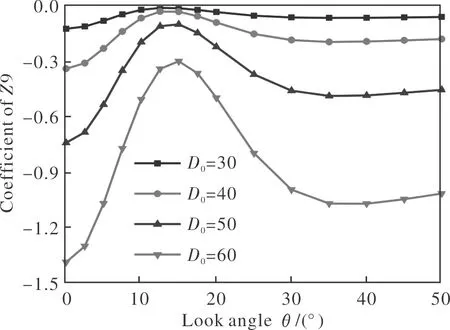
图15 不同口径比椭球型整流罩的Z9系数Fig.15 Zernike coefficient of Z9 for ellipsoid conformal domes with different aperture ratios
2.4 回转中心位置的影响
成像系统的回转中心位于整流罩的对称轴上,其位置可以用到整流罩顶点的距离描述。在传统的半球形整流罩中,成像系统的回转中心位置只能位于内外表面的球心处。在共形光学系统中,回转中心位置可根据光学设计和结构设计的需要优化选取。成像系统回转中心处于不同位置时共形整流罩引入的主要像差随目标视场的变化曲线如图16~图19所示。图16~图19中,整流罩的长径比为1、边缘斜率Se=0,成像系统的入瞳直径为40 mm。
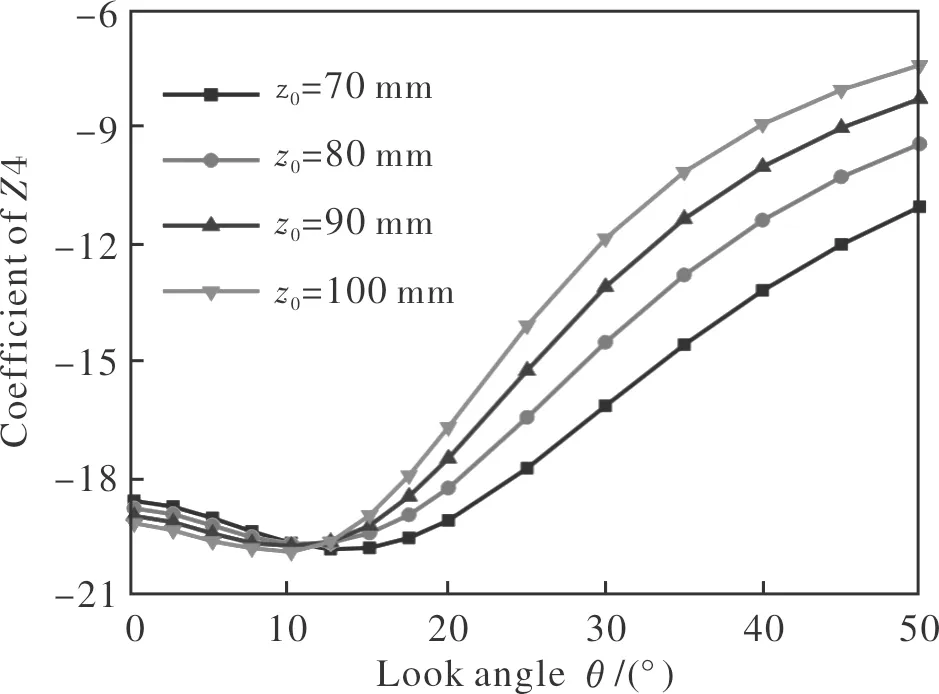
图16 不同回转中心位置时椭球型整流罩的Z4系数Fig.16 Zernike coefficient of Z4 for ellipsoid conformal domes with different position of rotation centers

图17 不同回转中心位置时椭球型整流罩的Z5系数Fig.17 Zernike coefficient of Z5 for ellipsoid conformal domes with different position of rotation centers

图18 不同回转中心位置时椭球型整流罩的Z8系数Fig.18 Zernike coefficient of Z8 for ellipsoid conformal domes with different position of rotation centers

图19 不同回转中心位置时椭球型整流罩的Z9系数Fig.19 Zernike coefficient of Z9 for ellipsoid conformal domes with different position of rotation centers
与长径比、边缘斜率以及口径比对二次曲面整流罩引入主要像差的影响不同,回转中心位置对二次曲面整流罩引入的主要像差影响较小。离焦像差、彗差和球差在视场角较小时差别很小,在大视场角时的影响也小于长径比、边缘斜率和口径比。像散在最大和最小视场角时的变化曲线几乎重合。因此,在设计二次曲面共形整流罩时,可主要根据结构需要设计回转中心位置。
3 结论
本文以二次曲面共形整流罩为研究对象,描述了其内外表面的设计方法及面型表达式。在CODEV中建立共形整流罩模型后,基于Zernike波面分解法数值仿真了不同长径比、边缘斜率、口径比和回转中心位置的共形整流罩引入的离焦像差、像散、彗差和球差。研究结果表明,口径比对二次曲面共形整流罩引入的像差影响最大。随着口径比的增加,各像差曲线不相交,变化范围增大。其次,长径比和边缘斜率对二次曲面整流罩引入的像差有较大的影响,尤其当长径比大于1.2,边缘斜率大于D/4L时,像差变化范围迅速增大。相比而言,成像系统回转中心位置对整流罩引入的像差影响最小。因此,在设计二次曲面共形光学系统时,为了降低整流罩引入的像差,尽量减小口径比、长径比和边缘斜率,而回转中心的位置可根据结构需要进行设计。
针对实际的应用,根据空气动力学的仿真结果,小长径比椭球形共形整流罩起到的气动减阻效果有限,对导弹有效射程提高的作用不明显,而大长径比双曲面型共形整流罩在气动减阻、气动热分布区域调节上的性能更为优异[17],是共形整流罩的较优选择。但设计大长径比双曲面型共形光学系统面临的设计难度更高,目前常用的固定校正板方法不易达到良好的设计效果,本文的分析结论可为设计大长径比二次曲面型共形光学系统为像差特性分析及优化提供理论支撑。

