基于双鸟群优化的高光谱图像非线性解混

翁旭辉，雷武虎，任晓东

(国防科技大学 电子对抗学院 脉冲功率激光技术国家重点实验室, 安徽 合肥 230037)

引言

高光谱遥感技术是人类对地探测的重要手段，在地质勘探，大气成分测量和军事反伪装等领域发挥着重要的作用[1]。近年来，高光谱解混成为遥感领域一个研究热点，旨在提高高光谱遥感的空间分辨率。解混技术通过提取单像元内的光谱信息来获取物质纯谱及其丰度分布，以达到亚像元分辨的目的。

线性光谱混合模型由于其简单易求解等特点，被广泛应用于解混算法中。然而，真实地物分布复杂，有些物质分布紧密，有些则具有一定的层次分布，导致高光谱相机接收到的物质反射光并非只经过一次散射，而是多次散射，这就促使学者对非线性混合模型展开研究。基于紧密型物质分布的Hapke模型、基于物质与物质之间的二次散射系数的Fan模型(fan model, FM)、广义双线性模型(generalized bilinear model, GBM)和多项式后非线性混合模型(polynomial post-nonlinear mixing model, PPNMM)都是较为典型的非线性混合模型。FM模型较为严格，考虑端元与端元之间的二次散射，其产生的虚拟端元也较多；GBM模型中假设端元不存在时，其产生的基于二次散射的虚拟端元也不存在，可有效减少虚拟端元数量；PPNMM模型包含物质自身与自身的散射,对于地物分布的特征描述更为准确具体[2]。

非线性模型具有非凸性，难以在数学推导的优化方向上进行求解。杨斌等基于双线性模型几何特性，将非线性混合项表示为一个融合了共同非线性效应的额外端点的线性贡献，将问题转化为线性解混问题[3]；在PPNMM模型下，学者提出先利用一定的先验分布(Baysian或Dirichlet)[4,5]估计模型中丰度、非线性参数以及噪声分布，再利用梯度下降(gradient, GD)来优化求解，该算法取得了较好的解混效果，但运算较为复杂，且先验分布类型对算法精度影响较大，使得GD算法在非线性场景中的应用具有一定局限性。几何特性群智能算法是通过模拟自然界中某些生物的行为而提出的一种优化算法，对于处理上述非凸性问题具有很大的优势。其典型的算法如粒子群优化算法(particle swarm optimization, PSO)[6-8]，人工蜂群优化算法(artificial bee colony optimization algorithm, ABC)[9-10]，回溯搜索算法(backtracking search algorithm, BSA)[11]，微分搜索算法(differential search, DS)[12]，樽海鞘群体算法(salp swarm algorithm, SSA)[13]等。

鸟群算法(bird swarm algorithm, BSA)通过模仿鸟类的觅食行为、警惕行为以及飞行行为而提出的一种群智能算法[14]。相比于PSO和DE[15]，该算法具有高精度，高效率和鲁棒性等优点。为克服非线性光谱混合模型中非凸性以及单个的智能群难以同时对多个参数进行迭代等问题，本文提出一种基于双鸟群优化(double bird swarm optimization algorithm, DBSOA)的高光谱图像非线性解混算法，进一步提高解混算法的精度，并设计模拟实验和光谱数据实验来检验算法的性能。

1 非线性混合模型

考虑端元之间存在非线性混合效应，端元反射光谱并非经过一次反射就进入传感器，而是与周边端元相互作用，产生非线性混合效应。假设y∈RL×1为具有L个波段的观测像元光谱，M∈RL×p为包含p中物质的光谱库，每种物质具有L个波段。a∈Rp×1表示每种物质在观测像元中所占的比例。则有：

y=gb(Ma)+n=Ma+b(Ma)⊙(Ma)+n

(1)

式中：gb表示非线性变换；⊙为Hadamard乘积，具体运算规则为

(2)

根据实际的物理意义，观测像元光谱由多种纯端元光谱组合而成，端元丰度不可能为负，且各组成端元丰度之和应为1，即a需满足和为1(abundance sum-to-one constraint, ASC)及非负性约束(abundance non-negativity constraint, ANC)，即1Ta=1和a≥0。

2 鸟群优化算法

BSA的模拟过程遵循5个原则：

1) 每只鸟都可以在警惕行为和觅食行为之间随机切换。

2) 觅食时，每只鸟都能及时记录和更新其以前的最佳经验以及鸟群以前对食物区的最佳记忆，同时个体之间保持信息共享。其数学表达式如下：

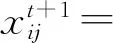
(3)

3) 当保持警惕时，每只鸟都会试图向鸟群的中心移动，但这种行为可能会受同类竞争的影响，假设食物储量较高的鸟类更可能靠近中心。

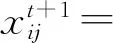
(4)

式中：k(k≠1)表示取[0,F]之间的随机数；meanj表示第j维的群平均位置。A1和A2表示影响系数。

4) 鸟类会定期飞到另一个地点。当飞向另一个地点的过程中，鸟可能经常在生产和搜索之间切换。食物储备最多的鸟是生产者，而储备最低的将是一个搜索者。其他鸟类将随机成为生产者，即有：

(5)

(6)

其中FL(FL∈[0,2])表示搜索者跟着生产者。

5) 生产者积极寻找食物，搜索者随机跟随生产者寻找食物。

3 双鸟群优化算法

3.1 优化问题

在PPNMM模型下，对高光谱图像进行逐点解混，需要求解高光谱图像中每个像素点的混合端元丰度以及非线性参数，其目标函数可以写为

(7)

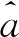
(8)

其中a满足ANC和ASC约束。

3.2 算法流程

在PPNMM模型下，通过交替迭代两个鸟群的目标函数来提高非线性混合模型下高光谱图像的解混精度。利用第一个鸟群优化迭代更新端元丰度，利用第二个鸟群优化迭代更新非线性模型中的参数，DBSOA算法具体流程如图1所示。

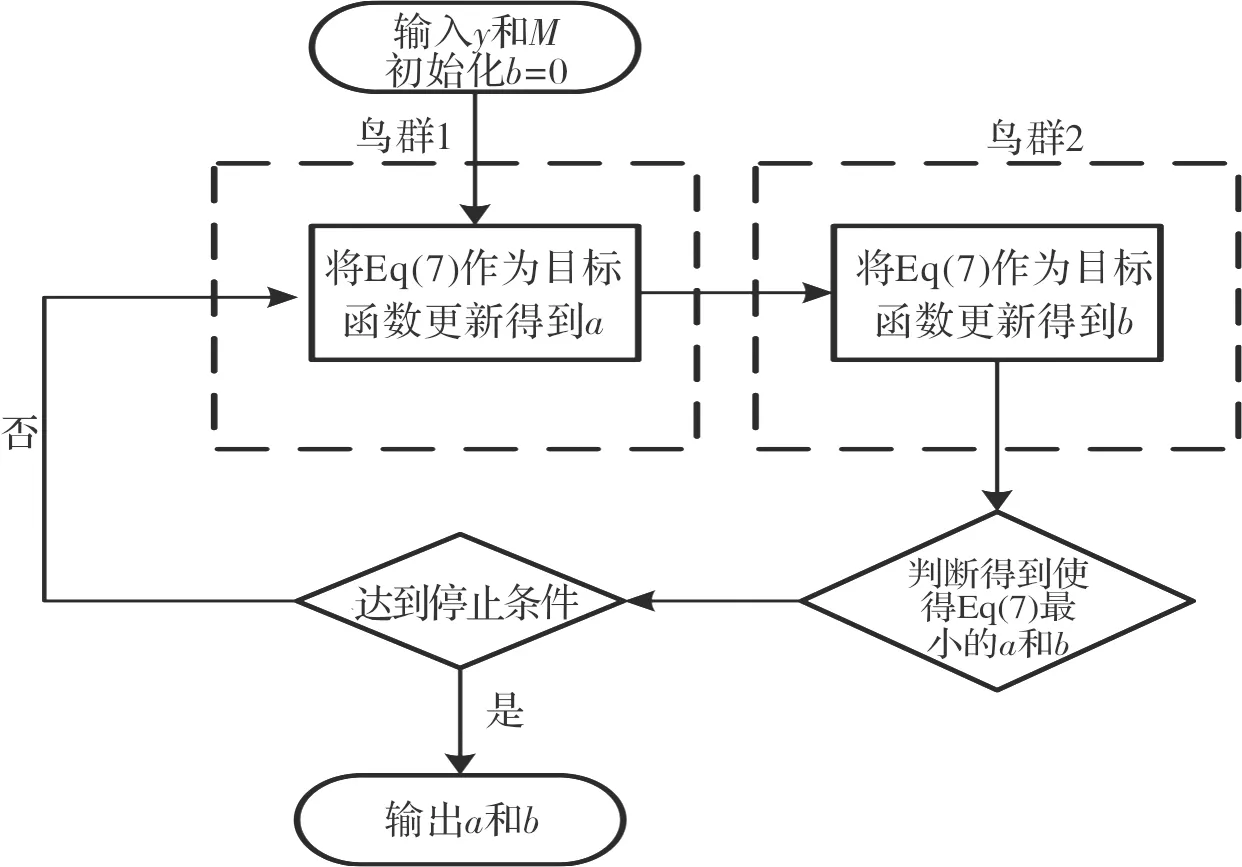
图1 DBSOA算法流程图Fig.1 Flow chart of DBSOA algorithm

算法首先初始化非线性参数b，将方程(7)作为目标函数，将b作为鸟群1的输入来更新得到丰度分布a，继而将a作为鸟群2的输入更新得到非线性参数b；最后通过判断更新得到目标函数最小的a和b值，即得到全局最优解。

参数设定是：由文献[14]可知，一般将BSA中的参数C和S设为1.5，影响因子设为1，鸟群位置更新频率设为3，种群数量选择为解维数的5至6倍。a和b的交替更新迭代以及全局最优的判断更新使得整个迭代过程形成一个闭环，每次更新只选取使得目标函数最小的a和b，保证每一次迭代收敛，最终可通过权衡算法的迭代精度以及迭代次数来设定BSA中的迭代次数。

4 实验

本节分别在仿真数据和真实高光谱数据上进行解混实验，对比FCLS[16]、SUnSAL[17]、Beyes[18-19]、GD、DBSOA等算法解混性能。性能评价指标包括丰度总均方根误差(abundance overall root mean square error, aRMSE)、平均光谱角距离(average spectral angle mapper, aSAM)和重建总均方根误差(reconstruction overall root mean square error,rRMSE)，即：

(9)

(10)

(11)

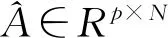
4.1 仿真实验

模拟数据集(data cube, DC)获得：从ENVI软件的光谱库中随机选择3种物质的光谱，如绿草，橄榄绿油漆，镀锌钢金属，其光谱曲线有826个波段。将它们以一定比例丰度混合，丰度系数满足ANC和ASC约束。为简化运算，设高光谱图像是20×20，共有400个像素点，利用公式(1)产生模拟高光谱数据集。

对于算法DBSOA，其中参数设置为：C和S为1.5，影响因子设为1，频率为3，迭代丰度时，种群数量设置为20，迭代非线性参数时，种群数量设置为6，交替迭代次数为40，停止条件为误差小于1e-2。

以单一像元的解混过程为例，在迭代丰度a时，模拟鸟群1 000个不同的状态时刻，随机选取前中后3个时刻的鸟群位置状态(如1,600,1 000)，其鸟群位置如图2(a)～2(c)中实心点所示，其颜色对应食物储量。由于目标函数是误差值，误差越小的实心点对应的颜色越深，表示食物储量越高，“+”表示鸟群的平均位置，“*”表示鸟群的最佳位置。从图1可以看出，总体上鸟群作无序运动，随着食物储量的变化，每只鸟不断在生产和搜索状态进行切换，但受食物和危险威胁等影响，每只鸟都向最佳位置靠拢，即越来越接近最优解。实验发现，经1 000个状态时刻变化，影响系数A1最终稳定在[0,0.37]，A2最终稳定在[0,2.7]。

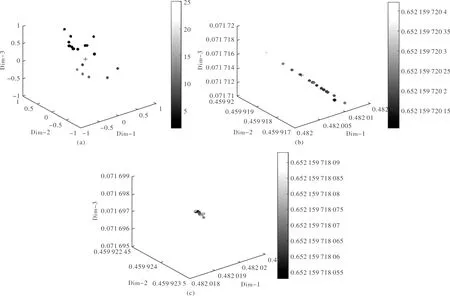
图2 不同时刻鸟群位置Fig.2 Bird flock position at different moments

图3(a)为40次迭代中鸟的最佳位置(丰度a)的变化，圆圈表示每次迭代的鸟的最佳位置，箭头为鸟可能飞行方向；图3(b)为40次迭代中b值的变化；图3(c)表示每次迭代后误差值，可以发现，随着迭代次数的增加，误差逐渐变小。

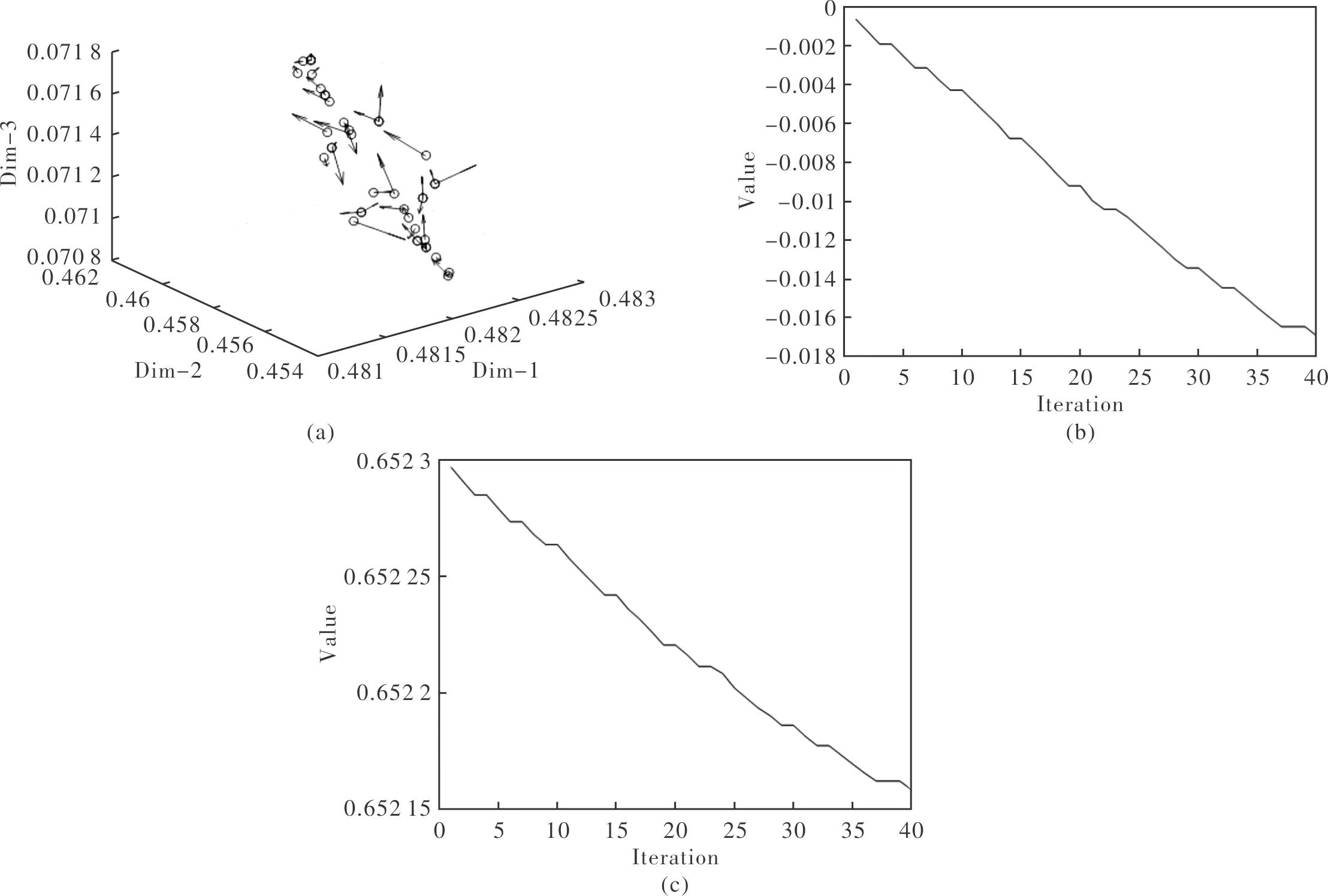
图3 迭代过程中a,b以及误差的变化Fig.3 Variation of a,b and error in each iteration

利用不同的算法分别对DC进行解混，其解混结果如图4所示。图4显示仅为端元1的丰度分布图，从图4可以看出，各个算法均能较好地对DC进行解混，为更直观地表示算法性能对比，不同算法解混结果的评价指标值如表1所示。

图4 不同算法对DC解混的结果对比Fig.4 Comparison of DC unmixing results obtained by different algorithms

表1 不同解混算法对DC解混性能对比Table 1 Comparison of DC unmixing performance with different algorithms

表1为不同算法解混结果的性能对比，各指标最优值加粗表示。通过表1可以看出，FCLS与SUnSAL性能相当，Bayes算法由于概率估计的存在，难以达到很高的精度，GD与DBSOA算法性能相当，明显好于前面3种算法。GD的重构误差比DBSOA大，虽然DBSOA在aRMSE指标上不及GD，但由于DBSOA的迭代收敛的特性，其丰度估计精度可随迭代次数的增加进一步提高。

4.2 真实光谱数据实验

本节选用Moffett数据集(http://www.ehu.es/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes)进行解混实验。该数据为1997年采集自美国加州的Moffett Filed的高光谱图。Moffett数据集具有189个波段，光谱范围为400 nm～2 500 nm，光谱分辨率为10 nm。实验选取其中50×50的子图来检验解混算法的性能，其灰度图如图5所示，主要分布有Vegetation, Water和Soil 3种物质。

图5 Moffett地区灰度图Fig.5 Grey scale map of Moffett region

利用VCA[12]对该数据集进行端元提取，构建光谱库，光谱曲线如图6所示。

图6 端元光谱库中光谱曲线Fig.6 Spectral curves in end-member spectral library

利用不同的算法分别对Moffett进行解混，解混结果如图7所示。

图7表示利用不同算法对Moffett地区光谱数据进行解混的结果来重构像元的重构误差图。从图7可以看出，GD算法的重构效果最差，DBSOA算法在水与土壤的交界处重构效果一般。

图7 不同算法对Moffett解混后像元重构误差图Fig.7 Pixel reconstruction error map of Moffett unmixing obtained by different algorithms

表2 不同解混算法对Moffett数据解混性能对比Table 2 Comparison of Moffett data unmixing performance with different algorithms

由于Moffett地区端元的真实分布未知，实验仅对比aSAM和rRMSE两项指标。通过观察表2可以看出，总体来说，DBSOA解混结果的aSAM和rRMSE两项指标均保持较低值，对比同类算法可看出，该算法对真实光谱数据解混精度较好，重构性能最好。

5 结论

文章通过模拟鸟群的觅食、警惕以及飞行等行为的群智能算法来求解非线性问题。在非线性混合模型下，通过2个鸟群的优化来交替迭代的高光谱图像像元中端元的丰度以及模型中的非线性参数，最终得到收敛的最优解。模拟实验结果表明，双鸟群优化算法具有较高的解混精度和重建效果，真实光谱数据实验证明本文提出的算法在真实高光谱图像解混中取得了较好的效果，具有广泛的应用前景。