多腔体软体驱动器负载抓持变形特性研究

涂 琴，岳东海，王延杰2，刘光新

(1.常州信息职业技术学院智能装备学院，江苏常州 213164； 2.河海大学机电工程学院，江苏常州 213022)

引言

柔性手爪是实现机器人动作柔性的重要方式，在很多领域的需求日益突出，如制造业、食品医疗行业、物流行业、电子装配、抢险救灾、海鲜抓取、水下标本采集、管道检测、空间碎片抓取、军事侦查等[1-2]。上述领域中对异形物体、柔性体、易碎物体等进行抓取时，传统的刚性手爪很难胜任。相比之下，多腔体软体驱动器具有较强的通用性[3-4]。这种结构与传统圆柱形柔性手指相比，因接触面积增大，使得承载能力和抓取稳定性增强；同时多腔体结构能够释放压力作用下手指在与轴向相垂直方向上的变形，降低材料非线性对曲率半径的影响，使得手指整体变形趋于常曲率结构，便于形态的描述与控制[5-6]。但这种变形特点很少有学者进行定量分析[7]。多腔体软体驱动器在软体机器人中应用也较广，但其变形特性与数学模型的研究较少，使其精确控制、优化设计和应用受到一定限制[8-10]。

采用多腔体软体驱动器构成柔性手爪时，由于抓取对象差异性大、材料非线性等特点，导致其结构参数差异较大，相应的设计方法和理论较为缺乏；现有的控制方法多是基于线弹性模型，与实际情况差异较大[11-13]。多腔体软体驱动器的变形特点与工作压力、负载都密切相关。但目前多腔体软体驱动器数学模型建立时，要么很少考虑负载的作用，要么考虑负载时则多基于刚体理论进行最小工作压力的推导。但由于橡胶或硅胶材料的非线性，最小工作压力很少会作为实际的控制压力[14]。相比之下，形变参数与工作范围的探讨更具实际价值。多腔体软体驱动器负载抓持解析模型建立难度较大，采用仿真方法进行分析时，会因为结构非线性、材料非线性、边界条件非线性以及流固耦合特点使得求解难度大大增加[15]。上述情况决定了采用试验的方法分析多腔体软体驱动器负载抓持时的变形特性会更加可靠，并且需建立数学模型来指导多腔体软体驱动器的设计、控制、材料选择等工作，为机器人的手眼控制等人机共融领域需求提供基础[16]。

本研究以多腔体软体驱动器构成的二指式柔性手爪为例，建立多腔体软体驱动器的形变评价指标。拟通过试验的方法分析不同工作条件下的多腔体软体驱动器变形规律，据此建立半经验的数学模型，为多腔体软体驱动器的精确控制与应用拓展提供参考。

1 材料与方法

1.1 多腔体软体驱动器结构

软体驱动器为实现弯曲，常采用柔性橡胶管加限制应变层的结构。为实现更大的弯曲角以方便抓取尺寸较小的物体，可采用多腔体软体驱动器。为提高抓取稳定性，采用如图1a所示内侧设有“V形”纹路的梯形多腔体软体驱动器，“V形”纹路高度1.5 mm，其剖面图如图1b所示。腔体为梯形结构，上底、下底、腔体高度的比值为1∶2∶4.8，充气后腔体接近圆形，如图2所示。采用梯形腔体结构而非矩形腔体是由于梯形腔体变形后的近圆形结构相对容积较大，能够最大程度上吸收驱动器的变形，从而使驱动器整体变形趋于常曲率结构，便于形态控制。当工作压力或负载变化时，多腔体软体驱动器曲率半径和腔体拟合圆会发生变化。基于该特点，建立梯形多腔体软体驱动器的形变评价指标，如图3所示。

1.橡胶 2.腔体 3.无弹性强力编织层 4.“V形”纹路图1 多腔体软体驱动器结构图

图2 软体驱动器空载下的变形

图3 软体驱动器形变评价指标示意图

1.2 多腔体软体驱动器形变评价指标

1) 末端轨迹

末端轨迹是指不同压力或负载下多腔体软体驱动器内侧末端的横向坐标lx/mm与纵向坐标ly/mm，如图3所示。末端轨迹是软体驱动器形态控制的重要依据。

2) 末端接触力

末端接触力是指由多腔体软体驱动器构成的手爪抓取物体时的单侧正压力，用F/N表示。

3) 曲率半径

多腔体软体驱动器曲率半径是指负载抓取时驱动器内侧轮廓拟合圆的半径，记为R/mm，如图3所示。采用曲率半径而非弯曲角作为多腔体软体驱动器总体形态变化的指标，一方面是考虑负载对曲率半径的正向影响关系；另一方面，对于橡胶弹性体，受气压作用柔性手指在轴线方向会有一定的伸长，对弯曲角有影响。同时，曲率半径是压力控制的直接参考指标。

4) 腔体拟合圆直径

当多腔体软体驱动器通气弯曲时，腔体由梯形演变为近圆形，如图2和图3所示。将腔体拟合圆直径作为腔体微结构的形变指标，记为di/mm，与曲率半径形成补充。腔体位于驱动器外侧，受约束较小，对受压力和负载的作用会比较敏感。由于能量守恒原理，腔体微结构的变化可能是决定多腔体软体驱动器能否实现常曲率弯曲以及形态可控性的重要因素。

1.3 试验设备

为了研究多腔体软体驱动器的变形特点，构建如图2单指空载变形特性试验台，图4a所示软体驱动器负载抓持变形试验台。图1所示多腔体软体驱动器的长度为85 mm，指根宽度均为18 mm。图2所示多腔体软体驱动器二指手爪指根间距为64 mm。对软体驱动器的接触力进行测量时，一般采用柔性传感器。但一方面柔性传感器需内嵌于多腔体软体驱动器内，制作难度较大；另一方面，由于如图1b所示多腔体软体驱动器夹持面“V”形结构的存在会使传感器的灵敏度受限。故构建如图4b所示的软体驱动器末端接触力模拟试验台，基于平面压力传感器，通过调节软体驱动器的上下位置来模拟二指手爪抓取不同直径物体时的末端接触力。图4中，采用高灵敏度200 万像素工业相机WP-GC200和配套软件Democam进行手爪变形过程的图像采集和显示。相机安装在高度可调的支架上。柔性手爪的操作台和坐标板采用加工定制。坐标板距软体驱动器中心的距离为100 mm，坐标板距相机镜头的距离为455 mm。

1.单体软体驱动器 2.控制器(含比例减压阀、换向阀)3.工业相机 4.坐标版 5.平面压力传感器6.平面压力显示 7.气动系统遥控器 8.操作台图4 软体驱动器变形特性试验台

图4中气动系统控制器进气压力0.3～0.8 MPa，输出压力-0.03～0.11 MPa。采用比例减压阀对柔性手爪的进气压力进行调节，对压力值进行实时显示。抓持对象选择以火腿肠为代表的圆柱体，以减小抓取对象特性对结果的影响，其参数如表1所示。表中 “负载一”为空载，是参照组。

表1 抓取对象结构参数

1.4 试验方法

先进行多腔体软体驱动器空载下的变形特性试验，再进行负载质量分别为30.5 g和87.5 g时的负载抓取试验。试验过程中，先分别得到多腔体软体驱动器不同负载下稳定抓持的最小压力，再线性加压，拍摄记录对应的手爪形状。根据手爪变形情况及时停止加压。末端接触力测量时，使图4b中软体驱动器指根到平面压力传感器上表面的距离满足式(1)所示的关系。并保持安装位置不变，从软体驱动器能接触到平面压力传感器开始，线性加压，模拟测量表2中不同抓取对象在不同压力下的驱动器末端接触力。采用MATLAB对Democam软件拍摄到的图片进行处理，再提取手爪变形特性参数等信息。依据图像上坐标板单位刻度和图4中相机、手爪中心、坐标板之间的间距换算得出软体驱动器变形的实际尺寸。在此基础上进行软体驱动器变形特性的分析。

H=(LS-D)/2

(1)

式中，H—— 驱动器指根到平面压力传感器上表面的距离，mm

LS—— 图4a中软体驱动器二指手爪指根间距，mm

D—— 抓取对象直径，mm

2 试验结果与讨论

2.1 多腔体软体驱动器工作特性

1) 末端轨迹

当负载质量m分别为0，30.5，87.5 g时，多腔体软体驱动器的末端轨迹坐标lx与ly随工作压力的变化规律如图5所示。从图中可以看到，空载下随着工作压力增大，末端轨迹坐标呈抛物线的趋势变化。负载的增大使驱动器的工作范围和末端轨迹变化范围均减小、线性度增加。当负载质量为30.5 g时，在工作压力为0.065 MPa附近多腔体软体驱动器的末端轨迹坐标发生突变，这是工作压力、负载、多腔体结构、超弹性材料交互作用的结果，说明了软体驱动器变形过程的复杂性。

图5 不同负载下的多腔体软体驱动器末端轨迹变化

本研究采用火腿肠作为抓持对象，在夹持力作用下会有一定变形。但一方面本研究采用的火腿肠直径与传统火腿肠相比更大、长度更短，因而相对变形更小；另一方面，与传统柔性手指的平直表面或圆柱体表面不同，图1中的多腔体软体驱动器内侧设有锯齿状“V形”纹路，抓取柔性物体时该“V形”纹路(纹路高度1.5 mm)与抓持对象的变形相补偿，使得不同负载下图3和图4中的软体驱动器内侧轮廓线与抓取对象外表面轮廓基本贴合。当考虑火腿肠表面的微变形时，主要影响图5中的手指末端横向坐标lx。对软体驱动器负载抓取变形图片的分析显示，火腿肠变形造成的多腔体软体驱动器负载抓持时手指末端横向坐标lx偏差的观测值在0.7 mm以内，与相应负载下末端横向坐标lx的比值在5%以内，说明图5的试验结果具有较强的参考价值。火腿肠是否变形，会影响软体驱动器负载抓持时的接触力，但图4中的手指末端接触力是基于试验的方法，并且是在受力平衡的状态下读取，因而能反映“V形”纹路实际抓取时受挤压的情况，使误差减小。

2) 手指末端接触力

采用图4b所示试验台模拟测试得到的多腔体软体驱动器抓取表1中不同直径物体时末端接触力F随工作压力的变化结果如图6所示。从图中看到，末端接触力总体上呈线性变化，空载下当工作压力高于0.08 MPa时，末端接触力显著增加。当负载直径增加时，末端接触力变化曲线线性度提高，且普遍左移，这是由于抓取对象直径越大，图4中软体驱动器内侧受挤压导致接触面增加，使得所需的工作压力减小。随着负载直径增加，末端接触力变化率减小，负载直径为28 mm和38 mm时的软体驱动器末端接触力差值平均值仅为0.059 N。

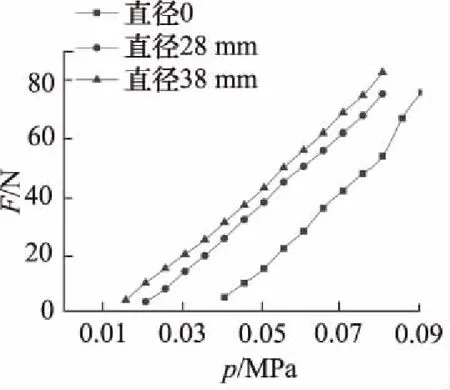
图6 不同负载末端接触力随工作压力的变化曲线

3) 不同负载下的腔体拟合圆半径

空载时多腔体软体驱动器不同压力下的各腔体拟合圆半径变化如图7所示；工作压力为0.08 MPa时，不同负载下的各腔体拟合圆半径变化如图8所示。图7表明，工作压力增大时腔体变形总体增大，并且在力

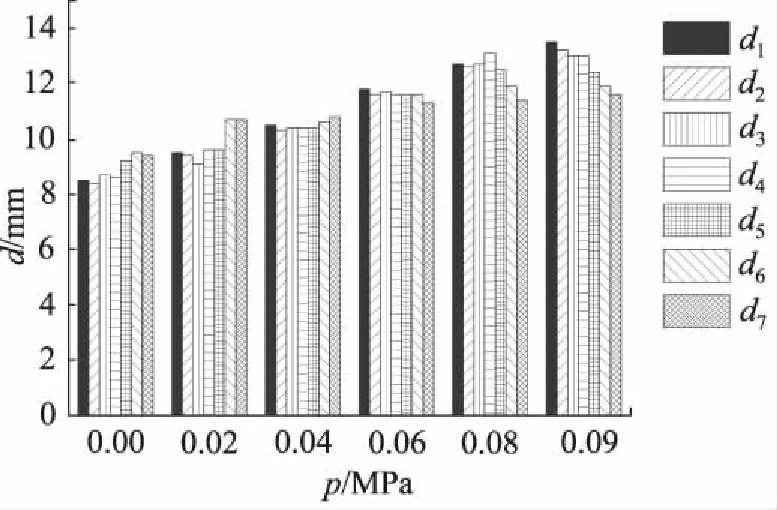
图7 空载时不同压力下的多腔体软体驱动器各腔体拟合圆半径变化

图8 工作压力为0.08 MPa时不同负载下多腔体软体驱动器各腔体拟合圆半径变化

矩作用下靠上端腔体的变形明显大于靠下端腔体的变形。图8显示，当负载增加时，手指腔体变形普遍增大，并且靠下端腔体的变形明显大于靠上端腔体的变形。这说明了多腔体软体驱动器变形规律的复杂性。

2.2 多腔体软体驱动器曲率半径变化特性分析

1) 不同负载下多腔体软体驱动器曲率半径变化规律

曲率半径反映多腔体软体驱动器的总体形态。不同负载下多腔体软体驱动器曲率半径随工作压力的变化情况如图9所示。

图9 不同负载下的多腔体软体驱动器曲率半径变化

随着工作压力增大，曲率半径呈指数下降的趋势。当负载增大，软体驱动器的工作范围和曲率半径变化范围明显减小，变形线性度提高；负载增大时，软体驱动器的工作范围普遍右移。

由表1和图9，负载三的质量是负载二质量的近3倍，但两种情况下的驱动器曲率半径差异较小，说明该结构的多腔体软体驱动器抓取稳定性较强。负载三的曲率半径随工作压力的变化很小，这就意味着，负载较大时工作压力的增大主要用于与负载力相平衡。对比图9中不同负载下软体驱动器曲率半径向右移动的幅度，可知负载的作用呈现出明显的非线性。由图5、图7、图8 和图9可以发现，工作压力和负载增大时，多腔体软体驱动器末端轨迹、腔体直径均有所变化，但曲率半径却越来越稳定，说明多腔体微结构的变形和末端轨迹的变化换来了驱动器曲率半径的稳定，可控性提高，进一步证明了多腔体软体驱动器作为可控型柔性手爪和软体驱动器组成部分的潜力。

2) 多腔体软体驱动器曲率半径数学模型建立

从图9可知，不同负载下的多腔体软体驱动器曲率半径变化趋势有较强的规律性，可以采用MATLAB数值拟合的方法逐步建立曲率半径与负载和工作压力之间的数学模型。故首先采用式(2)对3种负载质量0，30.5，87.5 g下的曲率半径随工作压力的变化曲线进行拟合，得到式(3)～式(5)。再根据得到的拟合公式，以负载为自变量对式(2)中的系数a，b进行拟合，得到统一的式(6)。

R=a×pb

(2)

式中，R—— 曲率半径，mm

p—— 工作压力，MPa

a，b—— 系数

负载一：

R=4.856×p(-0.9821)

(3)

负载二：

R=16.19×p(-0.8062)

(4)

负载三：

R=35.97×p(-0.509)

(5)

可得，多腔体软体驱动器曲率半径通用公式如下：

R=(-2.926×G2+38.79×G+4.856)×

p(0.5492×G-0.9775)

(6)

式中，G为抓取对象的重量，即负载，N。

从式(6)可以看出，负载的作用出现出明显的非线性。将拟合式(6)得到的曲率半径仿真结果与图9中的实测结果进行对比，如图10所示。从图中拟合曲线的残差可以看到，数学模型(6)的拟合精度很高。

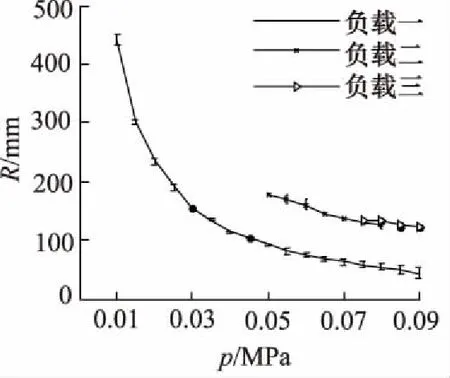
图10 曲率半径拟合结果与试验结果对比

2) 多腔体软体驱动器曲率半径变化规律预测

采用拟合式(6)对不同负载下的多腔体软体驱动器曲率半径进行预测和对比，如图11所示。

图11 不同负载下的多腔体软体驱动器曲率半径预测

从图11可以看到，负载G增大时，式(2)中的系数a发生变化，使多腔体软体驱动器曲率半径曲线的初始点先上升，再回落。且当G>0.588 N以后回落迅速，与图9中的试验结果相符。当0.588 N

图12 不同工作压力下负载对多腔体软体驱动器曲率半径的影响

从图12可以看出，多腔体软体驱动器曲率半径随负载增加先增大后急剧减小。试验测试过程及结果表明，多腔体软体驱动器通有压气体进行球形物体夹持时，由于橡胶材料的非线性和回弹能力，两侧柔性手指指尖的摩擦力会与负载经历从接触耦合力适应到稳定夹持的平衡状态。当工作压力一定，负载在低值区逐步增加时，是通过增加正压力来使摩擦力增加，以平衡负载，此时多腔体软体驱动器的弯曲角增大、曲率半径减小。此阶段橡胶回弹力的作用大于负载的作用，每次负载增加对应多腔体软体驱动器的一个平衡姿态。只有当负载达到一定数值时(图12中2种压力下此临界值均为0.68N)，负载的作用大于橡胶回弹力的作用，负载的增加才会使多腔体软体驱动器向下拉长，此时弯曲角减小、曲率增大，长度和曲率的增大使得接触面积增加，进而使摩擦力增大，以平衡负载。工作压力为0.075，0.08 MPa时多腔体软体驱动器曲率半径变化的临界负载大小相差不大，说明该值很可能主要与材料特性有关。由图11与图12，对不同重量的物体抓取时，为提高抓取稳定性和精度，需制定不同的压力控制方案，使其工作在图11中曲率半径变化曲线的线性区。

3 结论

针对多腔体软体驱动器的变形特点建立了反映驱动器末端轨迹、末端受力、整体变形、微结构变形等情况的多维度评价指标。并针对不同的运行条件设计了试验台，进行不同负载下的抓取测试，逐步建立基于数据拟合方法的多腔体软体驱动器的数学模型，为软体驱动器形态的影响因素分析和精确控制提供参考。研究结论如下：

(1) 负载的增大使多腔体软体驱动器的工作范围和末端轨迹变化范围均减小、线性度增加。工作压力对末端轨迹的作用呈现一定的非线性。末端接触力总体上呈线性变化；

(2) 多腔体软体驱动器变形后各腔体拟合圆直径随工作压力和负载变化呈现出相反的规律。工作压力增大时靠上端腔体的变形明显大于靠下端腔体的变形；当负载增加时，情况相反。腔体微结构的变形使不同工况下驱动器的曲率半径变化减小，形态可控性和抓取稳定性增强；

(3) 不同负载下多腔体软体驱动器曲率半径随工作压力增加呈指数下降的趋势。据此建立了以压力与负载为自变量的多腔体软体驱动器曲率半径数学模型，试算结果与试验结果吻合较好。负载对曲率半径的作用呈现出很强的非线性。因此，多腔体软体驱动器的负载和工作压力范围需根据实际情况合理选择。