利用三阶精度方法对气柱频率的研究

(内蒙古科技大学机械工程学院, 内蒙古包头 014010)

引言

全球工业进入高速发展阶段，使得环境问题日益加剧。对清洁能源的深入研究已经成为科研者们探寻的主要方向。对于人类赖以生存，且取之不尽用之不竭的气体研究已经成为研究的焦点。重型卡车是工业运输的血脉，以往的重型卡车多以液压作为制动媒介，如今气动制动已经在重型卡车的制动系统中占有主导地位。制动系统的好坏关系到卡车的安全性和舒适性，因此制动管路的研究就有着重要意义。

李范波等[1]通过分析阀的动作频率设计了一种气动优化程度更高的高速开关阀，也得到了阀体在气动过程中由阀产生不同脉动的开关形式。方桂花等[2]在分析管路过程中通过几种差分格式的分析对比，证明利用一阶迎风差分格式相比中心差分与二阶的Lax-Wendroff格式分析精确度更高，稳定性更强。另外通过迎风差分格式的分析也同时为紧致插值的在气动管路中的研究进行了很好的铺垫作用。权凌霄等[3]分析液压管路在随机振动下的疲劳强度，通过应力响应功率谱密度函数并利用有限元方法对管路结构危险部位疲劳寿命进行预估。ZHAO等[4-5]在分析流体运动时，基于差分格式下的紧致插值方法解双曲偏微分方程，通过圆柱绕流、堤坝实验等证明了利用紧致插值方法在流体的研究中精度更高、稳定性更好。YANG等[6]利用差分方法应用于气动管路中，并证明管路长度是影响制动时长的主要原因，其方法更加接近于真实变化。牧彬等[7]通过充气试验台对管路充气过程进行仿真通过把管路进行网格化，在时间和空间上进行差分计算，利用该研究方法得出研究管路中变量参数的理论状态解。余先锋等[8]在进行开洞结构风压实验，仿真结果表明：下流区域比例阀开口变化对管路部分影响较大，长时间充气提高管路部分的疲劳寿命。在提高管路部分研究理论依据的过程中，利用气体动力学方程的分离变量方法得出不同开口产生共振频率。吴炳胜[9]进行振动故障的诊断,并分析了出现这些振动故障的原因，提出了减小振动故障的改进措施。张振乾[10]利用ANSIS软件分析了管路的几阶振动频率，并通过差分格式利用微分变换法将气动管路进行了固有频率计算。为了避免由气动脉冲引起的管路共振，通过合理分配管路长度减小对管路部分的损害，从而提高管路寿命。黄玲璐等[11]通过对弹性梁内外共振和激励作用下稳态响应的研究，证明振动产生的破坏的最大形式是通过频率相一致导致振动所导致的。国忠金等[12]研究系统稳态下谐波在振动频率随着系统非线性项系数，利用振幅和显性系数等变化趋势，同时给出了初始振幅和非线性项系数等因素对系统振动频率响应的影响。

1 紧致插值方法

1.1 紧致插值模型介绍

紧致插值方法是模拟流体变化的一种较为成熟的算法，主要应用于流体内部交叉和流体表面变化复杂形状的界面移动问题。当遇到流体数值扩散和不稳定等问题，需要对流体网格内部信息得到更加准确的数值。于是需要大量的网格应用于计算仿真当中，然而一阶导数对于网格的分析精度较低，于是可以利用三次多项式进行插值近似。其方法所得到的都是时间和空间上的三阶精度显示稳定格式。气体作为一种特殊流体已经广泛应用于生产当中，利用精度更高的方法作为研究气体状态的依据是非常有必要的。

下面公式为气体的一般偏微分方程：

(1)

如果u是正数且为常数，则分析方法为f(t,x)=f(t-Δt,x-Δx)，这就意味着节点的值到下一个时间段的值可以通过目前时刻的值获得，下面给出一阶差分格式工作原理图。

如图1所示，其中由图1a～图1c分别是迎风差分格式在分析过程中的原理图，通过原初始波在经过uΔt后波之间的关系由点与点之间的直线连接来展示函数情况的。而图1d是紧致插值方法采用一种独特的方式，在1个网格内实现了高阶差分格式，通过利用空间网格点的变量值及其空间导数值，来描述该网格内的信息，可逼真地再现网格内的信息，函数是通过uΔt形式进行漂移的。

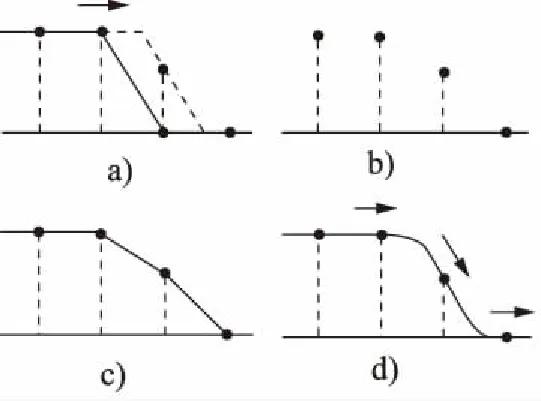
图1 紧致插值工作原理

1.2 紧致插值原理

如果所知的(x-uΔt)是在2个节点之间，那么需要通过在2节点间插值，即高精度的插值方程为：

f(x)=ai(x-xi-1)3+bi(x-xi-1)2+

(2)

上式中系数由下面方程得：

(3)

(4)

(5)

di=fi

(6)

于是可以得到下一个时间段函数值和其导数值：

(7)

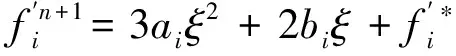
(8)

式中,ai，bi，ci，di分别表示紧致插值系数。

对于一阶迎风差分格式来说，它利用直线的方式联立相邻2个节点的信息来工作，而忽略了网格内部的信息，会引较大的数值耗散。为了真实地再现网格内部的信息，需要借助紧致插值方法对气动制动管路进行分析。

1.3 紧致插值方法下波动方程的分析

静止气体内的声速表达式为：

(9)

其中各式参数为，T为绝热温度；R为气体常数；k为绝热指数；g为重力加速度。

由连续方程和运动方程的偏微分变换整理可得脉动压力的一般偏微分方程为：

(10)

式中，p—— 压力

t—— 时间

x—— 为空间距离

通过带入相关参数，利用有限差分格将式(10)进行MATLAB数值仿真，再通过精度更高、稳定性更强的紧致插值方法与所提供基频进行数值仿真，最终通过相对误差的计算分析来判断气柱频率的振动误差。

2 数值仿真分析

2.1 有限差分波动的分析

重型卡车的一般制动压力为6.5～8.5 MPa，设进气压力为8.5 MPa，通过MATLAB软件对管路模型进行差分计算。管路距离一般为20～50 m，时间为2.5 s，时间和空间步长为100和1000。分别在20 m和50 m管路的进气口输入一个频率为1.7 Hz和4.25 Hz的余弦信号8.4 cos(3.4×π×t)和8.4 cos(8.5×π×t)作为模拟边界条件，管路下游边界条件压力均为0。利用波动方程式(10)仿真计算可得有限差分波动和频率，如图2～图5所示。

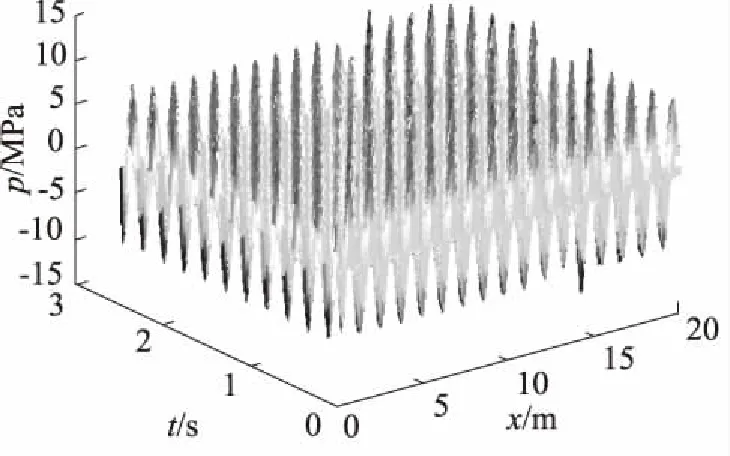
图2 20 m有限差分波动图

如图2～图5所示，通过有限差分进行仿真计算后，得到的频率图像，将该数据进行紧致插值分析有限差分方程在快速傅里叶变换后所表示的频率与振幅情况，将振幅值进行绝对值处理|x|，把所有频率所对应的振幅均描述为正方向，其便于观察曲线变化情况。利用紧致插值的方法把相关有限差分格式通过MATLAB仿真程序进行理论求解，将紧致插值原理介入波动理论解当中。

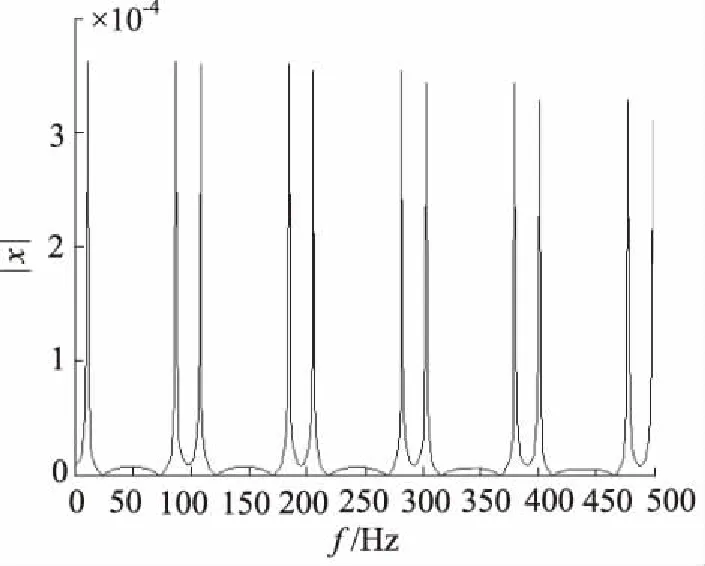
图3 20 m有限差分频率图

图4 50 m有限差分波动图

图5 50 m有限差分频率图

如图6～图9所示，紧致插值分析后频率与真实频率值完全一致，也证明了该方法在气动管路分析中的有效性。图像为了表达更清晰，在有限差分和紧致插值的过程中频率均增大25倍。通过图6～图9也可以看出紧致插值压力位移图与有限差分的耦合性良好，也证明该方法在气动研究过程中的准确性。

图6 20 m紧致插值压力位移图

图7 20 m紧致插值振动频率分析图

图9 50 m紧致插值振动频率分析图

2.2 关于频率相对误差分析

气流脉动是引起管路振动的主要原因，通过频率的相对误差δ可以更准确的分析气柱振动情况，从而避免气流脉动所引起的振动问题，如图10～图11所示。

图10 20 m相对误差频率图

图11 50 m相对误差频率图

通过对气动管路气柱频率相对误差的数学仿真，可以得出与理论计算结果频率相对误差在±0.02 Hz。

3 结论

通过对气动制动管路频率波动的研究，得到了以下结论：

(1) 由于紧致插值方法降低了差分网格内部的数值耗散，在基于有限差分分析后紧致插值算法提高了气动管路中气柱分析的精确度，通过紧致插值的压力位移图证明该方法稳定性的同时也证明了紧致插值方法研究气动的有效性；

(2) 通过对20 m和50 m频率相对误差的分析，证明无论是传统有限差分分析还是稳定性更强、精确度更高的紧致插值方法分析气动管路，计算频率相对误差为±0.02 Hz。从而为气动制动管路研究提供了有效的方法。