放慢节奏，让探究更深入*

(金华市教育局教研室，浙江 金华 321000) (衢江区第一初中，浙江 衢州 324000)

近期，在一次以“启发思考，开展深度学习”为主题的省送教活动中，一位青年教师呈现了一节“一题一课”探究学习的复习课，给同行留下了深刻的印象.该教师以新定义试题为载体，让学生围绕新定义，通过具有挑战性的问题引领，引导学生多视角地分析问题，在问题的提出、理解及解决的过程中，调动、激活以往的知识经验，加深对知识内容的理解和思想方法的把握，以融会贯通的方式对学习内容进行组织，建构出自己的知识结构，给深度学习理念下的“一题一课”更深刻的内涵.

1 试题剖析

题目如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”．

1)若△ABC是“准互余三角形”，∠C>90°，∠A=60°，则∠B=______°.

2)如图1，在Rt△ABC中，∠ACB=90°，AC=4，BC=5．若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E(异于点D)，使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．

图1 图2

3)如图2，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．

(2018年江苏省淮安市数学中考试题第26题)

此题为新定义问题，试题类比直角三角形来定义“准互余三角形”，经历阅读、理解、判断、探究、应用的过程.要求学生通过阅读理解，经历前两个问题的探究，提炼概括“准互余三角形”的特点性质，并用获得的经验来解决第3)小题，经历特殊到一般的过程，展示了一类课题学习的研究模式.

但是，试题的呈现，更多的是从评价角度考查学生的学习能力，甄别学生的学业水平.如何避免就题论题、浅层次“做练习”，需要我们为学生提供探究(如猜想、验证与应用)的空间，让学生掌握新定义的特点及其蕴含问题解决的思想方法，能够自主合理地进行思想方法的迁移，通过自主学习、协作学习和研究性学习主动进行意义建构,实现问题解决,达到深度学习.

2 教学过程

读一读如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”．你能画出一个这样的三角形吗？请标上必要的数据.

图3 图4

生1：先确定β=40°，根据40°+2α=90°，计算得到α=25°，再画出图形(如图3).

师：我们找到了通过计算画“准互余三角形”的方法.先确定一个内角40°，这样的三角形还有吗？α=50°呢？

生2：根据2×40°+β=90°，得到β=10°,因此还有“α=40°，β=10°”这种情况.

生3：当α=50°时只有图4这种情况.

说一说“准互余三角形”的两个内角α，β满足条件2α+β=90°，能够让你联想到什么三角形？类比该三角形，“准互余三角形”有什么特征？

生1：联想到直角三角形，直角三角形两锐角α，β满足α+β=90°.

生2：“准互余三角形”第3个内角是90°+α，说明它是钝角三角形.

师：根据前面的画图，可以得到什么结论？

生3：先确定一个角α画“准互余三角形”，当α<45°时，可以画出两个三角形；当45°≤α<90°时，只能画出一个三角形.

师：有没有一种特殊的“准互余三角形”？

生4：以30°为底角的等腰的“准互余三角形”.设底角为α，由2α+α=90°，求得α=30°.

生5：刚才的结论还需修改一下，当α=30°时，也只能画出一个“准互余三角形”.

师：这说明“准互余三角形”与直角三角形有着紧密的联系.

画一画你能在一个“准互余三角形”上，通过画图来体现它与一个直角三角形的联系吗？在图3、图4上尝试，说说你的发现(小组合作).

生1：如图5，AE⊥BC,可以得到∠1=25°，从而△ACE∽△BAE;如图6，BF⊥AC,∠2=25°，BC平分∠ABF.

图5 图6

师：很好，通过作三角形的高线，得到与△ABC相关联的直角三角形.通过“准互余三角形”的钝角为90°+α，你能联想到什么？

生2：把钝角分割出一个90°角.如图7，由GC⊥BC,得∠3=25°，这样△ACG∽△ABC;如图8，HC⊥AC,得到∠4=25°，△BCH是等腰三角形.

图7 图8

师：通过刚才的画图，你能得出什么结论？

生1：图5、图6可以看成在“准互余三角形”外“补形”得到直角三角形，图7、图8是“准互余三角形”内部“分割”得到直角三角形.

图9

思考(独立思考2分后呈现)画图时，你是准备直接画“准互余三角形”,还是先画相关的直角三角形？

生1：过点P作PH⊥OB于点H.如图10，作∠OPH的角平分线PQ1，得到△POQ1是“准互余三角形”.如图11，作∠Q2PH=∠O,得到△POQ2也是“准互余三角形”.

图10 图11

生2：如图10，过点Q1作Q1E⊥OA于点E.根据OH=20,得到

即

可得

生3：如图11，根据△QPH∽△OPH,得到Q2H=5,从而OQ2=15.

师：刚才画出的两个“准互余三角形”有什么共同特点，还有没有其他情况？

生4：点P是锐角顶点，应该还可以是钝角的顶点.

师：如果点P是钝角顶点，如何画出“准互余三角形”？

生5：过点P作PE⊥OA交OB于点E.如图12，在OB上取点Q作QE=EP得到点Q3;如图13，作∠QPE=∠O,就可以得到点Q4.

图12 图13

生7：如图13，根据△Q4PE∽△Q4OP,得

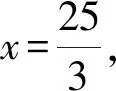
师：通过刚才的画图求解，你有什么经验？

生8：画一个“准互余三角形”，除了利用角的度数外，还可以先画一个直角三角形，由于直角顶点的不确定，需要分类讨论.

师：对，这说明“准互余三角形”的问题需要联系直角三角形，利用直角三角形有关知识求解.

算一算如图2，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．

思考1)“准互余△ABC”的内角有什么特点？与∠BCD有什么关联？

2)你准备从哪些角度进行尝试？

生1：设∠BCD=x,则

∠DBC=90°-x, ∠ABD=2x, ∠ABC=90°+x,

从前面研究可以知道，△ABC的内角∠1与∠2中必定有一个角为x,显然只有∠2=x.

生2：我是在△ABC内部分割出一个Rt△BEC,如图14，可得∠3=∠4=x,△ABE是等腰三角形.

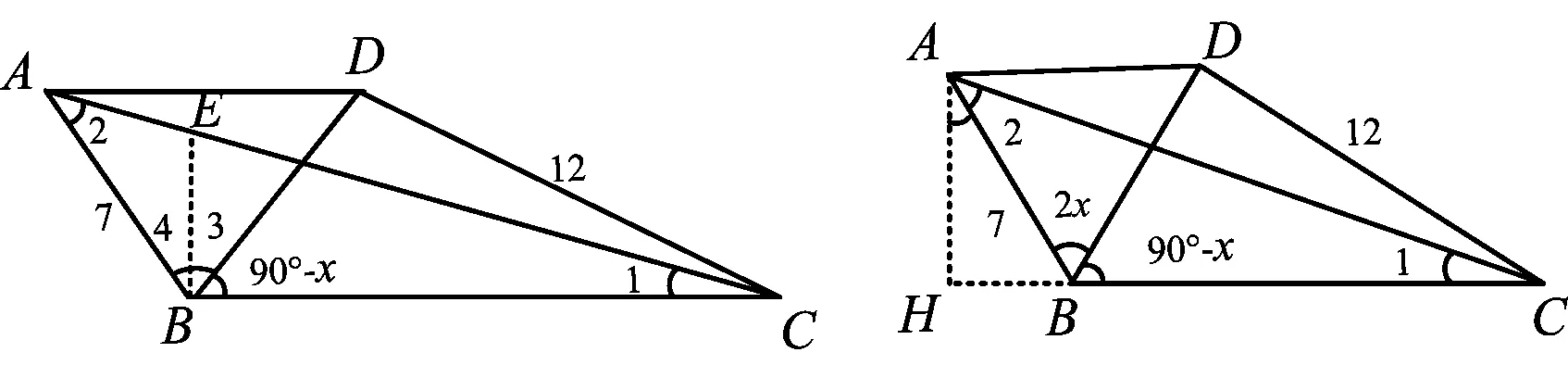
图14 图15

生3：如图15，过点A作AH⊥BC于点H，根据∠ABC=90°+∠3,可得∠3=x,由AB平分∠HAC,得△ABH∽△CBD,但接下去求解遇到困难了.

师：这时已经将△ABC的问题转化到直角三角形问题，但为什么还求不出？

生4：AB=7,DC=12，这两条边没有转化到一起.

师：怎么办？

生5：重新构造直角三角形.

图16

生6：过点C作CG⊥AB于点G，如图16，则∠4=x.

师：这也是在△ABC的外面构造直角三角形，还发现了什么？

生7：BC平分∠DCG，△BCG≌△BCD.这样可将AB=7,AC=12转化到同一个△AGC中.

生8：由∠4=∠2=x,知

△BCG∽△CAG,

可得

CG2=GB·GA,

即

122=t(t+7),

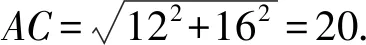
理一理“准互余三角形”有什么特点？这对求解这类问题有什么帮助？

交流后得到小结：

1)“准互余三角形”知识网络(如图17所示)；

图17

2)“准互余三角形”的问题可转化到直角三角形中解决.

3 教学反思

深度学习体现了核心素养指向的学习方式.“一题一课”是例题教学的一种形式，“小题大做”，放慢节奏，其目的就是让学生充分经历问题引导下的探究学习，通过亲身体验、深度思考和批判性思维，完成知识的自我建构，发展数学素养.

3.1 慢读细咽，达到深度理解

“如何引导学生阅读数学文本”一直困惑着我们.实现“深度阅读”的方法是学会批注、举例，举例是检验是否真正理解概念的最佳手段.在让学生阅读“准互余三角形”时，提出“你能画出一个这样的三角形吗”，放慢节奏让学生画图举例，经历阅读联想、猜想验证、画图判断的过程，从数式、形状等角度，让学生直观感受“准互余三角形”内涵，为下一步提炼“准互余三角形”性质特征打下基础，更重要的是培养学生深度阅读的能力，形成边阅读边画图、边思考的习惯.

3.2 问题引导，实现知识联系

联系已学知识，激活已有经验，培养学生的深度思维，需要学生积极地参与到每一个学习活动过程中.这就需要设置符合学生认知规律的问题系列，在一个不断进行问题提出、逐步探索、问题解决的过程中让学生体验、发现和归纳图形的特征以及解决问题的思维方法.如“说一说”提出“联想到什么三角形，‘准互余三角形’有什么特征”引导学生类比直角三角形，从数式、边、图形结构等角度来概括“准互余三角形”的特征；“找一找”中让学生思考是直接画图还是“先画相关的直角三角形”,进而再根据角的分类画出“准互余三角形”.一步步地追问，形成学生的有序思维，即通过构造直角三角形来构造“准互余三角形”，通过角的分类画出各种符合要求的三角形.到“算一算”的问题解决时，提出“准互余△ABC的内角与∠BCD有什么关联”,引导学生从已知出发，探究发现角之间的关系，让学生从不同的角度来构造直角三角形，寻求求解思路.在“理一理”时提出学习了这节课“对你求解这类问题有什么帮助”,让学生交流形成知识网络，形成概念学习的一般探究历程，形成有序思维.

3.3 试错之路，充分体验探究

探究过程中常常会碰壁或思维受阻，这时学生往往“僵住”不知所措.我们知道，有思辨才有深度，需要让学生经历“试错”过程.学生的一些不成功的方法设想、图形构造，往往被教师忽视，需要我们及时地将这些思考过程的痕迹挖掘出来，作为教学资源进一步引导观察和讨论，来进一步内化获得的经验.如“说一说”中学生得出能画出一个“准互余三角形”时α的范围有错，教师提出“有没有一种特殊情况”引导图形进行特殊化研究，让学生顿悟还有α=30°这一种情况；在“找一找”中学生画出两个∠P为锐角时的“准互余三角形”，教师停顿让学生观察角的特点，让学生自己发现∠P还可以是钝角时的“准互余三角形”；最后“算一算”将图14、图15思维受阻的过程呈现出来，作为教学资源进一步引导观察图形特点，让学生从其他角度构造直角三角形，来进一步内化获得的经验.