对一道2019年竞赛题的深入探究*

(乐从中学，广东 佛山 528315)

1 题目呈现

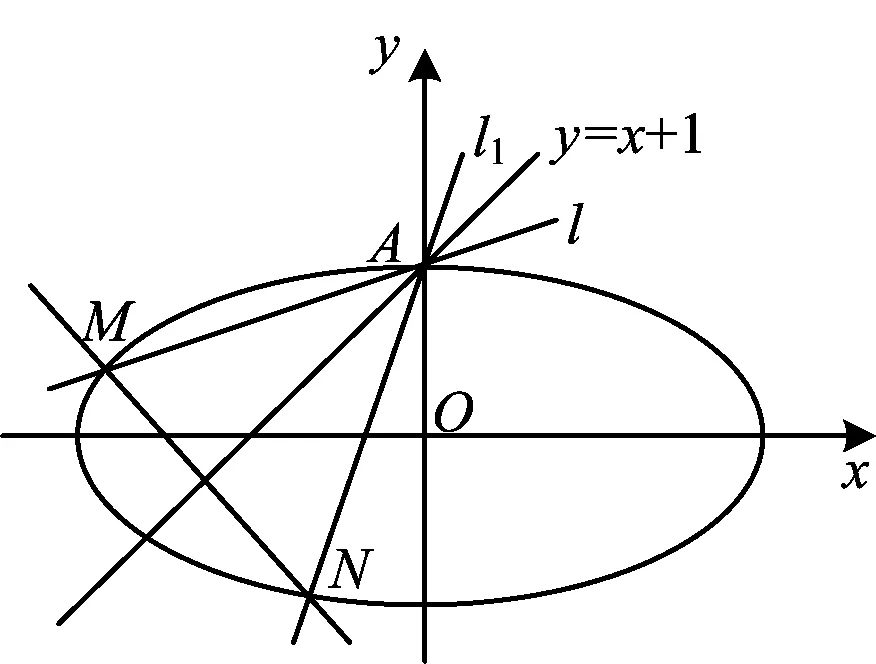
图1

1)求kk1的值；

2)求证：对任意的k，直线MN恒过定点.

(2019年全国高中数学联赛广西赛区预赛试题第12题)

2 解法探析

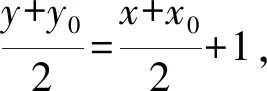
y-x=x0-y0+2,

(1)

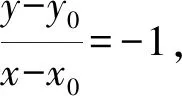
y+x=x0+y0,

(2)

x0=k(y0-1).

又点P0(x0,y0)在直线l1上，则

y0=k1x0+1，

即

y0-1=k1x0,

从而

x0=kk1x0，

由x0≠0，可得kk1=1.

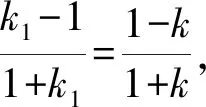
评注第1)小题中的解法2用到了到角公式，对比解法1(参考答案)，代数变形更为简单，运算量也较少.因此在竞赛中要重视方法的积累和知识的储备，熟练掌握一些有用的结论，才能缩短思维的长度，提高效率，达到事半功倍的效果.

2)证法1设M(x1,y1),N(x2,y2).由

可得

从而

同理可得

由kk1=1，可得

则直线MN的斜率为

于是直线MN的方程为

化简得

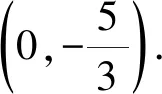
评注本证法运算量虽不小，但这是解析几何中的常用方法，这种通性通法在数学解题中有重要作用.因此在平时的教学中，教师要注重一般性的解题规律和方法(即通性通法)，要重视知识的生成过程，尽量创设问题情境引导学生探究知识，培养学生分析问题、解决问题的能力.

证法2设M(x1,y1)，N(x2,y2),因为点N(x2,y2)在椭圆E上，所以

即

由第1)小题知kk1=1，从而

化简得 4x1y2+x2y1=x2-4x1,

(3)

同理可得

即 4x2y1+x1y2=x1-4x2,

(4)

式(3)-式(4)，化简得

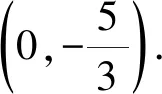
评注本证法利用斜率定义与点在椭圆上进行变换转化[1]，方法巧妙，运算量较少，但不易想到.

证法3由题意可知直线AM的方程为y=kx+1，AN的方程为y=k1x+1，则方程(kx+1-y)(k1x+1-y)=0表示直线AM,AN上的所有点，整理得

kk1x2+(k+k1)x(1-y)+(1-y)2=0.

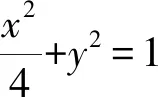
4kk1(1-y2)+(k+k1)x(1-y)+(1-y)2=0，

且y≠1，kk1=1，所以

4(1+y)+(k+k1)x+(1-y)=0,

此一次方程表示直线MN.

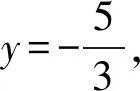
评注本证法利用直线系方程，代数变形简单，证法简捷，难点是学生较少接触这方面的知识.

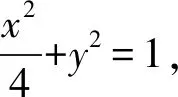
即

联立直线MN的方程，齐次化得

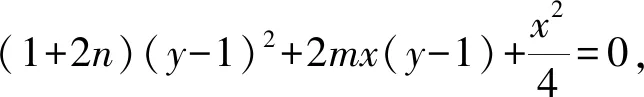
两边同除x2，得

因为kk1=1，所以

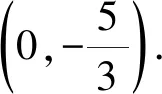
评注本证法利用齐次化方法求解，齐次化法在解决两直线斜率之和(积)相关的定值定点的圆锥曲线问题中常能达到化繁为简的效果[2].

以上4种方法从不同的角度出发思考问题，各显神通，这充分体现了试题的不拘一格：一道试题往往考查多种能力、多种思想方法；试题思维方式、解答方法不是唯一的，给考生提供了较大的发挥空间.这样通过方法的选择、解题时间的长短，甄别出考生能力的差异，达到精确区分考生的目的.

3 问题的提出

数学家波利亚曾说：“解题就像采蘑菇一样，当我们发现一个蘑菇时，它的周围可能有一个蘑菇圈.”从题目的解答过程发现，当直线l与直线l1交于椭圆的上顶点A(0,1)，且直线l，l1的斜率之积为定值1时，直线MN恒过定点.

解答完本题后，笔者思考：

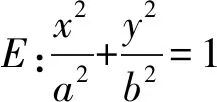
问题2在问题1中，若k1k2=λ(其中λ为常数)，则直线MN是否过定点？

问题3在问题1中，若将点A(0,b)改为椭圆上的任意一点P(x0,y0)，且k1k2=λ(其中λ为常数)，则直线MN是否过定点？

问题4在问题1中，若将点A(0,b)改为椭圆上的任意一点P(x0,y0)，且k1+k2=μ(其中μ为常数)，则直线MN是否过定点？

4 借题发挥，结论推广

通过探究，可得如下结论：

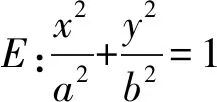
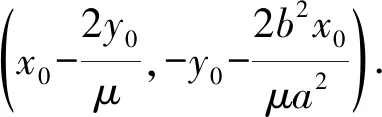
证明设直线MN的方程为

m(x-x0)+n(y-y0)=1,

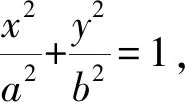
于是

即a2(y-y0)2+[2b2x0(x-x0)+

2a2y0(y-y0)]+b2(x-x0)2=0.

联立直线MN的方程，齐次化得

a2(y-y0)2+[2b2x0(x-x0)+2a2y0(y-y0)]·

[m(x-x0)+n(y-y0)]+b2(x-x0)2=0,

化简得

(a2+2na2y0)(y-y0)2+(2ma2y0+2nb2x0)(x-

x0)(y-y0)+(b2+2mb2x0)(x-x0)2=0,

两边同除以(x-x0)2，得

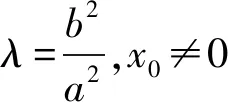
2mb2x0=2na2y0λ+a2λ-b2，

代入直线m(x-x0)+n(y-y0)=1,整理得

(2a2y0λx-2a2x0y0λ+2b2x0y-2b2x0y0)n+

(a2λ-b2)x-a2λx0-b2x0=0.

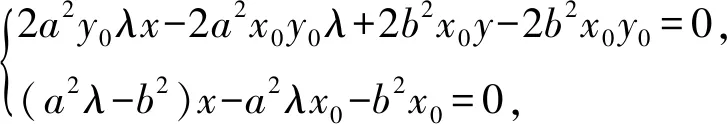
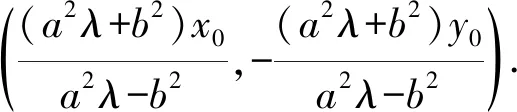
m(x-x0)+n(y-y0)=1,

化简整理得 2mb2x0+b2=(2na2y0+a2)λ,

从而

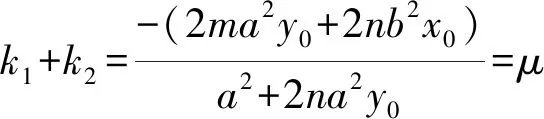
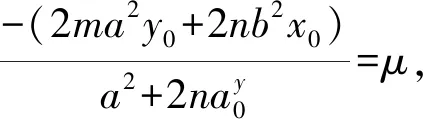
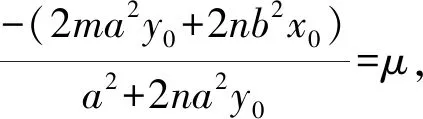
-2ma2y0=2na2y0μ+a2μ+2nb2x0，

代入直线m(x-x0)+n(y-y0)=1，整理得

由

得

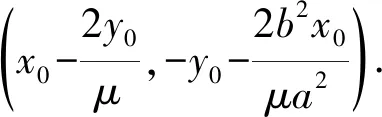
m(x-x0)+n(y-y0)=1,

得

化简整理得 2ma2y0+2nb2x0=-μ(2na2y0+a2),

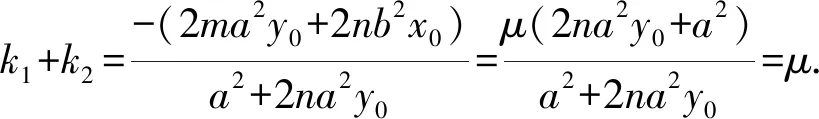
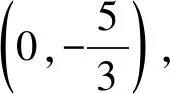
5 探究延伸，类比性质

我们知道，双曲线、抛物线与椭圆都是圆锥曲线，很多时候三者之间有可类比的性质，这体现了圆锥曲线性质的内在统一的和谐美.那么双曲线与抛物线是不是也有类似于结论1的性质呢？经探究，得到如下结论：

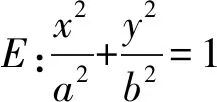
结论3过抛物线E:y2=2px(其中p>0)上的定点P(x0,y0)作斜率为k1,k2的两条直线分别与抛物线E交于点M,N.

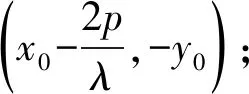
证明设直线MN的方程为

m(x-x0)+n(y-y0)=1.

由y2=2px，变形得

(y-y0+y0)2=2p(x-x0+x0)，

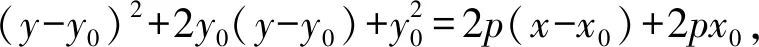
即

(y-y0)2+2y0(y-y0)-2p(x-x0)=0.

联立直线MN的方程，齐次化得

(y-y0)2+2y0(y-y0)[m(x-x0)+n(y-y0)]-

2p(x-x0)[m(x-x0)+n(y-y0)]=0,

化简得

(1+2ny0)(y-y0)2+(2my0-2pn)(x-x0)(y-y0)-

2pm(x-x0)2=0,

两边同除以(x-x0)2，得

从而

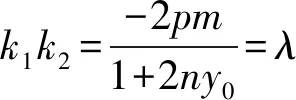
(2y0λx-2x0y0λ-2py+2py0)n+λx-λx0+2p=1.

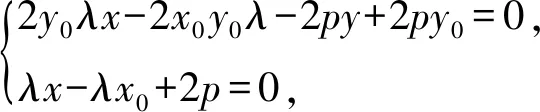
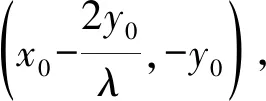
化简整理得 -2pm=λ+2nλy0=λ(1+2ny0),

于是

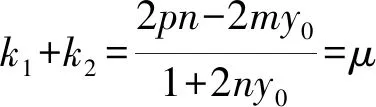
-2my0=2ny0μ-2pn+μ

代入直线m(x-x0)+n(y-y0)=1，整理得

μx-μx0+2y0=0.

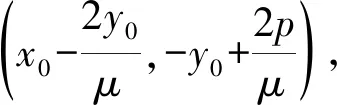
化简整理得 2pn-2my0=2ny0μ+μ=μ(2ny0+1),

于是

6 反思提升，彰显素养

圆锥曲线中的定值定点问题是高考或竞赛的热点问题之一.这类问题在考查圆锥曲线基础知识和几何性质的同时，能很好地考查学生的运算求解、推理论证等数学能力，及对方程与函数、分类讨论和转化与化归等数学思想的理解水平.在解题时要学会探索、归纳和总结，把同类型的问题进行归类，以不变应万变.

对题目进行拓展、引申探究是一名数学教师必备的专业素养，平时要重视对典型问题的深入研究，探研规律，并适当拓展，充分挖掘题目的育人价值.高中数学新课程的理念之一是倡导积极主动、勇于探索的学习方式，而学习最好的方式是发现，因此要鼓励学生通过合情推理对某些问题进行大胆地猜想，并进行探索与证明，这样的探索在数学学习中起到重要作用.教师可根据学生实际，通过探究活动，让学生体验数学的发现和创造历程，引导他们勇于发现问题、提出问题、解决问题，进而在分析、类比、猜想、证明过程中全面提高学生的综合能力，从而提升学生的数学核心素养[3].