探寻问题切入 优化解题途径*——两道立体几何联考题引发的思考

(灵璧第一中学，安徽 灵璧 234200)

1 问题提出

笔者所在学科组在高三三轮复习时，选用了各地(全国卷I考区)的联考卷(联考卷面对的对象范围广，理应具有更好的科学性与权威性).学科组教师独立思考或集思广益找到了多数难题的题源，反思试题的设计与求解，令人回味悠长，师生受益良多.但也存在着虽经多方(学科组讨论、网络求助等方式)“努力”仍无法攻克的少数“难题”.“难题”到底难在哪里？如何确定问题的切入点？试题成为难题的深层原因是什么？它反映出过往教与学的哪些不足？又当如何应对？本文以两道立体几何联考题为例，给出笔者对问题的理解及相关思考.

2 案例剖析

例1已知ABCD-A1B1C1D1为长方体，空间中到平面ACD、平面ADD1、平面CDD1、平面A1BC1距离相等的点的个数为

( )

A.1 B.4 C.5 D.无数

本题为某市2019届高三第三次教学质量检测数学(理科)试题第12题.学科组部分教师认为：类比“平面中到三角形的3条边距离相等的点有4个，分别为该三角形的1个内切圆和3个旁切圆的圆心”，推理得“空间中到三棱锥的4个面距离相等的点有5个，即该三棱锥的1个内切球和4个旁切球的球心”.由平面中最简单的封闭图形类比到空间中最简单的封闭图形具有一定的合理性，但类比推理是或然性推理，结果是否正确不得而知.还有部分教师从角平分面角度认为满足题意的点的个数为8，并用信息技术手段演示了正方体(特例)

的情况.特殊情况的结论未必适合推广到一般的情形.从特殊到一般，有时相距甚远，如本题中长方体的复杂性绝非正方体所能比拟的.结果到底如何？考虑到现行教材中已无旁切圆的概念与性质，而三维空间中(一般情形的)多个面相交的图形不够清楚直观，故笔者尝试从代数视角切入.下面给出求解过程：

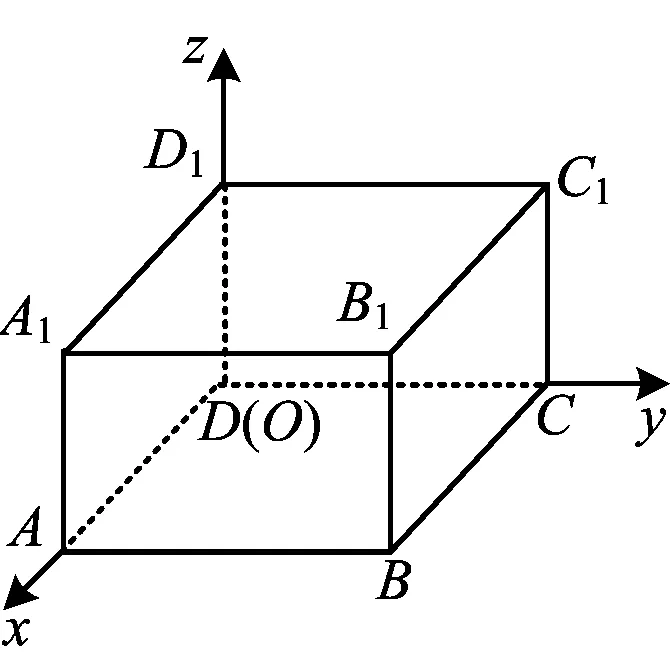
图1

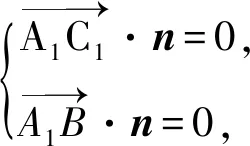
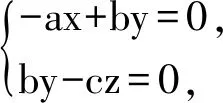
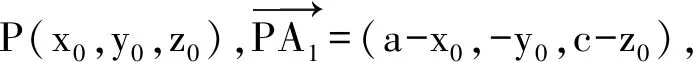
而点P到平面ACD、平面ADD1、平面CDD1的距离分别为|z0|,|y0|,|x0|.由

得

显然x0y0z0≠0.当x0=y0=z0时，整理得

此一元二次方程的判别式

Δ=4(b2c2+a2c2+a2b2)>0，

故有两组解.

当x0=y0=-z0时，整理得

当c=a+b时，

当c≠a+b时，此一元二次方程的判别式

Δ=4(b2c2+a2c2+a2b2)>0,

故有两组解.

当x0=-y0=z0时，整理得

当b=c+a时，

当b≠c+a时，此一元二次方程的判别式

Δ=4(b2c2+a2c2+a2b2)>0，

故有两组解.

当x0=-y0=-z0时，整理得

当a=b+c时，

当a≠b+c时，此一元二次方程的判别式

Δ=4(b2c2+a2c2+a2b2)>0,

故有两组解.

综上所述，在长方体中，从同一顶点出发的3条棱中，若某一棱长等于其他两条棱长之和，则满足题意的点有7个；若任一棱长都不等于其他两条棱长之和，则满足题意的点有8个.

合情推理(归纳推理、类比推理)是从已知的结论推测未知的结论，是发现一般结论的重要方式.演绎推理是由一般到特殊的推理，它常用来证明和推理数学问题，确保结论的正确性.命题组给出的答案C显然是正确类比推理过程下得到的错误结果，这表明直觉和逻辑必须齐头并进，相互为用.

图2

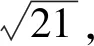
本题为某省示范联盟学校的联考数学理科试题第16题.命题组给出的解答为：

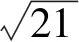
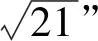
图3 图4

教师与学生的疑惑是“为什么当点P为AC的中点时，PB最大”.学科组讨论时场面冷冷清清，网络求助时也无人问津，更谈不上群策群力.可能部分教师面对学生的质疑只能照本宣科、语焉不详或环顾左右而言他.笔者给出以下解法2.

解法2如图4所示，记AB，CD的中点分别为O，E，联结OE，EA，EB.可得CD⊥AE，CD⊥BE，AE⊂平面ABE，BE⊂平面ABE，AE∩BE=E，故CD⊥平面ABE.

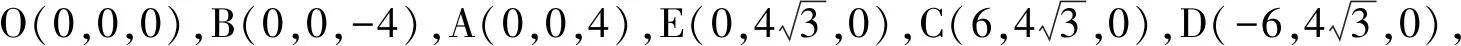
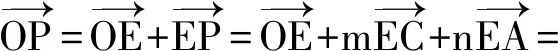
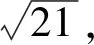
故

因为点P在侧面ACD内，所以

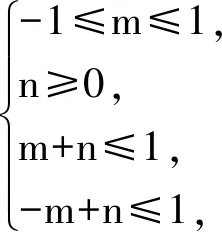
(1)

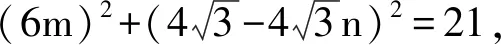
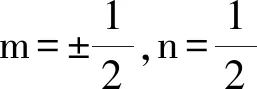
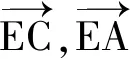
令m′=-6m,n′=8n，代入式(1)得

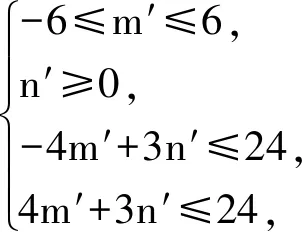
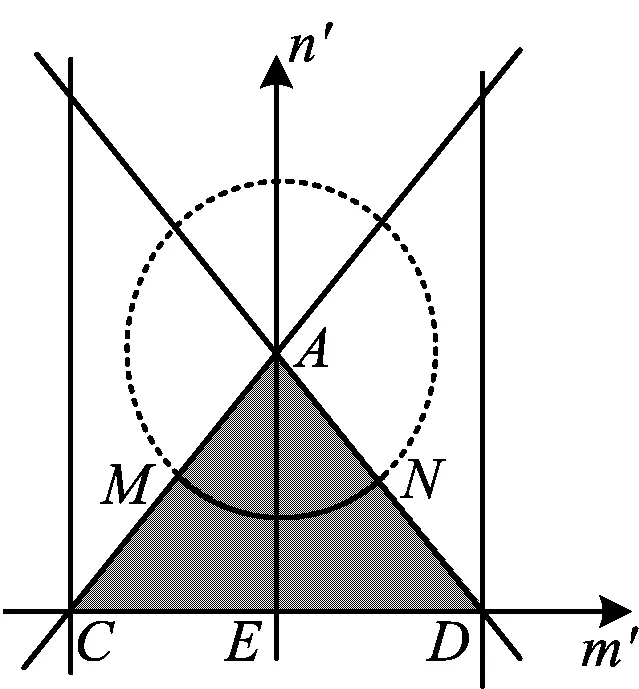
图5

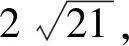
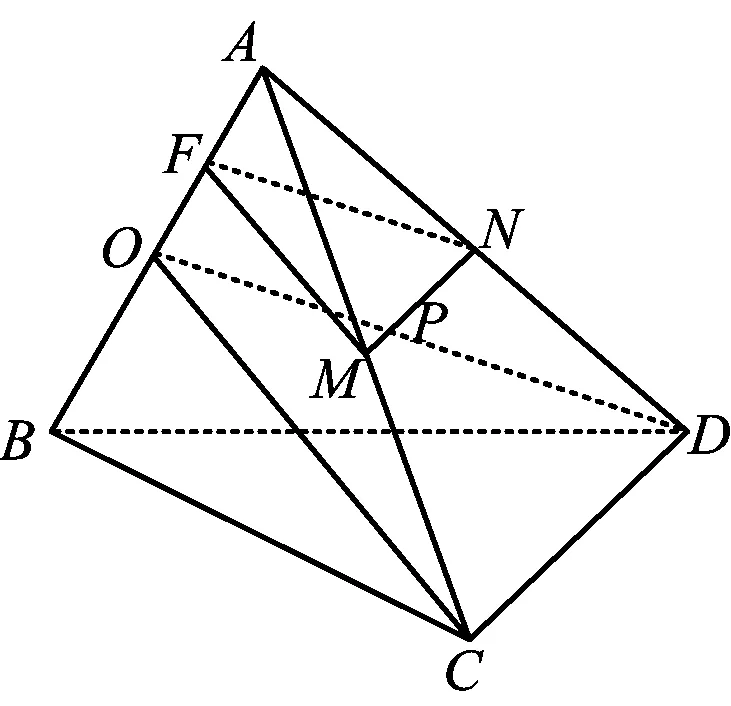
图6

部分学生误以为点P的轨迹为线段MN，直接确定点M或N满足题意，而确定轨迹为椭圆弧的学生知识更全面，可能纠结于最大值“点”的选择，思维的深刻性没有在分数上得到应有的体现，这绝不是命题者的初衷.以上学生的错解在于对点P轨迹的臆断，但其构造AB的垂面提供了点P到直线AB的距离，无疑为解题开辟了一条新的途径.解答完善如下(称为解法3)：

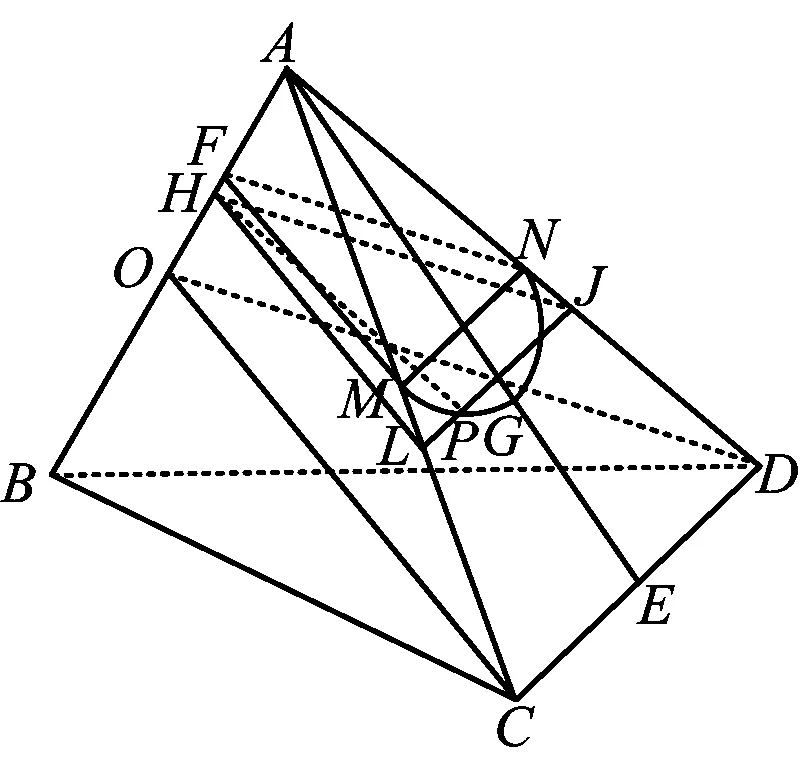
图7

3 教学思考

3.1 信息技术与数学课程要深度融合

《普通高中数学课程标准(2017年版)》中“实施建议”的第5条为“重视信息技术运用，实现信息技术与数学课程的深度融合”.具体表述为：“……在数学教学中，信息技术是学生学习和教师教学的重要辅助手段，为师生交流、生生交流、人机交流搭建了平台，为学习和教学提供了丰富的资源.”[1]“教师应注重信息技术与数学课程的深度融合，实现传统教学手段难以达到的效果.”[1]信息技术在数学教与学中的应用越来越广泛，但也存在着教学让位于技术(为技术而技术)的现象.“信息技术的一个关键特征是它运用数字、图形和符号，为抽象的数学理论构建了一个直观、动态的模型.”[2]“数学课程中使用信息技术，归根到底要聚焦在数学的关键方面：概念的定义、推理和表达、解答、解释和交流.其中，信息技术要在发现规律、获得猜想、解决问题、交流想法和展示成果等方面发挥最大的作用.”[2]

部分教师尝试利用信息技术手段探索例1与例2的结论值得肯定，无论结论如何都应该进行数学推理与证明.对于例1，学生能用向量法求出空间中的点到平面的距离(学生在学习“合情推理”中可能会遇到由“平面中的点到直线的距离公式”类比(并确认)“空间中的点到平面的距离公式”)，剩下的问题就是求解由条件得到的方程组，其中平方后提取并消去非零公共因式abc至关重要，需要学生具备较强的数感.对于例2，解法1没有表述清楚点M(AC的中点)为什么是“最大值点”，学生疑云重重；解法2构建空间直角坐标系将问题转化为求函数的值域，学生易于理解但过程略显繁琐；解法3简单明了，多数学生能够较快地理解.教师可借助信息技术手段将其直观化，引领理解困难的学生从具体到抽象.“技术不仅是工具，也是数学的一部分”已成为数学界的共识，从某种意义上讲，信息技术的运用应能促进学生的直觉思维、逻辑思维、发散思维等齐头并进，因此，信息技术与数学课程的深度融合任重而道远.

3.2 试题命制与分析评价要科学规范

试题通过考试的诊断功能为教师的教与学生的学服务.科学性是试题命制的底线，命题要立足学情，不能脱离学生实际.首先，试题的命制要体现出思维的层次性，既能贴地而行(常规解法耗时费力)又能云端跳舞(揭示本质大道至简).其次，试题还要具有一定的导向功能(如源于教材的试题能引发学生回归教材等)，引领师生始终在正确的轨道上复习备考.最后，试题的设计要具有一定的美感，通过令人向往的美召唤并感染学生，使其接受数学文化的浸润与熏陶，逐步消除其对数学不正确的认识进而深深地爱上数学.目前，多数命题者为了减少工作量往往不给出试卷中的客观题的详细解答，这也是客观题答案出错和试题脱离学生实际的重要原因.通过详尽规范地解答，命题者能对试题进行全面核查，还能通过答案的深入浅出设身处地为学生思考.例1是道错题，不满足科学性底线.例2的设计比较巧妙，但测试结果表明学生得分率过低，区分度不高(部分学生由错解得到正确答案)，命题者眼中的好题最后沦为“无效题”，原因是学生的审题能力和化归与转化能力与命题者的预设相距甚远.例2的分析与解答不能为学生提供可借鉴的思想方法，总体评价言之无物，相对空泛，没能为教师的教学指明方向，更无法提供具体落实的有力措施.

3.3 资源利用与自我剖析要准确到位

当代科学家、哲学家波普尔认为：错误中往往孕育着比正确更丰富的发现和创造因素．教师要帮助学生树立正确的错误观，坦然面对错误并及时改正与完善.例1错在何处？我们教与学中有无类似的错误？为什么教师解答没有坚持到底？教师的惰性和不自信必然会自觉或不自觉地暴露出来，进而影响学生的学习行为.对于例1，教师应引导学生认清问题根源，切实对自己的学习习惯进行深刻反思、改正、优化；对于例2，教师要给学生足够的时间和空间，让学生强化审题、聚焦重点、突破难点、思辨偶然中是否存在必然，实现知识与认知的逐步生长.