任意阶一致椭圆型算子第二特征值的上界估计

赵晓苏，钱椿林

(苏州市职业大学 数理部，江苏 苏州215104)

1 主要结果

设Ω⊆Rm是一个有界区域，Ω 的边界∂Ω 是逐片光滑的，考虑如下的特征值问题：

关于问题(1)的等式两边都是调和算子的第二特征值估计已有结果[1]，[2，[4]，[5]，问题(1)的等式左端是一致椭圆型算子，等式右端是调和算子的第二特征值估计已有结果[3]，问题(1)的等式左端是四阶一致椭圆型算子，等式右端是二阶一致椭圆型算子的第二特征值估计已有结果[6]。 问题(1)的等式左端是高阶一致椭圆型算子，等式右端是二阶一致椭圆型算子的第二特征值估计已有结果[7]。 在本文中，研究问题(1)的等式左端是任意阶一致椭圆型算子，等式右端是四阶一致椭圆型算子的第二特征值估计。 运用文献[1]中的方法，并且对其方法加以改进，对于问题(1)获得了用第一特征值来估计第二特征值的上界的不等式，其估计系数与区域的几何度量无关. 其结果在物理学和力学中有着广泛的应用，在微分方程的研究中起着重要的作用[8]。

定理 设λ1，λ2是问题(1)的两个第一、第二特征值，且0＜λ1≤λ2，则有：

2 定理的证明

设λ1是问题(1)的第一特征值，相应于λ1的特征函数为u1，简记u=u1，为简便起见，用∫替代∫Ω，且满足：

利用分部积分和(5)，得：

利用分部积分和(6)，有：

利用(2)和(7)，得：

利用(3)和(6)，有：

利用分部积分，直接计算得：

利用qk的定义和，(10)等于零，即：

从(11)知，φk与u 带权正交，且满足：。

利用Rayleigh 定理：

计算得：

结合(13)和(14)，得：

设：

利用式(15)，有：

利用(12)和(16)：

设：

引理1 设u 是问题(1)所对应第一特征值λ1的特征函数，则：

证：对于(a)，利用数学归纳法，当r=1 时，等式(a)显然成立。 假设对r=k 等式(a)也成立。

对r=k+1，利用归纳假设，得：

故有等式(a)对r=k+1 也成立，所以引理1(a)成立。

对于(b)，用数学归纳法证明，当r=1 时，利用(9)的右端，不等式显然成立。

化简整理，有：

即引理1(b)成立。

利用引理1(a)和(8)，得：

引理2 设u 是问题(1)所对应第一特征值λ1的特征函数，则

证 对于(a)，利用引理1(a)，引理1(c)，(9)的左端和Schwarz 不等式，得：

整理后引理2(a)成立：

对于(b)，利用(3)，引理1(a)和引理2(a)，有：

即引理2(b)成立。

引理3 设u 是问题(1)所对应第一特征值λ1的特征函数，则：

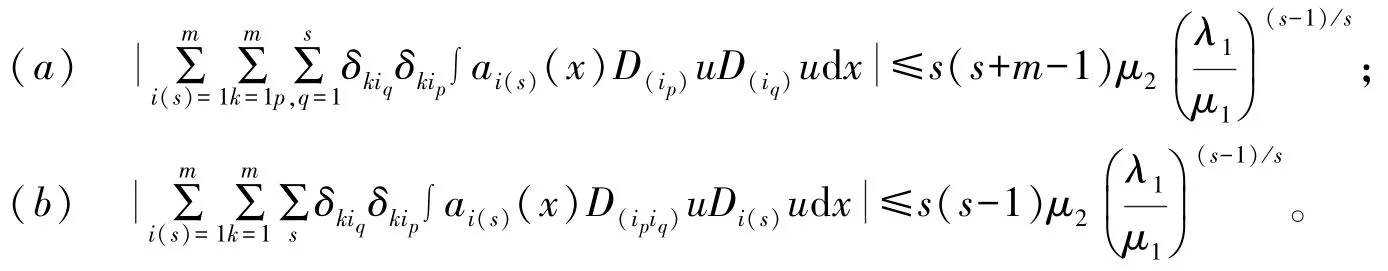
证 对于(a)，利用(2)和Schwarz 不等式，得：

当p≠q 时，利用引理2(a)和引理2(c)，取r=s-1，有：

类似地， 有：

当p=q 时，同样可得：

所以，得：

对于(b)，利用Schwarz 不等式，引理1(a) 和引理1(c)，类似地， 有：

引理4 设λ1是问题(1)的第一特征值，则：

利用分部积分，得到：

利用(19)、(20)和(21)，有：

利用(22)，引理2 和引理3，得：

引理5 对于φk与λ1(k=1，2，…，m)，有下列不等式成立：

证 利用分部积分和φk(x)=(xk-qk)u，得：

利用(23)，有：

利用(24)和(29)，有：

利用(25)、(3)、引理1(c)和Schwartz 不等式，得：

整理上式，可得引理5。

定理的证明：利用引理4 和引理5，从(27)，得到：

整理后，即得定理。