涉及差分多项式的值分布和唯一性问题*

李效敏， 于 惠

(中国海洋大学数学科学学院，山东 青岛 266100)

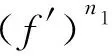
和

分别表示f的微分单项式和差分单项式，其中,b为f的小函数，n0,n1,…,nk是非负整数，η1,η2,…,ηk为k个相互判别的非零复常数，并用

γM[f]=n0+n1+…+nk

和

γM[z,f]=n0+n1+…+nk

分别表示M[f]和M(z,f)的次数，用

ΓM[f]=n0+2n1+…+(k+1)nk

表示M[f]的权。假设，M1[f],M2[f],…,Ml[f]为f的l个微分单项式，则称

P[f]=M1[f]+M2[f]+…+Ml[f]

是次数为

deg(P[f])=max{γMj[f]:1≤j≤l}，

权为

ΓP[f]=max{ΓMj[f]:1≤j≤l}

的微分多项式[3]。假设

M1(z,f),M2(z,f),…,Ml(z,f)

为f的l个差分单项式，则称

P(z,f)=M1(z,f)+M2(z,f)+…+Ml(z,f)

是次数为

deg(P(z,f))=max{γMj(z,f):1≤j≤l}

的差分多项式[4]。另外，本文还需要下述定义:

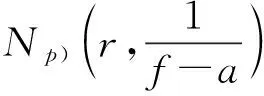
并定义

显然

0≤δk(a,f)≤δk-1(a,f)≤…≤δ2(a,f)≤δ1(a,f)=Θ(a,f)≤1。

1959年，Hayman[6]开始了亚纯函数的微分多项式的值分布理论的研究，证明了下述定理:

定理A[6]假设f是1个非常数的整函数，n≥3是1个正整数，a≠0是1个复常数，那么f′-afn取任意1个有限值无穷多次。

后来，杨重骏[7]在一定条件下研究了1类更一般的微分多项式的值分布问题，证明了下述定理：

定理B[7]假设f是1个非常数的亚纯函数，且满足

(1)

再设

是1个次数为n的微分多项式，其中Ψ(f)的每一项的次数l0+l1+…+lk≥2，并且Ψ(f)不是关于f的齐次微分多项式，那么对任意有穷复数a，我们有

近几年来，Halburd-Korhone-Tohge[8]及冯绍继与蒋翼迈[9]分别独立地建立了差分Nevanlinna理论，Laine-Yang[10]得到了涉及差分多项式的Clunie引理。应用这些理论，一些芬兰学者和中国学者开始了差分多项式的值分布理论的研究[10]和差分唯一性理论的研究[11]。

2007年，Laine-Yang[12]证明了下述定理：

定理C[12]假设f是1个非常数的亚纯函数，并且其增长级满足ρ(f)=ρ<∞。如果

那么

这里

是关于f(z)及其移动算子的差分多项式，其次数deg(G)=n为正整数，δλ,j为复常数，并且至少有1个δλ,j不等于零。

本文将利用差分Nevanlinna理论，研究1类差分多项式的值分布问题，证明了下述定理，该定理推广了定理C。

定理1 设f是1个超级小于1的非常数的亚纯函数，满足(1)，设

1997年，Lahiri[13]提出了下述问题：

问题1[13]如果2个非常数的亚纯函数的非线性微分多项式CM分担1，那么这2个亚纯函数的关系如何？

1997年，Yang-Hua[14]研究了问题1，证明了下述定理：

定理D[14]假设f与g是2个非常数的亚纯函数，n是1个正整数且满足n≥11。如果fnf′与fnf′CM分担1，那么f与g满足下述2种情形之一：

(i)f=tg,其中t是一个常数，且满足tn=1；

2002年，方明亮[15]在整函数条件下研究了问题1，证明了下述定理：

本文继续研究问题1，证明下述定理：

定理2 假设f和g是2个非常数的亚纯函数，且满足(1)和

(2)

再设

Ψ1(f)=fn(P1[f]+P2[f])，

其中，P1[f]和P2[f]是关于f的微分多项式，使得Ψ1(f)为关于f的非齐次微分多项式，其中n是正整数且满足

n>deg(P1[f])>deg(P2[f])，

这里deg(P1[f])和deg(P2[f])分别表示P1[f]和P2[f]的次数。如果Ψ1(f)与Ψ1(g)CM分担1，那么f=tg，其中t是1个常数，且满足tn+deg(P1(f))=1。

应用定理2的证明方法，由引理1和引理2可得下述定理：

定理3 假设f和g是2个有穷级非常数的亚纯函数，且满足(1)和(2)。再设

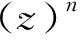
是关于f的非齐次差分多项式，其中P1(z,f)和P2(z,f)是2个差分多项式，且满足

n>deg(P1(z,f))>deg(P2(z,f))，

这里deg(P1(z,f))和deg(P2(z,f))分别表示P1(z,f)和P2(z,f)的次数。如果Ψ2(f)与Ψ2(g)CM分担1，那么f=tg，其中t是1个常数，且满足tn+deg(P1(z,f))=1。

由定理3可得下述推论：

推论1 假设f是1个非常数的有穷级亚纯函数，且满足(1)。 再设

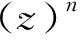
是关于f的非齐次差分多项式，其中P1(z,f)和P2(z,f)是2个差分多项式，且满足

n>deg(P1(z,f))>deg(P2(z,f))，

这里deg(P1(z,f))和deg(P2(z,f))分别表示P1(z,f)和P2(z,f)的次数。如果Ψ2(f(z))与Ψ2(f(z+η))CM分担1，其中η是一个非零复常数，那么f(z)=tf(z+η)，这里t是1个常数，且满足tn+deg(P1(z,f))=1。

1 几个引理

引理1[8]设f是1个非常数的亚纯函数，且η是一个非零复数。若f是有穷级，则对任意ε>0，存在一个线性测度有穷的集合

E=E(f,ε)⊂(0,∞)，

满足

即E的对数密度至多为ε，使得当r→∞,r∉E时，有

若f的超级

则对任意ε>0，使得当r→∞,r∉E时，有

其中，E是一个对数测度有穷的集合。

引理2[8]设T:[0,+∞)→[0,+∞)是1个非减的连续函数，s∈(0,+∞)。若T的超级小于1，即

其中，E是一个对数测度有穷的集合。

引理3[7]假设

P(f)=bnfn+bn-1fn-1+…+b2f2+b1f+b0，

(3)

其中，f是1个超越亚纯函数，b0,b1,…,bn是n+1个亚纯函数，并且满足bn≢0和

T(r,bj)=S(r,f)，0≤j≤n，

则

T(r,P(f))=nT(r,f)+S(r,f)。

引理4[1]设f是1个超越亚纯函数，且fnP(f)=Q(f)，其中，P(f)和Q(f)是f的微分多项式。如果Q(f)的次数≤n，则m(r,P(f))=S(r,f)。

注：当P(f)和Q(f)的系数b满足m(r,b)=S(r,f)时，引理4的结论也成立[1]。

引理5[14]假设F与G是2个非常数的亚纯函数，并且F与GCM分担1，那么下述情形之一成立：

(ii)FG=1；

(iii)F=G。

引理6[16]假设f是1个非常数的亚纯函数，再设

Ψ3(f)=anfn+an-1fn-1+…+a1f+a0

是关于f的n≥1次多项式，其中，an≢0，an,an-1,…,a1,a0是n+1个亚纯函数，且满足T(r,aj)=S(r,f),0≤j≤n。

如果

那么

2 定理的证明

定理1的证明：由于

所以

转化成关于f的微分多项式如下：

(4)

其中，

(5)

由于Ψ(f)是非齐次的，且每一项的次数至少是2，因此

(6)

由引理1，对于j=1,2,…,k，当r→∞,r∉E时，有

(7)

由引理2，对于j=1,2,…,k，当r→∞,r∉E时，有

(8)

因此

(9)

于是对于i=2,3,…,n，有

(10)

(11)

对任意有限复值a，设

(12)

和

(13)

将(13)代入(11)，并结合(12)，可得

g=Hk+Tk-2(H)，

(14)

其中，Tk-2(H)是H的1个微分多项式，且其次数至多是k-2。由(14)两边求导可得

g′=kHk-1H′+(Tk-2(H))′。

(15)

(16)

其中，Pk-2(H)是H和H′的1个微分多项式，其次数至多是k-2，系数a满足m(r,a)=S(r,f)。

在引理4中分别令

和

由引理4的结论可得

(17)

和

(18)

从而

(19)

同理

(20)

以下用反证法完成定理1的证明。

假设

(21)

则由(12)可知

(22)

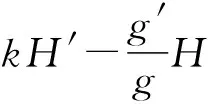
(23)

另一方面，由(21)得

(24)

(23)两边同时乘以k，可得

(25)

因此

(26)

由(14)和引理3可得

T(r,g)=kT(r,H)+S(r,H)，

因此

(27)

由(24)与(27)可得矛盾。

于是

(28)

所以

(29)

其中，c为常数。于是(14)变为

(1-c)Hk+Tk-2(H)=0。

(30)

以下分两种情形讨论:

情形1 假设c≠1，由引理4可得

m(r,(1-c)H)=S(r,H)。

(31)

由于

N(r,(1-c)H)≤N(r,f)+

S(r,f)≤S(r,f),

(32)

所以

T(r,(1-c)H)=S(r,f)。

(33)

由(13)和(33)可得矛盾。

情形2 假设c=1。首先设

g(z)=Hk(z)。

(34)

由(12)和(13)，

(35)

即

(36)

由于(36)左边是1个形如引理3中形如(3)的系数是小函数的f的多项式,因此

(37)

和

(38)

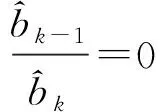
定理2的证明：首先由(1)，(2)和

Ψ1(f)=fn(P1[f]+P2[f])

可得

S(r,f)=S(r,f)

(39)

和

N2(r,Ψ1(g))=S(r,g)。

(40)

再由条件

Ψ1(f)=fn(P1[f]+P2[f])，

n>deg(P1[f])>deg(P2[f])，条件(1)和引理3可得

S(r,f)≤m(r,P1[f]+P2[f])+S(r,f)=

deg(P1[f])m(r,f)+S(r,f)。

(41)

同理，由(2)可得

S(r,g)。

(42)

由(1)，(2)和引理3可得

T(r,Ψ1(f))=T(r,fn(P1[f]+P2[f]))=

m(r,fn(P1[f]+P2[f]))+N(r,fn(P1[f]+

P2[f]))=(n+deg(P1[f]))m(r,f)+

S(r,f)。

(43)

和

T(r,Ψ1(g))=(n+deg(P1[g]))m(r,g)+

S(r,g)。

(44)

由引理5，以下分3种情形讨论：

情形1 假设Ψ1(f)Ψ1(g)≢1，并且Ψ1(f)≢Ψ1(g)，则由引理5可得

T(r,Ψ1(f))+T(r,Ψ1(g))≤

(45)

由于deg(P1[f])=deg(P1[g])，由(39)～(45)可知

(n+deg(P1[f]))(m(r,f)+

m(r,g))2deg(P1[g])m(r,f)+

2deg(P1[f])m(r,g)+S(r,f)+

S(r,g)=2deg(P1[f])(m(r,f))+m(r,g))+

S(r,f)+S(r,g),

(46)

由此可得n≤deg(P1[f])，这与条件n>deg(P1[f])矛盾。

情形2 假设Ψ1(f)Ψ1(g)=1，那么

(fn(P1[f]+P2[f]))(gn(P1[g]+P2[g]))=1。

(47)

由(47)和(2)可知

N(r,gn(P1[g]+P2[g]))≤

(n+ΓP1[f]+ΓP2[f])N(r,g)=S(r,g)。

(48)

再由Ψ1(f)Ψ1(g)=1可知，Ψ1(f)与Ψ1(g)CM分担1和-1，结合(1)和(2)可得

(n+deg(P1[f]))m(r,f)=

(n+deg(P1[f]))T(r,f)+S(r,f)=

S(r,f)≤2T(r,Ψ1(g))+S(r,f)=2m(r,Ψ1(g))+

S(r,f)+S(r,g)=2(n+deg(P1[g]))T(r,g)+

S(r,f)+S(r,g)。

(49)

和

(n+deg(P1[g]))T(r,g)+S(r,g)=

T(r,Ψ1(g))+S(r,g)≤2(n+

deg(P1[f]))T(r,f)+S(r,f)+S(r,g)。

(50)

由(49)和(50)可得S(r,g)=S(r,f)，结合(1)和(48)可得

(51)

和

P1[f]+P2[f]=an1fn1+an1-1fn1-1+…+a0，

(52)

其中

deg(P1[f])=n1≥1。

由(1)和(52)可知an1,an1-1,…,a1,a0的特征函数满足T(r,aj)=S(r,f),0≤j≤n1。

由(51)，(52)和引理6可得

(53)

N(r,1/(f+an1-1/(n1an1)))=S(r,f)。

(54)

由(1)，(54)和三密度不等式[2]可得

T(r,f)≤N(r,f)+N(r,1/f)+

N(r,1/(f+an1-1/(n1an1)))=S(r,f)，

该式表明f是1个常数，这是不可能的。

情形3 假设Ψ1(f)=Ψ1(g)，

则有

fn(P1[f]+P2[f])=gn(P1[g]+P2[g])。

(55)

设(52)，则由(52)和(55)可得

(56)

类似于情形2可得(49)和(50)。再由(1)，(2)，(49)和(50)可得