空间几何测试题A 参考答案

一、选择题

1.B 2.C 3.D 4.B 5.D 6.D

7.A 8.B 9.C 10.C 11.A 12.B

二、填空题

13.18 2π 提示:设圆锥的侧面展开图扇形的半径为R,则侧面展开图扇形的面积所以R=9。又设圆锥的底面圆半径为r,则所以r=所以圆锥的高所以该圆锥体的体积是

15.45° 提示:因为AB⊥BC,AB⊥BC1,所以∠C1BC为二面角C1-AB-C的平面角,其大小为45°。

16.26 提示:如图2,因为AB⊥CD,AD=BD,AB=10(寸),所 以AD=5(寸),在Rt△AOD中,因为OA2=OD2+AD2,所以OA2=(OA-1)2+52,所以OA=13(寸),所以圆柱底面的直径长是2AO=26(寸)。

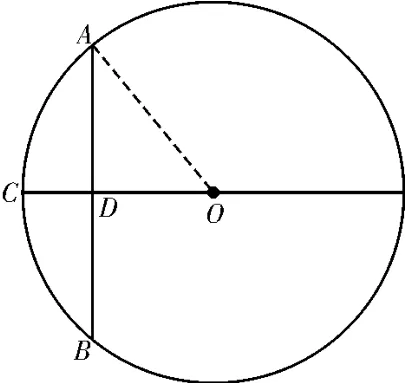
图2

三、解答题

17.由已知可得,该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥V-ABCD,如图3所示。

图3

(1)V64。

(2)该四棱锥有两个侧面VAD、VBC是全等的等腰三角形,且BC边上的高为h1=另两个侧面VAB,VCD也是全等的等腰三角形,AB边上的高为因此

18.(1)如图4,连接AC1,设AC1∩A1C=O,连接OD,在直三棱柱ABC-A1B1C1中,侧面ACC1A1是平行四边形,所以O为AC1的中点。 又因为D是棱AB的中点,所以OD∥BC1。又因为BC1⊄平面A1CD,OD⊂平面A1CD,所以BC1∥平面A1CD。

图4

(2)由(1)可知,侧面ACC1A1是平行四边形,因为AC=AA1,所以平行四边形ACC1A1是菱形,所以AC1⊥A1C。在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC,因为AB⊂平面ABC,所以AB⊥AA1。又因为AB⊥AC,AC∩AA1=A,AC⊂ 平 面ACC1A1,AA1⊂ 平 面ACC1A1,所 以AB⊥平面ACC1A1。 因为A1C⊂平面ACC1A1,所以AB⊥A1C。又因为AC1⊥A1C,AB∩AC1=A,AB⊂ 平 面ABC1,AC1⊂ 平 面ABC1,所以A1C⊥平面ABC1。因为BC1⊂平面ABC1,所以BC1⊥A1C。

19.(1)假设AE与PB共面,设平面为α,因为A∈α,B∈α,E∈α,所以平面α即为平面ABE,所以P∈平面ABE,这与P∉平面ABE矛盾,所以AE与PB是异面直线。

(2)如图5,取BC的中点F,连接EF,AF,则EF∥PB,所以∠AEF或其补角就是异面直线AE和PB所成角。

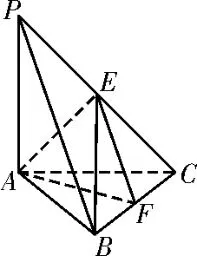
图5

因为∠BAC=60°,PA=AB=AC=2,PA⊥平面ABC,所以由余弦定理易得

所以异面直线AE和PB所成角的余弦值为

(3)因为E是PC的中点,所以E到平面ABC的距离为,所以V三棱锥A-EBC=

20.(1)因为PA⊥平面ABCD,所以PA⊥CD。又AC⊥CD,CA∩PA=A,所以CD⊥平面PAC。所以在Rt△PCD中,又在Rt△PAC中所以所以在△ACD中,AD=2,∠CAD=60°。

因为∠BCA=60°,所以在底面ABCD中,BC∥AD。 又因为AD⊂平面PAD,BC⊄平面PAD,所以BC∥平面PAD。

(2)因为点M在PB上,设

所以V三棱锥M-PCD=λV三棱锥B-PCD=λV三棱锥P-BCD解得所以点M是线段PB靠近点P的三等分点。

21.(1)因为E,F分别为AB,AC边的中点,所以EF∥BC。因为∠ABC=90°,所以EF⊥BE,EF⊥PE。又因为BE∩PE=E,所以EF⊥平面PBE。

(2)取BE的中点O,连接PO,由(1)知EF⊥平面PBE,EF⊂平面BCFE,所以平面PBE⊥平面BCFE。因为PB=BE=PE,所 以PO⊥BE。 又 因 为PO⊂平面PBE,平面PBE∩平面BCFE=BE,所以PO⊥平面BCFE。过O作OM∥BC交CF于M,分别以OB,OM,OP所在直线为x轴,y轴,z轴,建立空间直角坐标系O-xyz,如图6所示。

图6

N为线段PF上一动点,设N=(x,y,z),由得

设平面PCF的一个法向量为m=(x,y,z),则即取y=1,所以m=(-1,1,3)。

设直线BN与平面PCF所成角为θ所以直线BN与平面PCF所成角的正弦值的最大值为