解析几何测试题B

■广东信宜市教育局教研室 王位高

一、选择题

1.在正方体A1B1C1D1-ABCD中,M是侧面ABB1A1内一动点,若△MAB、△MA1D1的面积都相等,则点M的轨迹为( )。

A.线段 B.一段椭圆弧

C.双曲线的一部分D.抛物线的一部分

2.已知F1,F2分别是双曲线1(a,b＞0)的两个焦点,过其中一个焦点与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是( )。

3.已知椭圆=1(a＞b＞0),A,B是长轴的两个端点,若椭圆上存在点P,使得∠APB=120°,则该椭圆的离心率的最小值为( )。

4.在区间[-1,1]上随机取一个数k,则使直线y=k(x+3)与圆x2+y2=1相交的概率为( )。

5.如图1 所示,F(2,0)是抛物线y2=ax的焦点,点A,B分别在抛物线y2=ax和圆x2-4x+y2-12=0 的实线部分上运动,且AB总是平行于x轴,则△FAB周长的取值范围为( )。

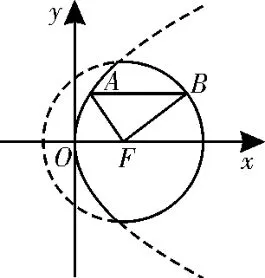
图1

A.(6,10) B.(8,12)

C.[6,8] D.[8,12]

6.《九章算术》是我国古代内容极为丰富的数学名著,第九章 “勾股”,讲述了 “勾股定理”及一些应用,还提出了一元二次方程的解法问题。直角三角形的三条边长分别称 “勾”“股”“弦”。设F是抛物线的焦点,l是该抛物线的准线,过抛物线上一点A作准线的垂线AB,垂足为B,射线AF交准线l于点C,若Rt△ABC的 “勾”|AB|=3、“股”|CB|=则抛物线方程为( )。

A.y2=2xB.y2=3x

C.y2=4xD.y2=6x

7.设P,Q分别为圆x2+(y-6)2=2和椭圆上的点,则P,Q两点间的最大距离是( )。

8.若点A的坐标为(3,2),F是抛物线y2=2x的焦点,则当点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为( )。

9.已知F为抛物线C:y2=4x的焦点,点A、B、D、E在 抛 物 线C上,AB与DE交于点F,且满足则|AB|+|DE|的最小值为( )。

A.16 B.14 C.12 D.10

10.已知椭圆=1(a＞b＞0)的左、右焦点分别为F1、F2,过点F2的直线与椭圆交于A,B两点,若△F1AB是以A为直角顶点的等腰直角三角形,则椭圆的离心率为( )。

11.已知椭圆与双曲线有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点。若C1恰好将线段AB三等分,则( )。

12.如 图2,F1、F2分 别是双曲线＞0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M。若|MF2|=|F1F2|,则C的离心率是( )。

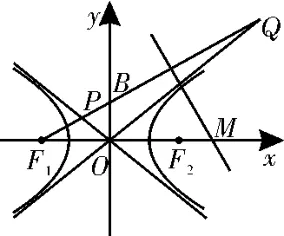
图2

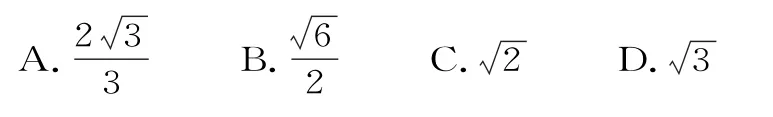
二、填空题

13.一个椭圆中心在原点,焦点F1,F2在x轴上是椭圆上一点,且|PF1|,|F1F2|,|PF2|成等差数列,则椭圆方程为_____。

14.已知抛物线C:x2=4y,任意直线l:y=kx+b(b≠0),已知直线l交抛物线C于M,N两点,P为y轴上一点且满足∠OPM=∠OPN(O为坐标原点),则P点的坐标为_____。

15.已知椭圆=1(a1＞b1＞0)与双曲线=1(a2＞0,b2＞0)有公共的左、右焦点F1、F2,它们在第一象限交于点P,其离心率分别为e1,e2,以线段F1F2为直径的圆恰好过点P,则=____。

16.已知双曲线上的一点到双曲线的左、右焦点的距离之差为4,若抛物线y=ax2上的两点A(x1,y1),B(x2,y2)关于直线y=x+m对称,且x1x2,则m的值为____。

三、解答题

17.已知P是椭圆b＞0)上一点,P到椭圆C的两个焦点F1,F2的距离之和为

(1)求椭圆C的方程和离心率。

(2)设直线y=kx+2交椭圆于M,N两点,是否存在实数k,使以MN为直径的圆过点F(-1,0)? 若存在,求出k的值;若不存在,请说明理由。

18.在平面直角坐标系xOy中,已知平行于x轴的动直线l交抛物线C:y2=4x于点P,F为C的焦点。圆心不在y轴上的圆M与直线l,PF,x轴都相切,设圆心M的轨迹为曲线E。

(1)求曲线E的方程。

(2)若直线l1与曲线E相切于点Q(s,t),过Q且垂直于l1的直线为l2,直线l1,l2分别与y轴相交于点A,B。当线段AB的长度最小时,求s的值。

19.已知椭圆的离心率直线x=t(t＞0)与曲线E交于不同的两点M,N,以线段MN为直径作圆C,圆心为C。

(1)求椭圆E的方程;

(2)若圆C与y轴相交于不同的两点A,B,求△ABC的面积的最大值。

20.已知双曲线的左、右顶点分别为A1、A2,P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点。

(Ⅰ)求直线A1P与A2Q交点的轨迹E的方程;

(Ⅱ)若过点H(0,h)(h＞1)的两条直线l1和l2与轨迹E都只有一个交点,且l1⊥l2,求h的值。

21.已知点F(1,0),A是直线l1:x=-1上的动点,过A作直线l2,l1⊥l2,线段AF的垂直平分线与l2交于点P。

(1)求点P的轨迹C的方程;

(2)若M,N是直线l1上两个不同的点,且△PMN的内切圆方程为x2+y2=1,直线PF的斜率为k,求的取值范围。