解析几何测试题A

■广东信宜中学 邓小雁

一、选择题

1.已知线段AB的垂直平分线为y=2x,其中点A的坐标为(0,1),则点B与圆O:x2+y2=1的位置关系是( )。

A.点B在圆O内 B.点B在圆O上

C.点B在圆O外 D.点B不能确定

2.以直线为渐近线的双曲线的离心率为( )。

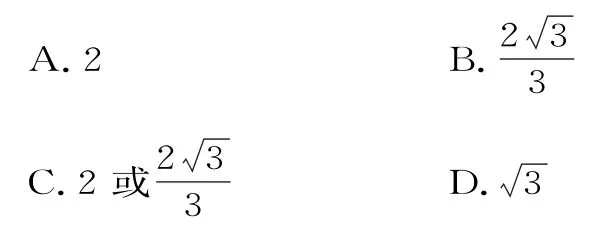
3.若一个椭圆的长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )。

4.已知椭圆与双曲线的焦点相同,则双曲线的离心率为( )。

5.已知角α的顶点与坐标原点重合,始边与x轴正半轴重合,终边经过点a),若点A在抛物线的准线上,则sinα=( )。

6.在同一直角坐标系中,曲线与抛物线y2=x的交点横坐标所在的区间为( )。

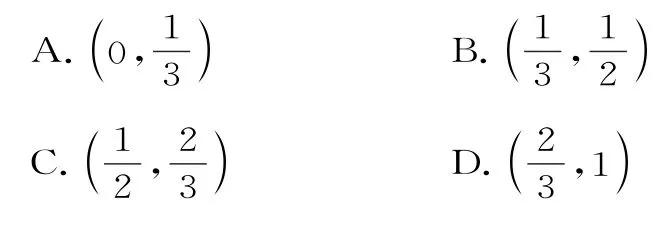
7.过抛物线C:y2=2px(p＞0)的焦点F的直线l与抛物线交于M,N两点,若则直线l的斜率为( )。

8.若动圆的圆心在抛物线上,且与直线y+3=0相切,则此圆恒过的定点是( )。

A.(0,2) B.(0,-3)

C.(0,3) D.(0,6)

9.已知抛物线的焦点F也是椭圆的焦点,记C1与C2在第一象限内的交点为A,且则椭圆的离心率为( )。

10.已知双曲线的右焦点为F,P为双曲线左支上一点,点则△APF周长的最小值为( )。

11.已设F1,F2分别是椭圆=1(a＞b＞0)的左焦点和右焦点,点P在椭圆C上,若线段PF1的中点在y轴上,∠PF1F2=30°,则椭圆的离心率为( )。

12.在直角坐标系xOy中,抛物线C:y2=4x的焦点为F,准线为l,P为C上一点,PQ垂直l于点Q,M,N分别为PQ,PF的中点,直线MN与x轴交于点R,若∠NFR=60°,则NR=( )。

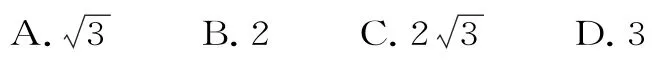
二、填空题

13.若直线2ax-by+2=0(a＞0,b＞0)经过圆x2+y2+2x-4y+1=0 的圆心,则的最小值为_____。

14.在平面直角坐标系xOy中,已知点A,F分别为椭圆的右顶点和右焦点,过坐标原点O的直线交椭圆C于P,Q两点,线段AP的中点为M,若Q,F,M三点共线,则椭圆C的离心率为_____。

15.直线l过抛物线C:x2=4y的焦点F,且与抛_物线C交于A,B两点,O为原点,则

16.已知点A(a,0),P是双曲线y2=1右支上任意一点,若|PA|的最小值为3,则a=____。

三、解答题

17.已知抛物线y2=2px(p＞0)的焦点为直线2x+y-1=0与x轴的交点,O为坐标原点。

(1)求抛物线的方程;

(2)若过点A(2,0)的直线l与抛物线相交于B,C两点,求证

18.已知椭圆的一个焦点与抛物线C2:y2=2px(p＞0)的焦点F重合,且点F到直线x-y+1=0的距离为C1与C2的公共弦长为

(1)求F的坐标;

(2)求椭圆C1的方程。

19.为了考察冰川的融化状况,一支科考队在某冰川上相距8 km 的A,B两点各建一个科考基地。视冰川面为平面形,以过A,B两点的直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系(如图1)。考察范围为到A,B两点的距离之和不超过10 km 的区域。

(1)求考察区域边界曲线的方程。

(2)设线段P1P2是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2 km,以后每一年移动的距离是前一年的2 倍。问:经过多长时间,点A恰好在冰川边界线上?

图1

20.已知抛物线C:y2=2px(p＞0)的焦点为F,M为抛物线C上一点,|MF|=8,且为坐标原点)。

(1)求抛物线C的方程;

(2)过点F的直线l与抛物线C交于A,B两点,求△AOB面积的最小值。

21.已知是椭圆1(a＞b＞0)上的一点,F1,F2是椭圆C的两个焦点,且满足|AF1|+|AF2|=4。

(1)求椭圆E的方程;