空间几何测试题A

■湖北省巴东县第三高级中学 田煌英

一、选择题

1.棱柱的侧面都是( )。

A.三角形 B.四边形

C.五边形 D.矩形

2.已知向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )。

A.a∥b,a∥cB.a∥b,a⊥c

C.a∥c,a⊥bD.以上都不对

3.如图1是一个物体的三视图,则此三视图所描述的几何体是图2中的( )。

图1

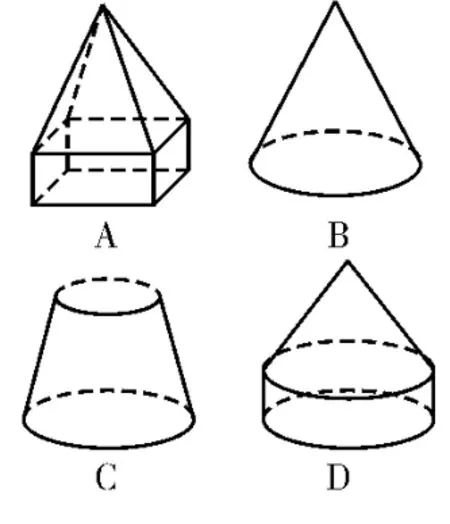
图2

4.已知一个简单几何体的三视图如图3所示,若该几何体的体积为24π+48,则r的值为( )。

图3

A.1 B.2

C.3 D.4

5.图4所示的4个图形均表示两个相交平面,其中画法正确的是( )。

图4

6.下列说法错误的是( )。

A.垂直于同一个平面的两条直线平行

B.若两个平面垂直,则其中一个平面内垂直于这两个平面交线的直线与另一个平面垂直

C.一个平面内的两条相交直线均与另一个平面平行,则这两个平面平行

D.一条直线与一个平面内的无数条直线垂直,则这条直线和这个平面垂直

7.如图5 所示,在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的 交 点。 若则下列向量中与相等的向量是( )。

图5

8.如图6,网格纸上小正方形的边长为a,粗实线画出的是某几何体的三视图,若该几何体的表面积为则a的值为( )。

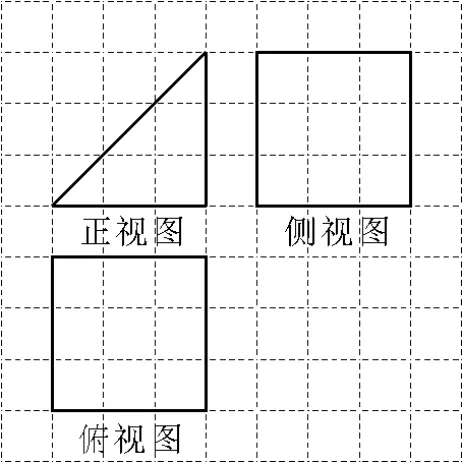
图6

9.将图7中的等腰直角三角形ABC沿斜边BC上的中线折起得到空间四面体ABCD(如图8),则在空间四面体ABCD中,AD与BC的位置关系是( )。

图7

图8

A.相交且垂直

B.相交但不垂直C.异面且垂直

D.异面但不垂直

10.若平面α,β的法向量分别为n1=(2,-3,5),n2=(-3,1,-4),则( )。

A.α∥β

B.α⊥β

C.α,β相交但不垂直

D.以上均不正确

11.如图9所示,体积为8的正方体ABCD-A1B1C1D1中,分别过点A1,C1,B作A1M,C1N,BP垂直于平面ACD1,垂足分别为M,N,P,则六边形D1MAPCN的面积为( )。

图9

12.如图10,在三棱锥D-ABC中,AC=BD,且AC⊥BD,E,F分别是棱DC,AB的 中 点,则EF和AC所成的角等于( )。

图10

A.30° B.45°

C.60° D.90°

二、填空题

13.某圆锥体的侧面展开图是圆心角为的扇形,当侧面积是27π时,则该圆锥体的体积是_____。

14.已知正四棱锥P-ABCD的底面边长为2,表面积为12,则它的体积为____。

15.如图11 所示,在正方体ABCD-A1B1C1D1中,截面C1D1AB与底面ABCD所成二面角C1-AB-C的大小为_____。

图11

16.“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小。以锯锯之,深一寸,锯道长一尺。问径几何。”用现在的数学语言表述是:“如图12所示,一圆柱形埋在墙壁中,AB=1尺,D为AB的中点,AB⊥CD,CD=1 寸,则圆柱底面的直径长是____寸。”(注:1尺=10寸)

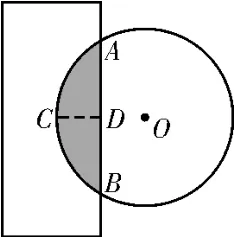
图12

三、解答题

17.已知某几何体的俯视图是如图13所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4 的等腰三角形。

图13

(1)求该几何体的体积V;

(2)求该几何体的侧面积S。

18.如图14 所示,在直三棱 柱ABC-A1B1C1中,AB⊥AC,AC=AA1,D是 棱AB的中点。求证:

图14

(1)BC1∥平面A1CD;

(2)BC1⊥A1C。

19.如图15 所示,在三棱锥P-ABC中,PA⊥ 平 面ABC,∠BAC=60°,PA=AB=AC=2,E是PC的中点。

图15

(1)求证:AE与PB是异面直线;

(2)求异面直线AE和PB所成角的余弦值;

(3)求三棱锥A-EBC的体积。

20.如图16 所示,在四棱锥P-ABCD中,已知PA⊥平面ABCD,△ABC为等边三角形,PA=2AB=2,AC⊥CD,PD与平面PAC所成角的正切值为

图16

(1)证明:BC∥平面PAD;

(2)若M为PB上一点,且V三棱锥M-PCD=试判断点M的位置。21.如图17,在△ABC中,AB=BC=2,∠ABC=90°,E,F分别为AB,AC边的中点,以EF为折痕把△AEF折起,使点A到达点P的位置,且PB=BE,如图18所示。

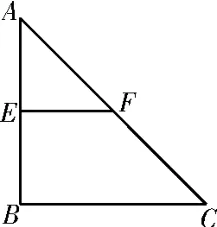
图17

图18

(1)证明:EF⊥平面PBE;

(2)设N为线段PF上的动点,求直线BN与平面PCF所成角的正弦值的最大值。