空间几何测试题B 参考答案

一、选择题

1.C 2.D 3.B 4.A 5.A 6.D

7.D 8.A 9.B 10.D 11.D 12.D

二、填空题

14.②③④

15.3

16.(0,12π] 提示:由题意知,当1＜时,交线为6个圆且半径均为总弧长最大为12π;当时,交线为24段相等的弧,设每段弧所对的圆心角为所以即则记各弧所在圆的半径R=则总弧长为l(θ)=24R·2θ=而l′(θ) = 48 ·所以l′(θ)＞0,所以l(θ)在上单调递增,所以0＜l(θ)＜12π。

综上,所求总弧长的取值范围是(0,12π]。

三、解答题

17.(1)由三视图可知,该几何体是一个平行六面体,如图1,其底面是边长为1的正方形,高为所以该几何体的体积

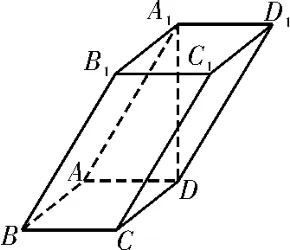
图1

(2)由三视图可知,该平行六面体中,A1D⊥平面ABCD,CD⊥平面BCC1B1,所以AA1= 2,侧面ABB1A1,CDD1C1均为矩形。所以该几何体的表面积

18.(1)连接AC,交BD于点O,连接PO。因为底面ABCD是菱形,所以AC⊥BD,BO=DO。

由PB=PD知PO⊥BD。再由PO∩AC=O知BD⊥平面APC,因此BD⊥PC。

(2)因 为E是PA的 中 点,所 以由PB=PD=AB=AD=2知△ABD≌△PBD。因为∠BAD=60°,所以又PA=所以PO2+AO2=PA2,即PO⊥AC,故

由(1)知BO⊥平面APC,因此V三棱锥P-BCE

19.建立如 图2 所示的空间直角坐标系。

图2

(1)由A1(1,0,1),得设E(1,a,0),又D1(0,0,1),则

(2)m=(0,0,1)为平面DEC的法向量,设n=(x,y,z)为平面CED1的一个法向量,则所以

由C(0,2,0),得则n即所以

20.(1)由题意可知AC⊥BC,又平面PAC⊥平面⊙O,平面PAC∩平面⊙O=AC,所以BC⊥平面PAC,所以BC⊥PA。又PA⊥PC,PC∩BC=C,PC⊂平面PBC,BC⊂平面PBC,所以PA⊥平面PBC。

(2)方法一:如图3,过P作PH⊥AC于H,由于平面PAC⊥平面⊙O,则PH⊥平面⊙O,则∠PCH为直线PC与⊙O所在平面所成角,所以∠PCH=60°。过H作HF⊥AB于F,连接PF,则PF⊥AB,故∠PFH为二面角P-AB-C的平面角。

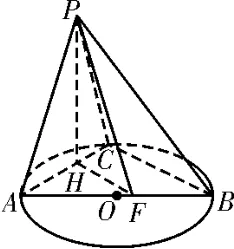
图3

由已知∠ACP= ∠ABC=60°,∠CAP= ∠CAB=30°,在Rt△APC中,PH=AP·sin 30°=AC·cos 30°·sin 30°=由AP2=AH·AC,得AH在Rt△AFH中,FH=故故即二面角P-AB-C的余弦值为

方法二:过P作PH⊥AC于H,则PH⊥平面⊙O,过H作HF∥CB交AB于F,以H为原点,HA,HF,HP分别为x轴,y轴,z轴建立空间直角坐标系,如图4 所示,则从而

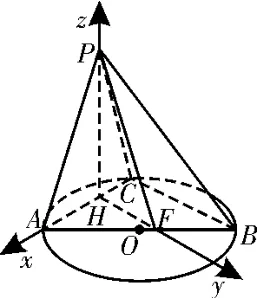
图4

设平面PAB的一个法向量为n=(x,y,z),则得令x=1,从而

而平面ABC的一个法向量为m=(0,0,1),故即二面角P-AB-C的余弦值为

21.(1)因为SA⊥平面ABCD,BD⊂平面ABCD,所 以SA⊥BD。 因 为 四 边 形ABCD是菱形,所以AC⊥BD。因为AC∩AS=A,所以BD⊥平面SAC。因为BD⊂平面EBD,所以平面EBD⊥平面SAC。

(2)设AC与BD的交点为O,以OC,OD所在直线分别为x轴,y轴,以过O垂直平面ABCD的直线为z轴建立空间直角坐标系,如图5所示,则A(-1,0,0),C(1,0,0),S(-1,0,2),B(0,-0)

图5

设E(x,0,z),则

设平面BDE的一个法向量n=(x1,y1,z1),由可求得n=(2,0,1-λ)为平面BDE的一个法向量。

同理可得,平面SAD的一个法向量为

因为平面BED与平面SAD所成的锐二面角的大小为30°,所以解得λ=1,所以E为SC的中点。