基于反步法的差动转向无人车辆轨迹跟踪*

余卓平，侯誉烨，熊 璐，陈素琴

（同济大学汽车学院，上海 201804）

前言

差动转向无人车辆（SSUV）主要应用在一些特殊场景来提高六轮车辆在崎岖道路上的转向行驶能力。而高速极限转向或湿滑工况要求作战车辆配备一个侧向稳定性控制系统，这使SSUV在军事领域受到广泛关注。

SSUV高速路径跟踪控制系统为欠驱动机械系统，并呈现高阶强非线性非仿射输入的特点。车辆质心侧偏角作为系统的内动态，不能被任意配置。如何实现高速下SSUV路径跟踪时内动态的稳定是目前存在的难点。

在SSUV路径跟踪控制器的研究中，动力学模型是路径跟踪控制器设计和分析的基础。常用模型采用车辆笛卡尔坐标和航向角来表述车辆的位置和方向。相关研究广泛采用非完整约束建模［1］，其中以零质心侧偏角假设最为常见。另外一种常在SSUV上施加的非完整约束是假设车辆运动的瞬心在车辆坐标系纵轴上投影为定值，如图1所示。通过忽略低速运动的SSUV的侧滑运动，来降低问题的复杂性。但非完整约束并不适用于高速大侧向加速度工况下的轨迹跟踪系统。另一方面，一些研究人员则不采用任何非完整约束，直接建立车辆的动力学方程。本文中面向SSUV高速运动控制系统设计，因此采用第2种建模方式。

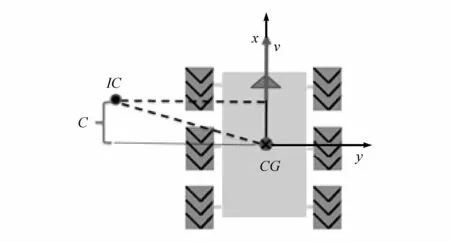
图1 瞬心纵向分量固定约束

现有的对于系统内动态镇定的非线性控制方法主要有以下几种研究方法。对于简单的系统，可采用在平衡点处局部线性化后用线性的方法设计控制。显然，局部线性化具有一定的局限性。另外，当系统具有特殊的结构形式时，可运用相对应的特定方法进行镇定。比如，对于下三角结构的系统采用反步法进行镇定。但一般来说，为维数较高的非线性系统设计具有全局稳定性质的控制器十分困难。比较常见的解决方案是将高维的系统分解为若干个维数较低而互联的子系统。

近来，SSUV控制逻辑受到越来越多的关注，Jackson等［2］采用了直接横摆力矩控制来提高六轮车辆在转向时的稳定性。Kang等［3］通过分层控制思想直接控制轮胎力来实现轨迹跟踪控制。Yi等［4］设计了一个滑模跟踪控制器并提出了相应的李雅普诺夫稳定性分析。滑模控制可实现对不同参考轨迹渐进地稳定跟踪误差［5-6］。Aslam等［7］针对高速转向的差动车辆设计了一种鲁棒的反馈控制器。而文献［8］中提出最优控制方法和非线性模型预测控制方法。Elshazly等［9］提出了一种LQR控制器并对降阶的增广动力学模型采用前馈补偿。对比这些方法，反步法比较容易实现输入状态稳定。反步法具有构造性的特点，不依赖系统参数的完全精确，也更容易实现鲁棒与自适应控制。文献［10］中通过有界反步法实现了存在执行器饱和情况下的非最小相VTOL飞行器对参考状态轨迹的输出反馈跟踪。文献［11］中则通过一步向前反步法实现了Uni-cycle的全部饱和轨迹跟踪控制。不难发现，反步法适用于差动转向车辆的控制，本文中将设计基于反步法的轨迹跟踪控制器。

1 车辆模型

选择目标轨迹上目标点的切线方向和其垂直方向构成衡量跟踪误差的坐标系，如图2所示。选择车辆状态变量为跟踪误差ex和ey，可得如下状态方程：

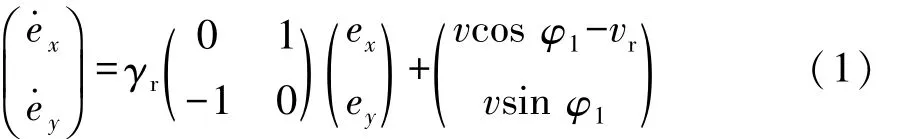
式中：φ1为实际车速v与目标车速vr的夹角；φ2为纵轴xr与大地坐标系X轴的夹角；γr为目标横摆角速度。忽略滚动阻力、空气阻力和坡度阻力后，车辆动力学状态方程为

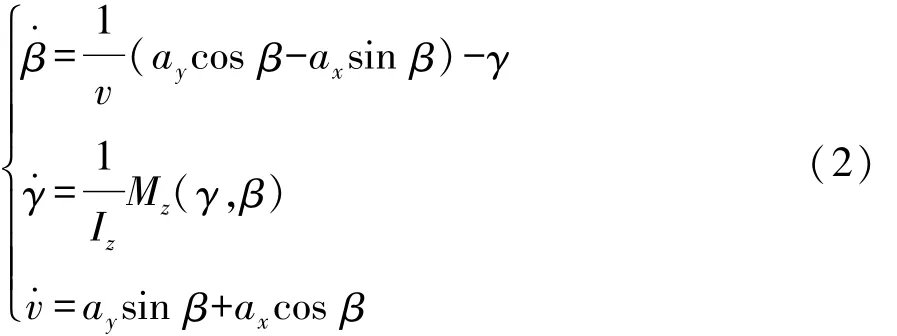
式中：β为质心侧偏角；ax和ay分别为纵向和侧向加速度；γ为横摆角速度；Iz为转动惯量；Mz为作用到车辆上的横摆力矩。

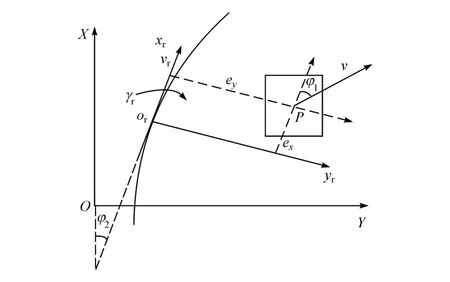
图2 车辆轨迹跟踪动力学

2 动力学控制器

对于差动转向无人车辆的控制系统，本文中采用分层控制方法来设计控制器。由于系统欠驱动和内动态不稳定的特点［12-13］，直接处理输出跟踪问题会导致系统不稳定［14］，故将系统转换为平衡点镇定问题。假设参考航向角的1阶导数和目标车速不随时间而变，即车辆动力学系统存在平衡点，而控制器的目标就是镇定该平衡点，然后通过考虑平衡点的变化作为系统的扰动从而保证控制器的鲁棒性，系统如图3所示。

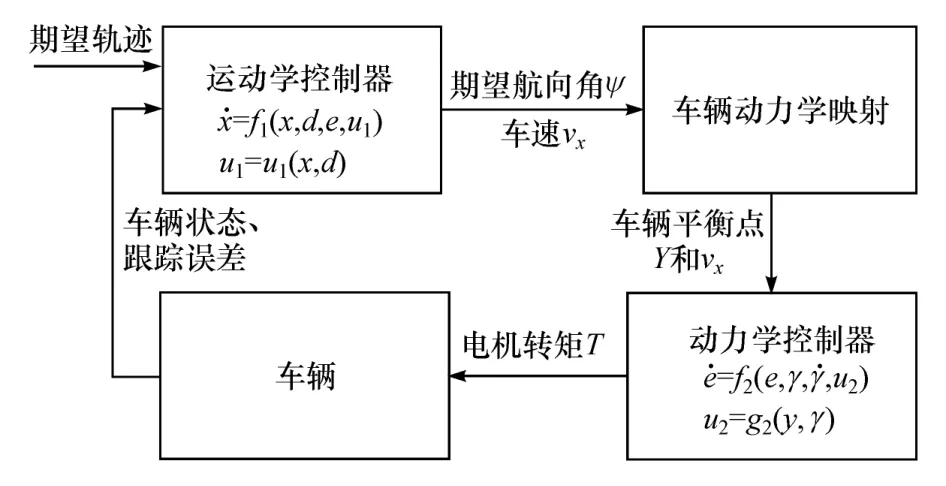
图3 差动转向无人车辆控制系统

2.1 车辆速度控制

定义跟踪误差 v～x＝vx-vxc，其微分方程为

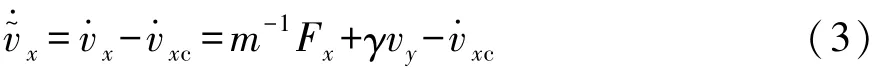
设计反馈线性化控制律以跟踪目标车速：

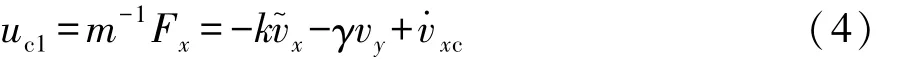
但式（4）可能产生过大的需求纵向力，同时也可能导致侧向力的严重丧失，加剧车辆失稳和侧滑。因此，当车辆速度误差超过一定限度时，施加如下饱和控制：

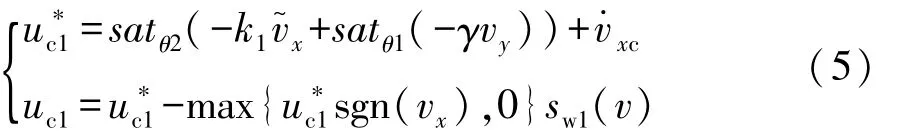
式中：k1＞0，θ2＞θ1＞0；sw1（v）为在 vthre1与 vthre2之间从0～1的一个连续过渡函数。假设参考车速一定，则车速将被保持在上边界vthre2以下。

分析车速vx＞0的情况，考虑v≥vthre2的情形。如图4所示，当且，则

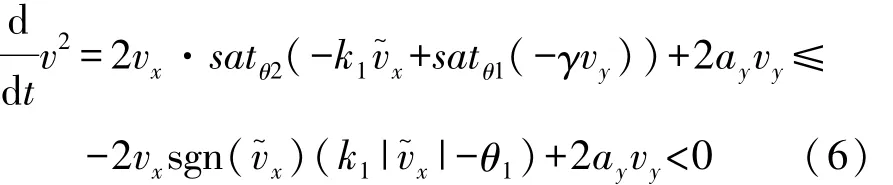
另一方面，当 ｜vx｜≤k1-1θ1＋vxc，利用 v≥vthre2＞

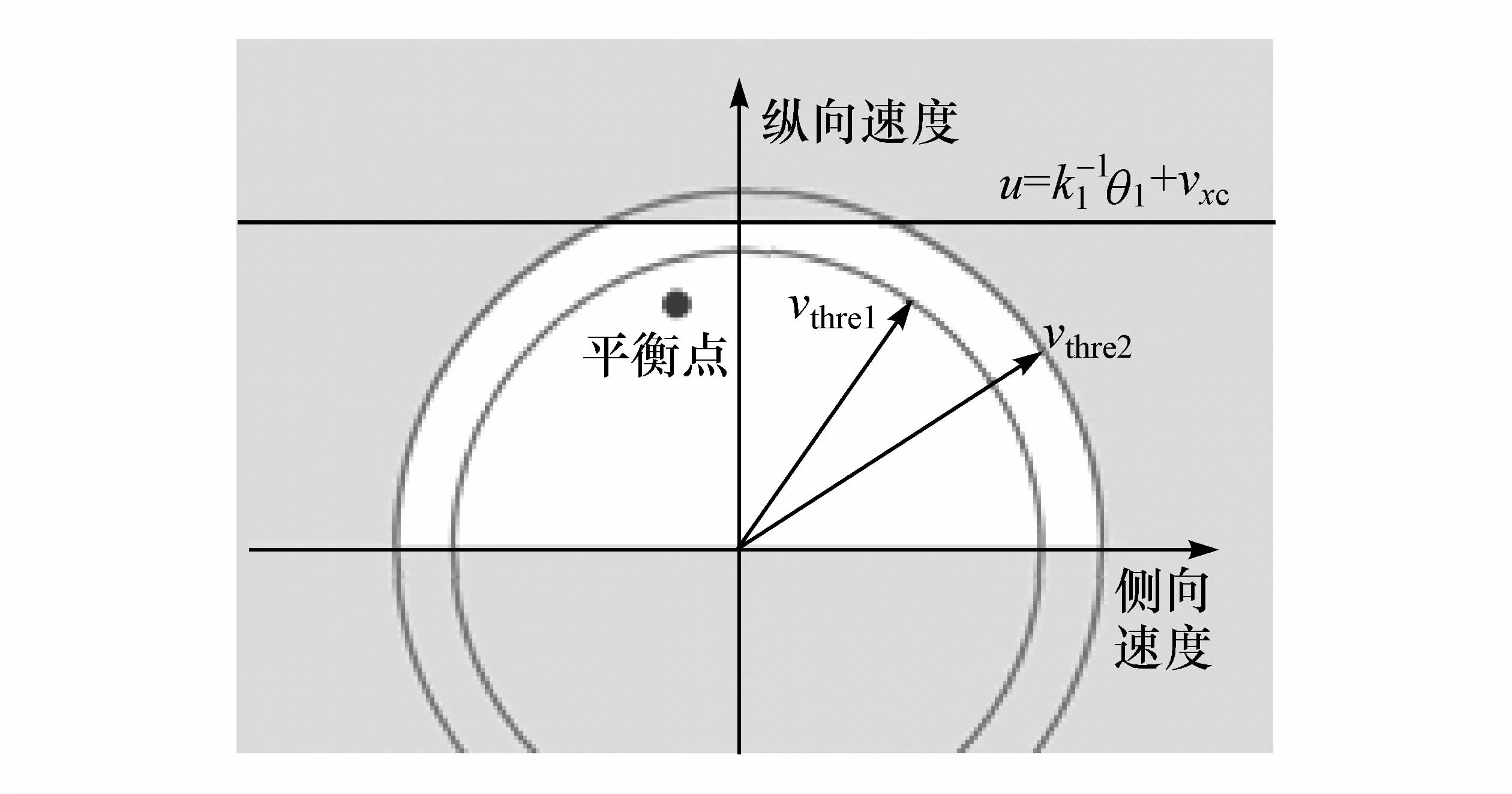
图4 速度控制域

由式（5）可知，因为 v≥vthre2所以 axvx＜0。且当车辆速度较高时，vy≠0，ayvy＜0。故v≥vthre2，v·＜0，因此车速将得到限制。

2.2 车辆横摆运动控制

定义跟踪误差 β～＝β-βs，γ～＝γ-γs，则其微分方程为

其中：

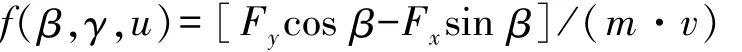
式中：βs和γs为侧偏角和横摆角速度在平衡点处的值；u为控制器的输入当运动控制层给出的航向角的2阶导数满足对应车辆的一个平衡点，则其 1阶导数满足条件0），则质心侧偏角跟踪偏差的微分方程可做以下变换：

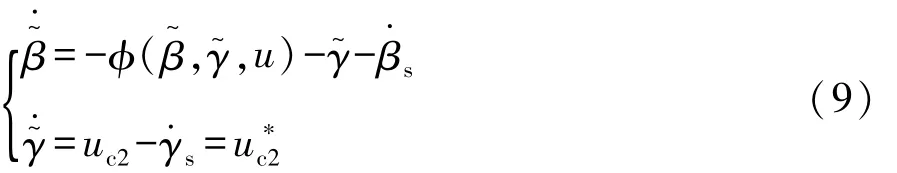
如式（9）所示，状态方程具有上三角结构特点，因此可参考反步法对其控制律进行设计。

对伪控制输入进行求导，可得

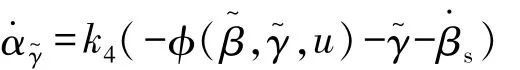
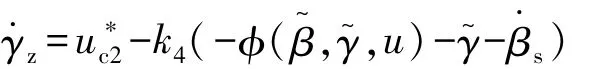
选择实际控制输入为

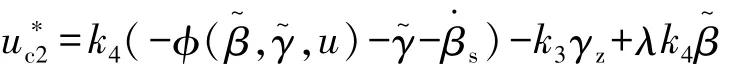
则系统的微分方程可改写为

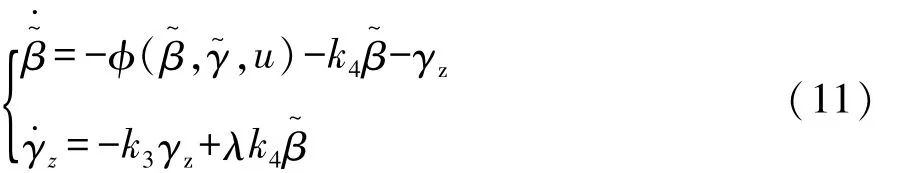
选择如下的李雅普诺夫函数：

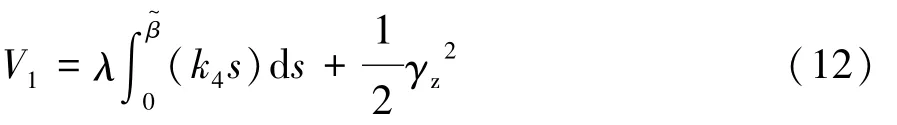
对其求导可得

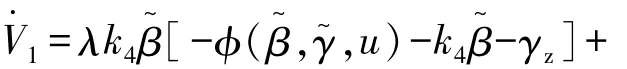
研究表明，车辆在非极限条件下，轮胎的纵向力和横摆力矩对侧向力的影响不大，故可得

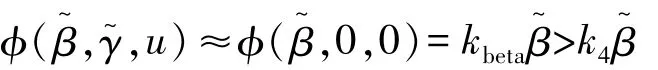
式中kbeta为车辆的等效侧偏刚度。则

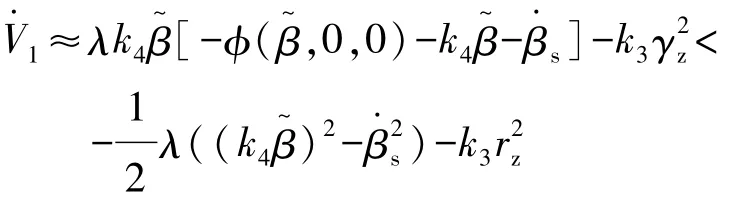
因此，通过约束上层运动控制输出的目标参考质心侧偏角的变化速率，选取合适的控制参数，λ＞0，k3＞0，k4＞0，能保证系统误差的一致有界性。控制律保证了系统是稳定的，且状态边界为为了保证鲁棒性和减少偏差［15］，本控制律进一步加入了抗饱和积分控制，具体控制律为

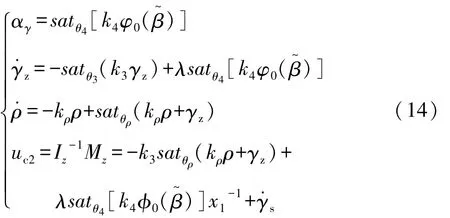
不难证明，设计的饱和控制参数满足：

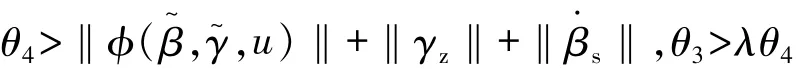
2.3 车辆航向角控制

针对航向角控制系统：

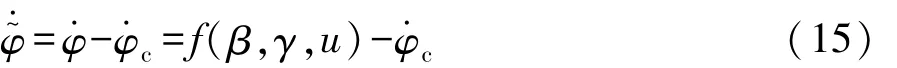
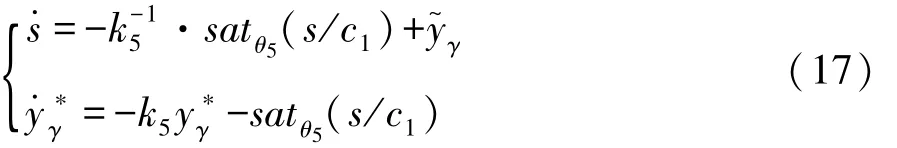
其中 k5＞该控制律保证了有 界，且 满 足 边 界 约 束另外，如果考虑李雅普诺夫函数其中 a＞0，b＞0，对其求导得

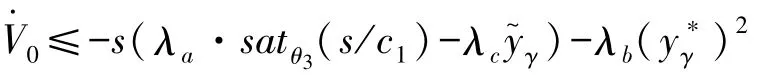
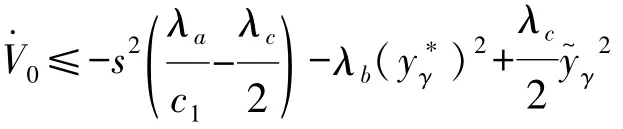
由上式可知，若参数满足条件：k5＞0，θ5＞0，c1＞，则加入控制器后的航向角系统为输入状态稳定，保证误差的一致有界性。满足：

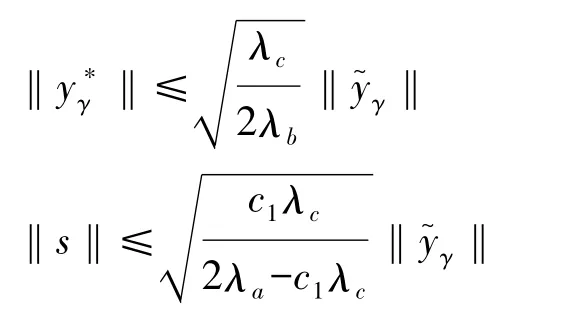
只要设计参数k5足够大，伪控制输入的跟踪误差对其影响就很弱，该系统对参考航向角的跟踪就越准确。同时新状态变量s可确保航向角误差是有界的，最终状态变量就收敛到如图5所示的平行四边形中。

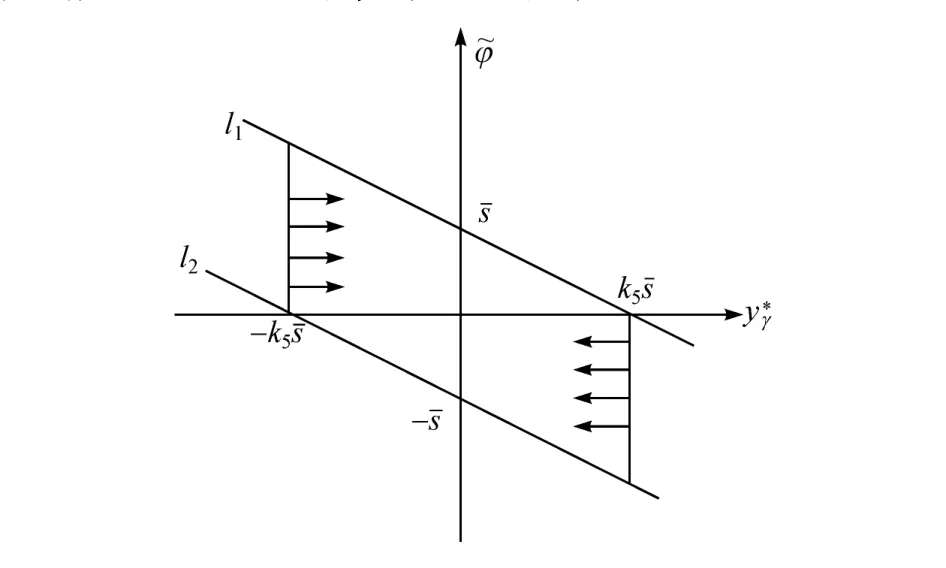
图5 航向角控制结果

3 互联稳定性分析

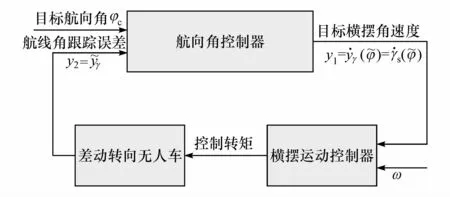
图6 互联系统稳定性分析

对于航向角子系统，可得

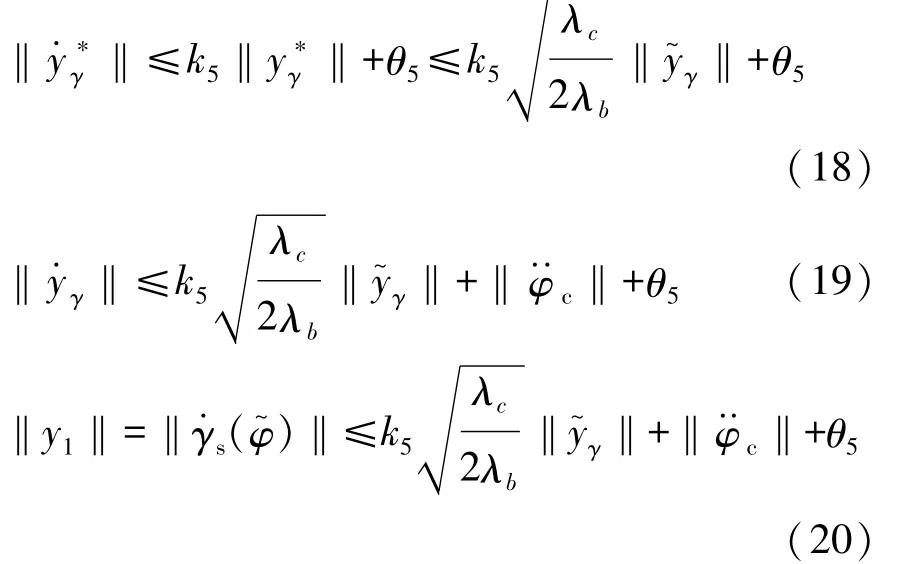
综上所述，本文中将SSUV的轨迹跟踪问题转化为对目标轨迹的平衡点镇定问题，通过变换系统误差方程，采用反步法的设计思想，对车辆的横摆运动控制和航向角跟踪控制引入虚拟控制输入，然后通过滑模控制手段和李雅普诺夫稳定性分析，保证了系统状态会收敛到运动学控制器给出的平衡点，把时变信号作为平衡点的扰动并证明控制系统的输入状态稳定。

4 仿真结果

为验证控制效果，在仿真环境中分别设置蛇行路径工况和变曲率圆周路径工况，目标航向角分别为，车辆目标速度为20 m／s，初始条件：车速为 6 m／s，跟踪误差为 0，车辆侧向速度和横摆角速度均为0。图7和图8分别为变曲率圆周路径跟踪和蛇行路径跟踪的仿真结果。由图可见，车辆能很好地跟踪给定路径，对于曲率变化的情况也能迅速响应并跟踪，满足路径跟踪需求。

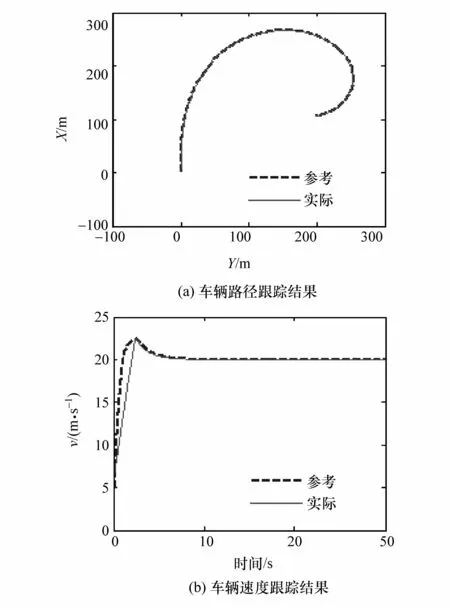
图7 变曲率路径跟踪仿真结果

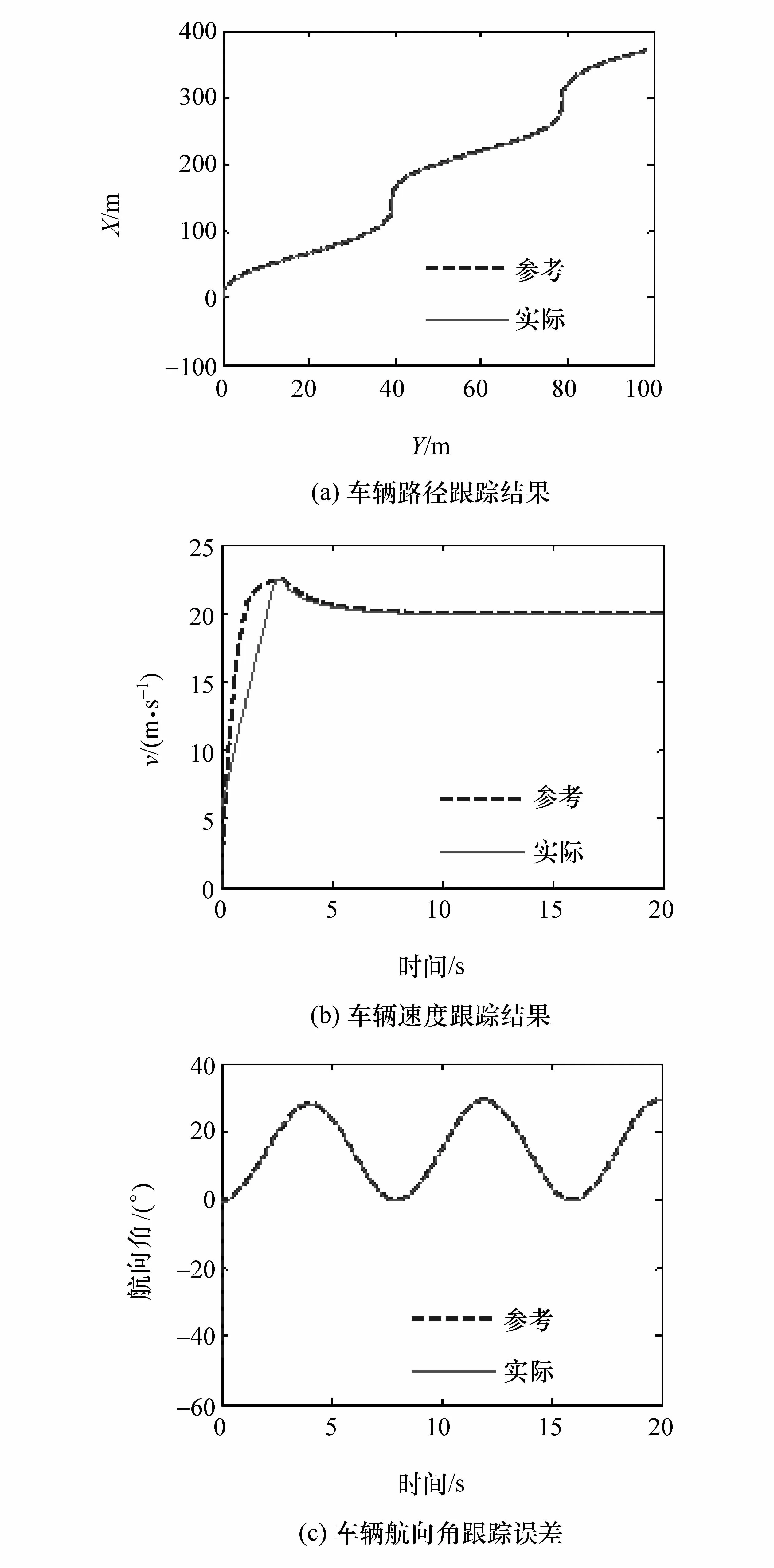
图8 蛇行路径跟踪仿真结果

当车辆初始跟踪误差较大时，为验证控制系统具有一定的鲁棒性，必须验证车辆跟踪目标路径的稳定性。设置车辆具有较大初始位置误差的变曲率圆周工况，目标车速12m／s，车辆的初始位置误差为（-5 m，5 m）。

由图9可见，运动控制系统能在较短时间内保证车辆的状态收敛至目标轨迹。

通过上述仿真工况验证，能够获得如下结论：

（1）本文中设计的轨迹跟踪控制器具备良好的跟踪性能，即使动力学控制器对于航向角的跟踪存在一定的误差，但只要误差能保持在一定的范围内，就不会影响到系统对路径的跟踪稳定性，且跟踪误差能收敛到设计的边界内；

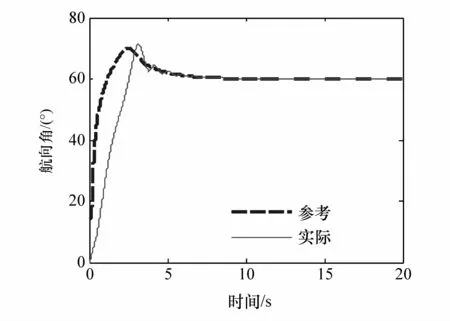
图9 较大初始误差航向角跟踪仿真结果

（2）该跟踪控制器具有较大的吸引域，即使在车辆初始状态处于较大偏差时，仍可快速稳定车辆并消除跟踪误差，使车辆跟踪目标轨迹；

（3）控制器对于直线、圆周和蛇行路径都具有良好的跟踪性能，且在低、高速或大侧偏角工况下，都能使车辆稳定跟踪目标轨迹，但随着车速增加，车辆的振荡过程和收敛时间会增加。

5 结论

针对差动转向无人车辆动力学轨迹跟踪问题，分析了差动转向车辆欠驱动系统的特点。在此基础上，将动力学轨迹跟踪问题转变为车辆瞬时平衡点镇定问题。相应地，根据反步法设计方法，设计了利用积分抗饱和控制律的车辆速度控制、航向角跟踪控制和横摆运动控制算法。动力学控制系统的互联稳定性保证了在满足航向角1阶导数为零或常数的条件下，车辆能快速、稳定地跟踪上期望轨迹。仿真结果表明，即使在高速大侧向加速度工况和初始误差较大的情况下，车辆仍然能跟踪目标轨迹，验证了算法的有效性。今后的进一步工作将是对控制系统进行实车试验，以验证控制算法的有效性。