汽车表面湍流压力脉动计算精度的研究

王 俊，陈如意，2

（1.重庆长安汽车股份有限公司汽车工程研究总院，重庆 401120； 2.汽车噪声振动和安全技术国家重点实验室，重庆 401120）

前言

汽车的气动噪声研究越来越受关注。计算流体动力学（computational fluid dynamics，CFD）技术的应用不断推动汽车的气动噪声领域的发展，而计算精度则是CFD技术的关键部分。

很多研究人员使用简化造型模型进行汽车气动噪声研究，主要是因为整车模型建模复杂，且计算容易发散。然而，造型模型未考虑气流在机舱和底盘中的流动，且受限于硬件资源，所使用的计算网格能否满足工程要求的精度，以及如何提高计算精度，这些问题均需深入研究。

文献［1］和文献［2］分别就现代和奔驰汽车运用CFD技术对汽车侧窗区域的气动噪声进行研究，分析模型和测试样车保持一致，封闭进气格栅和车底，排除了机舱和底盘的影响。文献［3］中就欧宝汽车运用CFD计算雨刮气动噪声，使用模型处理方式与上述文献相同。这些模型均为简化模型，且与国内常用的造型平底空气动力学模型有明显区别。文献［4］中对铃木汽车使用底盘平整化几何模型，与国内常用的造型模型相似，但在轮眉处用平板遮蔽了车轮，通过流向尺寸为1.5 mm的体网格计算得到压力脉动频谱，并与风洞试验对比，在1～4 kHz频段内吻合较好，但在1 000 Hz以下误差明显。文献［5］中对上汽的荣威车型进行外表面气动噪声特性研究，运用造型平底模型进行大涡模拟与试验对比，展示的两个测点中便有一个测点在700 Hz处出现了误差急剧增大的现象。文献［6］中对长安汽车运用造型平底模型进行侧风工况下的A柱气动噪声研究，对比了侧窗表面压力脉动与CFD计算结果，大部分测点在3 000 Hz出现误差急剧增大。

根据上述状况，本文中以某款轿车为对象，对如何建立几何模型进行气动噪声计算和提高计算精度做进一步研究。首先运用烟流试验初步确定整车计算模型的流态是否正确，再在此模型基础上用脱涡模拟（detected eddy simulation，DES）获得后视镜的流动状态和侧窗表面测点的声压频谱图，然后对比风洞试验结果来研究网格尺寸、几何模型对湍流压力脉动的计算结果的影响，最终确定后续气动噪声分析所需的网格尺寸和几何模型。

1 计算方案

按常规使用带机舱和底盘的全细节模型进行风洞试验，并与造型简化模型进行对比，所用的几何模型如图1所示。整车模型已经通过了风洞试验的空气动力学标定。

图1 计算所用的几何模型

设计3个计算案例，如表1所示。CFD01与CFD02用于网格尺寸对比；CFD02与CFD03用于几何模型对比。在关注的侧窗区域分别采用2 mm（Block Side Glass）和 1mm（Block Mirror）的加密区，如图2所示，考虑受限的计算资源和测点分布，1 mm的加密区是在原2 mm基础上增加了覆盖后视镜和侧窗测点的区域，并未作替换。

图2 侧窗加密区域设置对比

计算选用新的DES方法，即基于Menter K-Omega SST湍流模型求解Navier-Stokes方程的IDDES（improved delayed detected eddy simulation）方法。其思想是保持模型中的耗散率方程不变，通过改进湍动能输运方程的耗散项实现 RANS到LES的转换［7］。

分析设定入口速度为120 km／h，大气压力出口，求解域尺寸和设置与空气动力学分析一致。通过设置总厚度1 mm的7层边界层（增长率为1.2），来保证DES分析中Y＋值≤5的要求。计算在一台32核的工作站进行，生成切割体网格数和瞬态计算历时0.3 s物理现象（气流流过汽车表面）的耗时，如表1所示。

表1 计算模型对比

2 计算精度研究

在上海地面交通工具风洞中心进行气动声学测试。测试过程中，风洞边界层抽吸和移动带装置均关闭，样车的进气格栅与底盘均未封闭，与CFD的整车计算状态保持一致。

2.1 稳态计算的流态

图3为基于CFD01案例、用雷诺时均方法算得的侧窗区域分离区和风洞中的烟流测试对比。可以看出，两者均显示出气流脱离后视镜表面的剪切层呈扩张状态，使尾涡区较大，两者显示出一致的趋势，表明后视镜流线型设计效果较差。

图3 平均流场对比

2.2 湍流声压级的计算精度

以雷诺时均的计算结果为初始值，再进行瞬态DES计算，获得侧窗表面测点压力的时间历程，最后应用快速傅里叶变换获得湍流压力脉动的声压级频谱图，与风洞试验结果进行对比。测试采用B＆K公司的表面传声器和HEAD acoustics公司的采样设备，在驾驶员侧布置3个测点，测量2次，测点处于A柱和后视镜的影响区，如图4所示，图中的标记‘1-1’表示第1次测试的第1个测点，余者类推。本文中并未对侧窗上气流再附着区进行布点。使用HEAD Artemis软件进行后处理，得到各测点的声压级频谱图。

图4 测点分布图

图5 为不同网格尺寸计算与实验结果的对比。由图可见：CFD01使用2 mm网格计算所得结果在2 000 Hz范围内，绝大部分测点的计算值与测试值较吻合，但高于该频率后，计算值会急剧衰减，明显低于测试值，这与文献［1］、文献［2］和文献［5］中的情况一致，该频率被称为“截断频率”；当CFD02运用1 mm加密区后，高频出现急剧衰减的情况被明显改善，但是在3 000～4 000 Hz时，计算曲线仍然会出现拐点，低于测试曲线少许。

图5 不同网格尺寸的对比

文献［8］中提出了CFD计算的截断频率Fc的评估公式为

式中：ε为湍流耗散率，m2／s3；Δx为局部体网格尺寸，m。由此可得2 mm和1 mm体网格的截断频率分别约为1 900和3 000 Hz。显然，本文计算结果与之相符。

图6为1 mm网格不同几何模型计算结果与实验结果的对比。可以看出：侧窗运用1 mm加密区后，CFD02的整车模型与CFD03的造型模型在中频和高频的计算结果基本无差别，只在100 Hz以内的低频存在一些差别。推测该低频的差别，源于气流流经车体上下表面的流量比例和到达侧窗区域的气流速度的差异。

表2为各测点的总声压级。由表可见：CFD01的总声压级误差范围为2.0～6.3 dB；而CFD02的总声压级误差范围为0.1～5.4 dB，改善明显。对比CFD03总声压级误差范围为0.4～6.2 dB，可以看出在精细网格上应用整车几何模型后，CFD02的误差稍小，但优势不如细化网格明显，出现较大误差的3个测点的误差仍然较大。

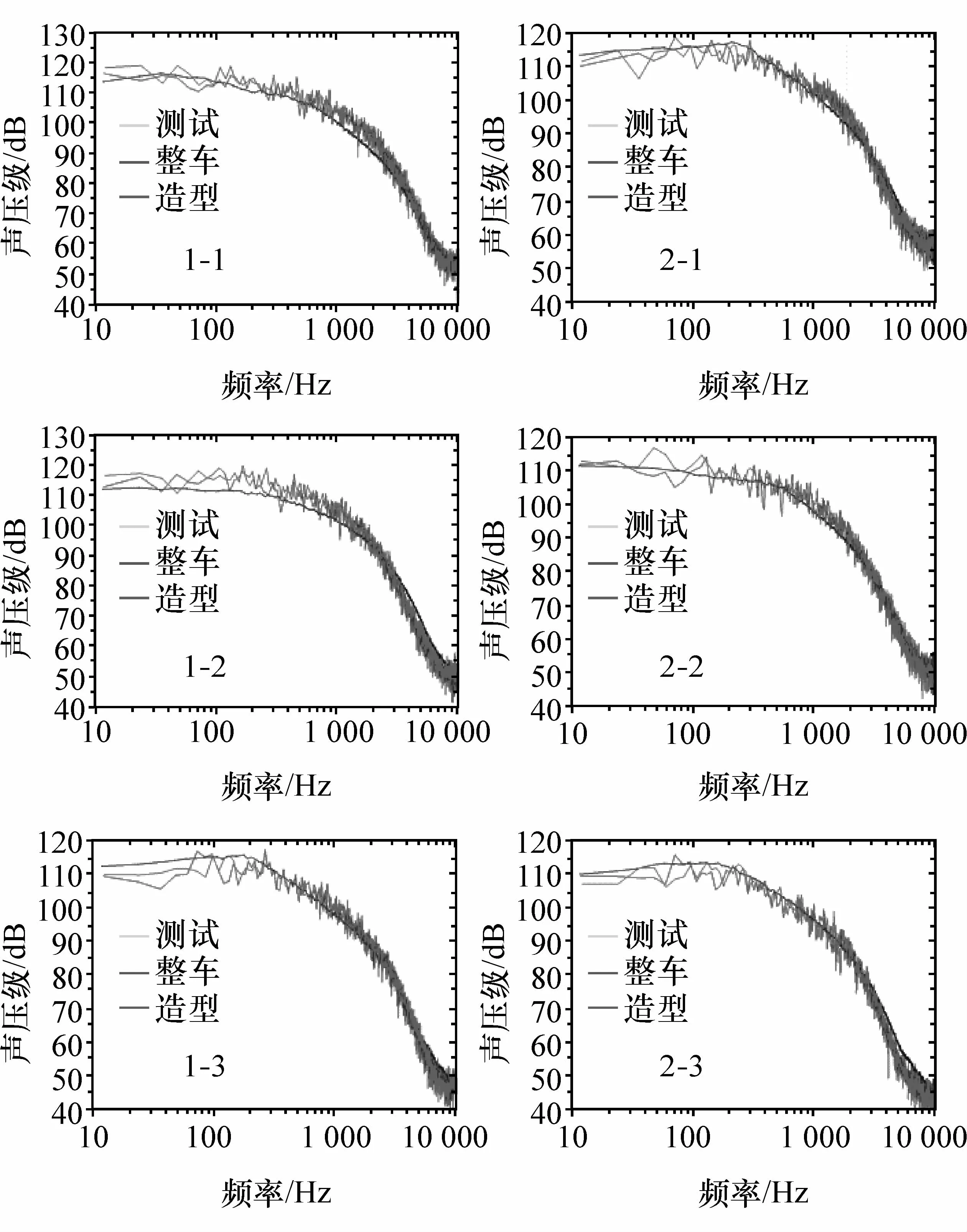
图6 1 mm网格不同几何模型的对比

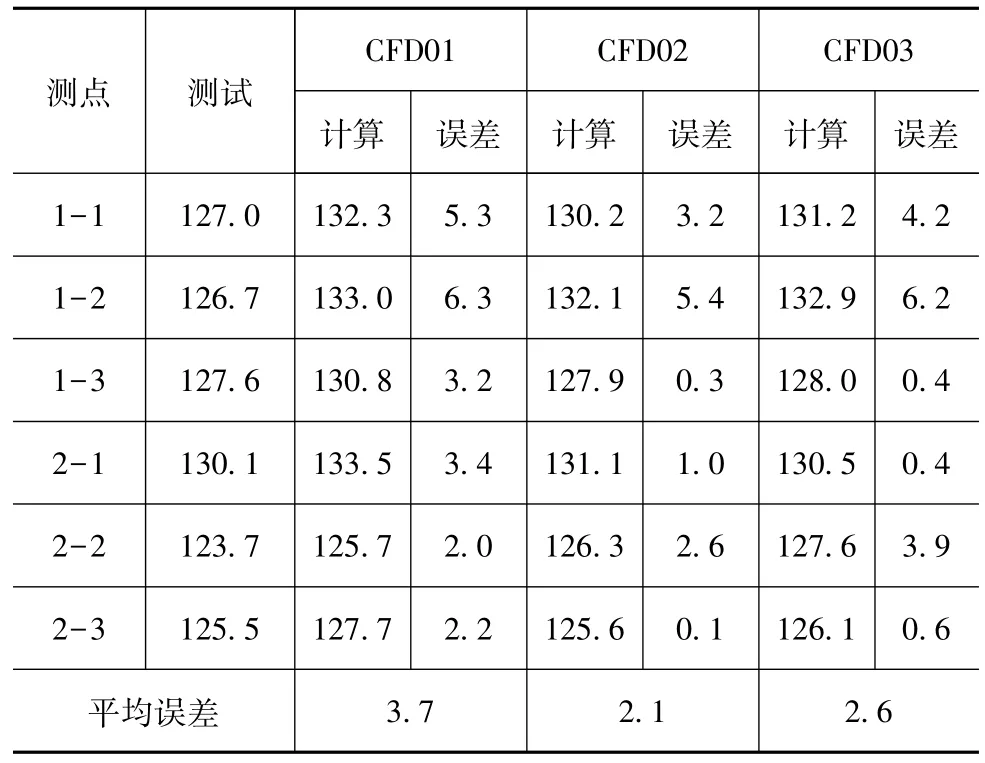
表2 总声压级对比 dB

3 计算结果分析

3.1 Q准则对比

通过定义一个正值的Q准则［9］等值面来显示涡核，并用涡量着色，获得如图7所示的非定常流场的流态。可以看出，气流流过A柱而形成沿A柱方向的纵向涡流，后视镜尾部形成了环状涡流结构。后视镜的涡量值和涡流覆盖的区域均大于A柱，据此推测该后视镜会是一个明显的噪声源。

图7 非定常流的流态显示

根据涡声理论，在流速很低的条件下，仅仅存在涡的地方才会产生声音［10］，且涡是流动的声音［11］。因此，准确捕捉涡核便能更好地定量噪声源。通过对比可得，在后视镜附近区域，与 CFD02相比，CFD01的涡核尺寸较小，涡量较大，很明显1 mm网格尺寸能捕捉到这些尺寸较小的涡，因此，在频谱上高频段的误差明显改善。

3.2 湍流压力脉动的对比

侧窗区域噪声源之一的偶极子噪声对应于面声源。可用压力脉动的标准差来评估偶极子声源，其定义为

式中：p为某时刻下的瞬态压力；p-为平均压力。pRMS是统计意义上的物理量，其数值越大，表明该位置的流场随时间变化越剧烈，流场扰动引起的声载荷越强［12］。用压力系数将压力进行无量纲化，获得无量纲化的压力脉动。

图8为车身表面的压力脉动分布的对比。可以看出：3个方案的总体分布类似，后视镜基座附近的压力脉动非常明显，达到0.3；在侧窗玻璃上，临近A柱区域的压力脉动达到0.2，也较为明显，从而形成了后视镜和A柱的气动噪声影响区。从三者的侧窗分布来看，CFD02和CFD03的结果较为接近。因此考虑到计算效率，建议湍流压力脉动的计算采用造型模型，且使用1 mm的加密区。

图8 表面压力脉动分布对比

4 结论

通过DES方法计算汽车侧窗区域的流场，并与风洞试验对比，获得如下结论。

（1）使用1 mm网格比2 mm网格可获得精度更高的湍流压力脉动计算结果，特别是在值得关注的2 000 Hz以后的高频段，误差会明显减小，便于后续声场的精确分析。

（2）从Q准则来看，1mm加密区能捕捉较小的分离涡，因此，其在高频上的精度会更高。

（3）造型模型可快速建模，提高计算速度和稳定性，在气动噪声所关注的中高频段与整车模型的结果一致，整体不明显降低计算精度。鉴于湍流压力脉动的计算结果对网格的细密度十分敏感，建议优先选用造型模型且使用1 mm的加密区。