无刷直流电机直接转矩控制系统的优化设计

张雷 李航 宋晓娜

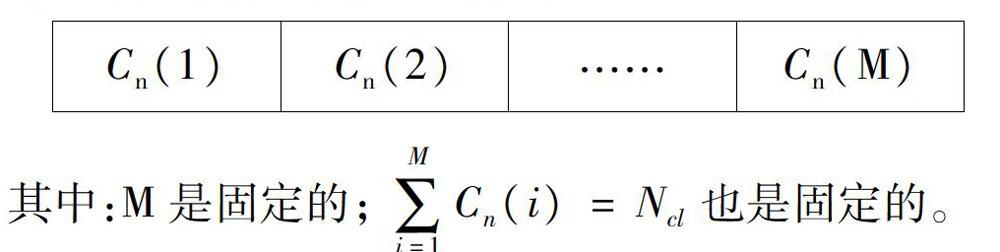
摘要：为了获得较为精简的模糊控制规则集合和改善控制性能，提出了一种基于进化多目标优化算法的模糊控制器优化设计方法，并应用于无刷直流电机直接转矩控制系统。该控制系统采用模糊控制器作为转速环的调节器，內环则为转矩控制环，并且采用了无磁链滞环的控制结构。同时提出了一种改进的多目标克隆选择算法，可针对模糊控制器的结构和参数进行优化，并选取典型的控制性能指标，以及模糊控制器自身的精简度作为优化目标。为了提高算法的搜索效率和利用偏好信息，有针对性地提出了种群多样性保持策略和偏好策略。实验结果表明这种优化设计方法可获得良好的动态响应性能和较强的自适应性，同时所得到的Pareto优化解具有较好的分布特性。

关键词：无刷直流电机;直接转矩控制;模糊逻辑控制器;多目标优化;进化多目标优化算法

DOI：10.15938/j.emc.2019.10.013

中图分类号：TM 33文献标志码：A 文章编号：1007-449X（2019）10-0110-10

0引言

无刷直流电动机（BLDCM，brushless DC motors）由于具有高效、低成本、体积小等优势，因而目前在小功率的家用电器领域得到了广泛的应用。实际上，无刷直流电机还具有结构简单、高磁通密度、高功率密度、可靠性高和维护方便等众多优点，既保留了传统有刷直流电机良好的动态性能，但是没有机械式换向器和电刷，因而还拓展到工业控制工具、机器人、精密伺服系统、医疗设备、航天等应用领域。

无刷直流电机转速调节过程中的动态性能和稳态误差，对于高性能的无刷直流电机驱动系统尤其重要，特别是在针对系统速度和位置的控制。无刷直流电机在应用中存在一个突出的问题即转矩的脉动问题，这会带来电机的振动和噪声，还会降低系统的运行性能，因此转矩脉动抑制和改善也是该领域研究人员所关注的一个重要研究方向。

直接转矩控制技术的应用就是其中的一种抑制方法，其思想是直接控制电机的瞬时转矩，并且将转矩的脉动视为是一种可测干扰，这可通过构造转矩闭环控制结构来实现。直接转矩控制技术最早是针对异步电机的交流调速系统所提出的，现已被广泛应用在多种类型电机的控制系统中。这种技术从本质上讲是对电磁转矩的直接控制，而不是通过控制电机的电枢电流来间接控制转矩。

目前许多研究成果应用直接转矩控制技术来设计无刷直流电机驱动系统，获得了较好的控制效果。由于传统的异步电机和永磁同步电机的气隙磁场均为正弦波，而无刷直流电机的气隙磁场波形则近似为梯形波，并且其电枢电流理想波形为矩形波，因而在设计无刷直流电机的直接转矩控制系统时需要考虑这些特点，并进行相应调整，比如磁链的计算、扇区的划分方式以及电压矢量选择表等。总的来讲直接转矩控制技术优势在于控制结构简单，具有较好的动态性能，并且电机参数的变化对系统性能的影响较小。但是其不足主要体现在：磁链给定值和滞环调节器的宽度不好确定、逆变器的开关频率不固定、换相转矩脉动仍然较大以及系统低速性能不理想等。

针对直接转矩控制技术的改进可以结合模糊控制、人工神经网络等智能控制方法。其中模糊控制技术是一种基于模糊集合和模糊推理理论的智能控制策略。模糊控制方法无需被控对象和系统严格的数学模型，其主要是根据专家的知识和经验来构建模糊规则库，并且这种控制方法还具有较强的自适应性和鲁棒性，当前已被广泛地应用于多个领域中的控制系统设计，其中也包括无刷直流电机控制系统。

当前在电机模糊控制系统的设计方法中，模糊规则的确定大多数是依靠专家的经验和知识，这往往存在较大的主观性。如果无法得到专家经验，虽然也可以通過实验的方式进行确定，但这往往是比较困难的。不少研究人员进而尝试利用进化计算来确定模糊控制器的参数，这实质上是将模糊控制器的设计问题转化为优化问题。这种设计方案涉及到优化目标函数的构造问题，其中不同的控制性能对应于不同的权值系数，确定合适的系数也不是一项简单任务。

本文提出了一种基于多目标克隆选择算法的模糊控制器的优化设计方法，并应用于无刷直流电机直接转矩控制系统。其设计思想是采用优化后的模糊控制器取代原先转速环中的PID调节器，并且采用无磁链滞环的直接转矩控制结构。实验结果表明所得到的无刷直流电机控制系统具有较强的自适应性和良好的控制性能。同时由于是利用优化算法来确定和优化控制器的参数，因而可应用于那些无法借鉴和获取专家经验的场合。

1无刷直流电机直接转矩模糊控制系统

1.1无刷直流电机的数学模型

无刷直流电机常采用两相导通星形连接方式，为了简化计算和便于分析，常采用如下的假定条件：

1）转子的磁阻大小不随旋转位置的变化而改变，并满足三相定子绕组完全对称;

2）电枢的绕组是均匀连续分布的;

3）磁路无饱和，且忽略磁滞损耗及涡流损耗。

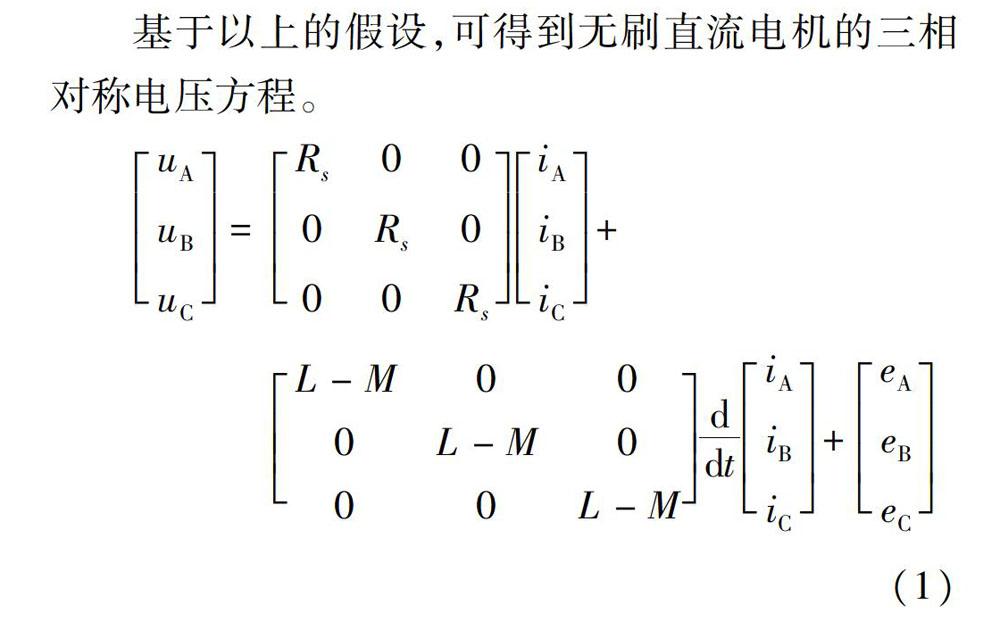
基于以上的假设，可得到无刷直流电机的三相对称电压方程。式中：u_A，u_B，u_C为电机的三相定子绕组的相电压值;i_A，i_B，i_C为定子绕组的3个相电流值;L和M则分别为定子绕组的自感和互感值;e_A，e_B，e_C为三相定子绕组中的反电动势。

1.2无刷直流电机直接转矩控制系统

控制系统采用双闭环控制结构，其中外环为转速控制环，并且采用模糊控制器作为其转速控制器;而内环则为转矩控制环，并仍然采用传统的滞环调节器作为内环控制器。图1为控制系统的结构图。

无刷直流电机直接转矩控制系统的组成单元主要包括电压型逆变器及驱动单元、开关管状态查询表、位置检测和转速估算单元、电磁转矩估算单元、自适应模糊控制器和转矩滞环调节器等。除了无刷直流电机的驱动电路外，电机转速和转矩的估算、双闭环控制的控制功能都是在采用软件的方式在DSP芯片中实现。

当隶属度函数部分编码确定之后，实际上模糊规则库中的规则数目就可以确定。对于2输入单输出系统，模糊规则库包含5×5=25条规则，其中数字“5”表示所有模糊变量均采用5个语言术语。需要调整的是每个规则的输出变量，本文设计了模糊规则库的动态调整机制，即规则库中所包含规则可进行动态调整，因为模糊规则的数目也是一个优化选项。模糊规则的编码及调整机制如图3所示。

从图3可以看出，模糊规则库中的规则数目并不固定，有些规则可从中删除。

2.3进化操作

多目标克隆选择算法隶属于一种多目标进化算法，原先也是用于解决单目标优化问题。该算法主要借鉴了生物免疫系统中的克隆选择原理，在处理复杂多模态函数优化、模式分类问题上呈现出较好的收敛能力和搜索效率。

本文利用多目标克隆选择算法来搜索和优化模糊控制器的参数。为了提高搜索的针对性和效率，对原有算法进行了改进，设置了个体多样性保持机制、个体评价和进化操作过程中的偏好策略以及算法的重启操作。

1）重启操作

在算法的迭代优化过程中，有时会不可避免地出现未成熟收敛现象或者种群中个体过于相似。当进化过程中出现连续几代未产生新的非支配解，则实施重启操作：取出记忆种群中一定比例的满足差异性条件的个体作为新的初始种群的一部分，其余部分则针对那些满足偏好条件的个体变异后获得。这样既体现了对于偏好信息的利用，也有助于避免未成熟收敛现象。

2）进化操作

与遗传算法等常用进化算法中的交叉和变异操作有所不同，本文算法所实施的进化操作包括克隆选择和变异操作，并且主要是利用个体的变异操作来产生新的个体，没有基因交叉操作。

为了避免种群中个体过于相似，克隆操作的候选个体之间必须满足一定的相似性要求。个体之间相似性涉及到种群中个体的多样性，可采用常用的距离概念进行度量。由于个体是采用实数编码，这里考虑到gray码的特点，可将编码中每位基因转化为同样长度的gray码（文中采用4位），再通过计算个体之间的汉明距离（hamming distance）来度量其相似性。同时需要设定一个阈值（D_th），与某个个体的距离小于该阈值的个体（视为相似的个体）的数目定义为拥挤度，只有当该个体的拥挤度小于另一个阈值（D_yj，拥挤度阈值）时才能進行克隆操作。该阈值是可以进行动态调整的，初始值可以取得大些，随着算法迭代可逐步减小。

随后，在确定每个进行克隆操作的个体的克隆数目时，对于那些满足决策者偏好条件的更好的个体给予更多的数目。例如，对于优化目标向量中的第i个分量，可基于决策者的偏好信息定义一个偏好函数η_i（x）（文中采用排序函数的形式），然后将所有分量对应的偏好函数的函数值进行求和，就可确定该个体满足偏好条件的偏好程度J_gp（θ_i），具体计算如公式（5）所示。式中：J_ob（θ_i）表示个体i对应的目标向量;而J_ob（θ_i）j表示其第j个分量;η_i（x）为所定义的偏好函数;m表示优化目标的数目。

接下来，将所有个体依据其目标向量并且按照偏好程度进行排序，数值越高则排序越靠前。这样在确定克隆数目时，虽然种群总的克隆数目N_cl是事先定好的，但是排序在前的个体可获得更多的克隆机会。

在实施变异操作时，首先随机确定变异的位置，然后基于变异概率P_m进行随机的加减1操作。由于个体编码中隶属度部分和规则部分的关系，可分别对这2个部分独立进行变异操作。对于隶属度函数部分，如果变异后值超出设定的范围或者违背3个参数之间的大小关系，则在相反方向重新进行变异;而对于模糊规则部分的编码，只需要满足设定的范围[0，5]即可。

对于同一个个体克隆产生新个体，它们的变异操作要对应于编码串中的不同区域，确保新个体的多样性。另外由于算法无交叉操作，在每一次的迭代过程中随机挑选若干个体，并从已得到的非支配解（保存在记忆种群）中提取部分基因加入到这些个体中，作为一种特殊和辅助的变异方式。

3）多样性保持机制

上述的克隆和变异操作，实际上在确定克隆的候选个体、克隆数目以及限定变异区域都体现了多样性保持机制，同时也体现了对于那些满足决策者偏好条件的Parcto区域搜索的针对性。另外该机制机制还体现在种群的更新过程中，那些满足决策者偏好条件的个体有更大概率进入到下一代，或者被保存下来。

所提出的改进多目标克隆选择算法的具体实施步骤如下所示。

1）确定算法的相关运行参数，包括种群规模N、最大评价次数E_max、个体编码参数M_n、克隆操作的参数C_n、D_th和D_yj，变异概率P_m;随机产生初始种群A_o和初始记忆种群M_o，并且种群和记忆种群的规模在迭代过程中保持不变，分别为S_a和S_m。

2）评价当前种群A_t（t为迭代代数）中每个个体θ_i，并针对2.1节所给出的优化目标，得到种群中所有个体所对应的目标函数向量J_ob（θ_i），表示为J_ob（θ_i）=[ISE，E_ss，T_s，R_n]。然后选取所有的非支配解作为进行克隆选择操作的候选种群。

3）克隆选择操作。克隆选择实际上包括选择操作和克隆增殖操作，即从种群中选择部分优秀个体进行克隆增殖操作，产生一定数目的新个体，它们与原个体在编码上完全相同，类似于生物学意义上的克隆操作。

候选克隆个体的数目M是固定的，并且总的克隆数目N_cl也是固定的。首先根据式（3）计算当前种群中個体的偏好程度，之后进行升序排列，并且从中移除不满足拥挤度条件的个体，然后针对剩余个体中最前面的M个优秀个体进行克隆操作。按照下面表格中的相应位置来确定克隆数目，表格前面的元素对应的值较大，越靠后越小，并且表中元素的总和是固定值。该表格可事先确定好，在运行时通过查表来确定具体克隆数目。

4）个体变异操作。每个克隆新产生的个体还会实施一个变异操作，其某些编码会随机发生改变。如前所述，变异操作体现出较强的针对性：对于相同个体克隆产生的不同新个体，变异要确保差异;另一方面对于隶属度部分和规则部分的变异是分别独立进行的，如图2和图3所示;还有就是利用提取优良基因来实施的特殊变异方式。

5）记忆种群的更新。记忆种群用于保存当前搜索得到的非支配解，随着算法的运行不断有新的非支配解加入，并且移除那些被新加入个体所支配的优化解。

记忆种群的规模设置了一个最大值S_m，当其规模超过该值后，每次新加入一个非支配解，如果此时没有出现移除被新加入个体所支配的解，则基于前面所述的拥挤度概念移除一个拥挤度值最高的解（如果多于1个，则随机选取1个）。

如果在进行记忆种群更新时，连续10代未出现新的非支配解，则实施重启操作，转到步骤3）。

6）产生下一代抗体种群。基于新生成的个体并从中选取一定数目的非支配解作为下一代抗体种群中的一部分，其余个体则用随机生成的个体进行替代。同时更新算法中新个体的评价次数。

7）算法终结条件判断。根据个体的评价次数是否达到设定最大值E_max作为算法终结条件。

当优化算法迭代结束后，可得到一个近似的Pareto前沿（pareto front），使得在系统控制性能最优化，同时也考虑到模糊规则库的精简程度。每一个优化解就对应于一个具体模糊控制器，至少在某个性能指标上是占据更大的优势的，也表示了一种折中方案可供设计人员进行选择。

3实验结果与分析

实验系统中的无刷直流电机的具体的参数如表2所示。电机控制器芯片采用TT公司的TMS320F28335，该芯片具有较多的集成资源，可方便进行电机控制系统的设计。驱动电路则采用了IR2135，利用该芯片可方便地驱动IGBT。实验结果通过串口总线可方便地将数据采集到PC机中，并进行相关的处理和比较。

无刷直流电机转速控制系统的一项主要功能就是能够实现电机转速的调节，以满足电机拖动系统在运行过程中不同状况下的工作要求。首先测试系统在额定负载的条件下，转速调节过程中的动态响应性能和稳态误差。

假定电机拖动系统在额定负载的条件下起动，初始设定转速为1500r/min，运行过程中将电机的转速减到1300r/min，待再次稳定运行后重新将转速增到1500r/min，电机的转速响应曲线以及相电流和反电动势的波形如图4所示。

从图4中的响应曲线可以看出，系统在初始的起动过程中，以及在调节转速时，过渡过程都比较短，并且可实现无超调现象，同时稳态误差基本上可以忽略。这表明所设计的模糊控制器可获得较好的控制性能，并且在不同的工况下具有较强的自适应性，动态调整控制器的相关参数。

为了定量测试和比较优化所得到模糊控制器的性能，选择了2种相似的模糊控制器设计方案作为比较对象。一种方案同样是利用本文的优化算法来确定模糊控制器的参数，但仅针对模糊规则库进行优化，而隶属度函数是采用均匀划分的三角形函数形式，用SOAF进行表示;另外一种则是文献[15]中所提出的自适应切换模糊控制器设计方案，表示为FALC，该方案能够根据不同的控制状况在模糊PI和模糊PD这2种控制策略之间进行切换，从本质上仍属于自适应模糊PID控制器。这2种方法与本文的设计方法仅在控制器的设计和优化过程中某些策略上有所不同。

不同方案进行比较的性能也就是优化目标向量中各个分量，包括模糊控制器的规则数目、绝对误差积分准则（IAE）、稳态误差和调节时间。其中规则数目用于反映模糊控制器的精简程度，稳态误差用于反映系统的稳态性能，而IAE和调节时间可反映系统动态响应性能。具体的性能比较结果如表3所示，其中的数据均为3种方法按照优化解中的IAE指标最优进行选取。

由表3中对比结果可以看出，无论是在调节时间、稳态误差还是在绝对误差积分准则等性能指标上，本文方法都可以获得最优值，这反映了模糊控制器的可调整参数优化的效果，并且在所示的工况下，模糊规则可以进行适当地删减，能够在较少的规则数目下仍然可以获得较好的性能。

对于负载突变的状况，假定系统已经达到稳定状态后，随后系统的负载发生突变，测试控制系统对应的动态和稳态性能。假定系统由加载额定负载开始起动，并达到所设定的稳态转速1500r/min，随后突然增加和减少负载，测试系统的动态响应性能以及稳态误差。负载的突变情形设置为：当系统起动并稳定运行后，首先使系统的负载突变到0.6Nm，待拖动系统重新达到新的稳定运行状态后，然后再回到额定负载。在整个过程中转速的设定值保持不变，控制系统的转速、电流和转矩的响应曲线如图5所示。

从图5中动态响应曲线可以看出，系统在负载发生突变的过程中，同样可在较短的时间内完成过渡过程，电机的电磁转矩（电流）可在较短时间内跟随负载转矩的变化，电机的转速会相应产生一个小的跳变，但是其稳态误差也基本上可以忽略。这表明优化所得到的模糊控制器在负载发生突变时具有较强的自适应性和良好的动态响应性能。

不同方法之间的性能比较结果如表4所示，同样其中数据也是按照优化方法所得到的优化解中的IAE指标最优进行选取。

可以看出，无论是在调节时间、稳态误差还是在IAE指标等性能指标上，本文MOCS方法都优于其他2种方法，并且模糊规则的数目仍然是最少的。

为了测试优化所得到的控制器对应直接转矩控制系统的抑制转矩脉动的效果，选取了传统的直接转矩控制技术作为对比方案，其控制结构中包含转矩和磁链滞环。仍然针对上述负载突变的工况进行实验，而其他的实验参数保持不变。这2种方案所得到转矩和电流波动曲线分别如图6和图7所示。可以看出，传统直接转矩控制方案的转矩脉动的幅度超过了20%，而本文方案则在12%左右，体现出较好的转矩脉动抑制效果。

最后为了测试本文多目标优化算法的搜索能力，以及优化解的分布情况，与典型的多目标优化算法进行了相应比较。为了较为直观地观察和对比，所选取的Pareto平面的横轴和纵轴分别表示模糊规则的数目和IAE性能指标。每种算法各自选择4个代表性的优化解，它们分别为横轴和纵轴2个坐标对应性能指标所获得的最优和次最优解，具体的分布情况如图8所示。

从图8可以看出，所提出的改进型优化算法可得到较为分散的Pareto优化解，在获得较好折衷解的基础上，体现了算法中个体多样性保持机制的有效性。另外，这些优化解是在个体的评价次数受到严格控制的条件下获得的，这一定程度上反映出算法较好的搜索能力和搜索效率。

4结论

本文提出了一种基于改进的多目标克隆选择算法的模糊控制器的优化设计方法，并应用于无刷直流电机的直接转矩控制系统。这种直接转矩控制策略不包含磁链滞环，而是将电机转矩直接作为被控量，因而动态响应速度更快。实验结果表明优化得到的控制器具有较强的自适应性和抗干扰能力，以及良好的控制性能。同时由于是利用进化算法来确定和优化控制器的相关参数，因而可应用到那些无法获取专家经验的模糊控制器设计场合。