具有径向通风结构的5兆瓦双馈风力发电机内流热特性
丁树业 仵程程


摘要:为了揭示具有径向通风结构电机內流体流变特性及传热规律,以一台5MW双馈风力发电机为例,依据流体力学和数值传热学基本理论,结合电机通风结构特征及冷却方式,在建立三维流热数学模型的基础上,通过给定基本假设,确定了流体流动与传热特性研究的物理模型。采用有限体积法对具有密闭循环冷却系统的径向通风电机流体场和温度场进行了数值求解,并对数值计算结果进行了详细的数值分析。阐述了电机內流体参数在轴向及径向的空间分布特性,并以此为基础研究了电机內部的温升分布特性,揭示了具有径向通风结构电机內部流体流动及热性能的耦合规律。
关键词:有限体积法;双馈风力发电机;流体场;温度场;计算流体力学
DOI:10.15938/j.emc.2019.10.008
中图分类号:TM 315文献标志码:A 文章编号:1007-449X(2019)10-0068-09
0引言
我国的能源产业发展迅速,电机在电力行业中发挥着不可替代的作用,电机的发展水平直接关系到国民经济的发展速度。径向通风电机由于其独特的结构特点被普遍应用在电力生产过程中。由于该类型电机的通风结构及原理较为复杂,因此,对具有径向通风结构的电机进行流体场及温度场的精确计算具有重要意义。对流体场和温度场的准确可靠的研究,有利于提高该类型电机多物理场的计算精度,改善径向通风电机的通风效果,进而提高电机运行的安全性、可靠性及稳定性。由此可见,对径向通风电机内流型演化及传热规律的研究显得格外重要。
目前,對于径向通风电机多物理场计算研究较少,影响其发展的因素主要有下面两方面,由于定转子径向通风槽钢的存在,当电机运行时,转子槽钢可作为离心式风扇的扇叶,不仅增加了电机机械结构复杂度,而且使电机内部多种物理场相互关系更加错综复杂,因此,对于径向通风电机流体场及温度场的研究需要解决这两方面的问题。近年来,国内外的诸多专家学者对电机结构以及电机内的流体场、温度场以及流-热耦合场进行了卓有成效的研究,为本文对径向电机的研究提供了理论指导。在对通风冷却结构的研究中,国内学者袁益超教授做了深入的研究工作,并以电机的轴向及径向通风道结构为重点对其理论及仿真方法进行了深入剖析和解读。
本文建立了三维流热数学模型和物理模型,采用有限体积法对一台具有径向通风结构的5MW双馈风力发电机的流体场和温度场进行数值研究。在明确了流量及流速等参数在电机轴向及径向空气域内空间分布特性的基础上,进一步研究了电机内部的温升特性。为具有径向通风结构电机的通风结构优化设计及热性能分析提供了理论依据。
1求解域物理模型及数学模型
1.1数学模型
电机内流体流动受到物理守恒定律的约束。当流体流动状态为不可压缩且处于稳定流动状态时,在直角坐标系中流体流动质量、动量以及能量守恒方程可分别表示为:
1.2基本假设
为了简化求解过程,作如下假设:
1)由于仅研究电机处于稳定运行状态时的流体流动情况,为定常流动,因而不考虑时间项;
2)电机内流体流动为紊流流动,计算时采用标准k-ε模型;
3)计算域内流体流速小于声速,因而不考虑空气的压缩性;
4)对端部股线采用平直化处理,绝缘与导体接触紧密;
5)对定、转子股线绝缘、层间绝缘以及主绝缘等效为一个绝缘体;
6)电机各部分浸漆均匀,绝缘良好;
7)定、转子上下层股线施加热源相同,忽略其集肤效应。
1.3物理模型
本文所研究的发电机沿轴向有24个径向通风道,且转子与定子通风道宽度相等且轴向对齐排布。在强迫风机作用下,冷却空气从两端电机端部,对电机进行冷却,从电机流出的热空气经冷却器冷却降温后,再次循环进入电机,构成整个内循环冷却系统,从而带走电机内部的热量,达到降低电机温升的目的。根据该电机通风结构的对称性特征,因此对电机流体场求解时可以采用电机四分之一结构单元,即采用沿圆周方向1/2电机单元、轴向1/2电机单元作为基本求解域。其中计算域内电机端部包含有定、转子端部线棒,转子计算域沿周向分布有27个转子槽,定子计算域沿周向分布有36个定子槽。为了便于研究,将流体域分为两部分,即转子部分的旋转流体域及机壳腔及定子区域中的固定流体域,其物理模型如图1所示。
由图1可知,冷却介质经由电机端部空气域上部进入,冷却电机内部各结构件后,经定子铁心径向风沟流出。为了保证电机内部各结构件得到充分的冷却,在出风口与人风口的交界处放置一个挡风板,挡风板本身不隔热。另外,该区域包含12个径向通风道,从1号到12号依次编号。
同理,为简化计算过程,对于温度场的计算采用如图2所示的轴向1/2、周向1/6的物理模型。
2求解条件
2.1电机基本数据
本文以一台5MW双馈风力发电机为例,该发电机基本参数如表1所示。
根据电机参数对电机电磁场进行计算,得到电机各部分损耗如表2所示。
将电机在额定状态下的损耗作为热载荷,施加在电机定转子铁心及绕组部分,从而对电机进行温度场求解。
2.2边界条件
结合该风力发电机通风结构特点,将电机流体场数值计算求解域的边界条件设置为:
1)人口采用压力人口边界条件,设为1atm;
2)出口采用压力出口边界条件,设为1atm;
3)轴向各截断面均设为Symmetry,周向的各截断面设为Periodic,其他各壁面设为无滑移壁面边界条件。
另外,将电机温度场数值计算求解域边界条件设置为:
1)人口采用速度人口边界条件,速度大小设为0.52m/s:
2)出口采用压力出口边界条件,设为1atm;
3)电机轴向各截断面均设为Symmetry,其余各壁面均设为绝热壁面;
4)将转子区域的流体转速设为电机的额定转速,为1200r/min。
3三维流体场计算及分析
3.1流体场整体分析
发电机转子径向风沟内的槽钢在转子旋转过程中具有离心式风扇的作用,在电机内产生压头,加之强风风机的作用,促进电机内冷却流体不断循环流动带走电机热量。为了全面了解整机内流体流动过程,求出电机内流体流线图,如图3所示。
由图3可知,冷却气体由进风口进入电机端部气腔内,人风口附近流速较低,到气腔后速度逐渐升高,其内部定转子区域流体形态并不完全一样,且与电机底部区域流速相比,靠近电机人口的上层区域流速较大,并且与转子流域相比,定子流域内流速变化更为明显。这是因为电机在稳定运行时,转子处于以恒定转速旋转的状态,而定子与机壳处于相对静止的状态,此时,电机顶部与底部的相对位置对转子流域内影响不大,但对定子流域内流体流动的影响较为显著,致使端部空气域内定转子部分流体流速及空间压力分布不一致。冷却空气进入端部空气域后,经各轴向风道沿轴向流动,受到转子旋转的影响,转子径向通风沟内流体流速较大,受到的压力较大。冷却空气经气隙进入定子径向通风道后,受到沿程阻力的影响,流速显著降低,受到的压力减小。并且定子流域内存在回流,冷却空气在径向风道内发生碰撞,能量损失严重。
提取数值计算结果可以知道,电机计算域内总流量为4.941m3/s,总流量的理论值为4.0788m3/s。鉴于此,可以初步判断,该风力发电机的径向通风结构满足其通风要求。
3.2电机轴向各径向通风沟流场对比分析
电机径向通风沟内冷却气体流量沿轴向长度的增加而发生变化,但是沿轴向方向转子径向风道出口及定子径向风道人口面积均不变,造成冷却气体沿轴向流速将发生变化。为了研究径向风沟内沿轴向方向流体流变特性,分别取1号和12号通风沟中心截面作为采样面,流速分布如图4所示。
由图4可知,从轴向上来看,流体的速度分布规律一致,即1号通风沟流速最大,12号通风沟流速最小,即在轴向方向上,电机中部流量最大,越靠近端部流量越小。
同时可以看出,转子区域流体速度明显大于定子区域。径向长度越大,转子流速也将越大,且迎风面和背风面流速不同,在气隙处达到最大值。针对定子通风槽钢而言,其迎风面与背风面流体流速相差较大,迎风面流体流速较大,但从径向上来看流体速度变化缓慢。这是由于冷却气体从人风口进入端部气腔,而后进入各径向通风沟,由于转子旋转产生的离心力作用,转子区域内风速不断增大,最大值位于转子风道出口与气隙的交界处。定子区域受人风口流速及转子旋转影响较小,故径向上流速变化较小。
为了具体研究径向通风沟内流体流速变化情况,表3给出了各个径向通风沟的最大流速。
为了进一步分析沿轴向方向径向风沟内流体分布特性,取转子径向风沟出口流量及定子径向风沟进口流量,图5给出了定转子通风沟流量分布曲线图。
由图5可知,转子径向风沟出口及定子径向风沟进口流量相差不大,且分布趋势大致相同,均呈现逐渐减小的趋势,1号通风沟处流量最大,转子风沟流量最大值为0.1926m3/s,定子风沟流量最大值为0.19m3/s。
3.3电机径向通风沟流场速度分析
电机定转子通风槽钢对电机内部流体流型演化有很大的影响,根据3.1节和3.2节可知,针对定转子通风槽钢而言,径向长度的不同会导致流体流速产生变化,且迎风面、背风面流体流速也不同。为具体分析定转子槽钢两侧冷却气体分布情况,将采样线设置在1号、6号及12号通风沟内定、转子槽中。
图6中(a)为定子区域AB、EF及CD采样线位置,迎风面处的采样线为AB,背风面处的采样线为凹,槽轭部中间位置为EF,图6中(b)、(c)、(d)为所采样位置处的流体流速变化曲线。
分析图6可得,随着轴向长度增加,3个采样位置的定子通风沟内流速均减小,且最大流速位于1号风沟,最小流速位于12号风沟,但是定子槽钢迎风面相比于背风面而言流速减小趋势不明显。其中,AB处流速最高,CD处流速次之,丑F处流体速度最低。
这是由于槽轭部中间位置两侧空气在定子槽尾部汇集,存在涡流,使定子径向通风沟内流体能量损失较多。另外,流体流速较小的位置出现在定子通风沟人口附近及齿部,定子轭部处的速度急剧增加,导致这种现象的原因是冷却空气在定子齿部处受到定子股线的阻碍,且受转子旋转的影响,相比于迎风面,背风面流速明显下降。当流体到达定子风道出口附近,由于流动区域陡然变大,流速迅速降低。
同样地,对转子区域流体进行相同的研究分析,转子区域采样线为ab、ef及cd,如图7中(a)所示,其中ab为迎风面,cd为背风面。
由图7可知,在轴向上,随着轴向距离的增大,转子各径向通风沟内流速逐渐减小,其变化趋势与定子径向风沟内流体变化趋基本相同,不再赘述。转子风沟内流体流动变化更加激烈,呈非线性变化趋势。在径向方向上,随着径向长度的增加,转子径向风沟内流体与定子内流体变化状态不再相同,而是出现先增大后减小的趋势,在股线区域流速出现拐点,且在背风面cd區域越靠电机端部,流体流速减小越明显。当流体达到风沟出口时,迎风面a6区域的流体流速突然降低,而背风面cd区域的流体突然升高,即流体在该区域均出现拐点,在出口附近,背风面流体流速明显高于迎风面。
4三维温度场计算及分析
基于电机基本假设,根据径向通风电机结构特点及传热特性,建立电机三维物理模型。为节省计算时间,根据电机整体结构的对称性,在电机轴向上选取1/2区域、在周向选取1/6区域作为物理模型,周向上包括12个定子槽和9个转子槽。
4.1主要部件启动温升分析
通过该发电机三维温度场的数值计算,可以得到电机最高温升位于定子绕组上,其数值为93K,小于该电机所采用的F级绝缘材料的温升限值。
为具体分析发电机内部温升分布情况,图8给出了求解域内的温升分布。从图8可以看出,求解域内的最高温升为93K。整体而言,温升变化幅度较大,定子区域的温升较大,转子区域温升较小。电机内部热源所产生的热量由内风路中冷却气体带到机壳外,将传递给机壳。被冷却后的流体首先冷却转子区域,与其进行充分换热,冷却效果强,因此转子铁心温升比定子区域低。
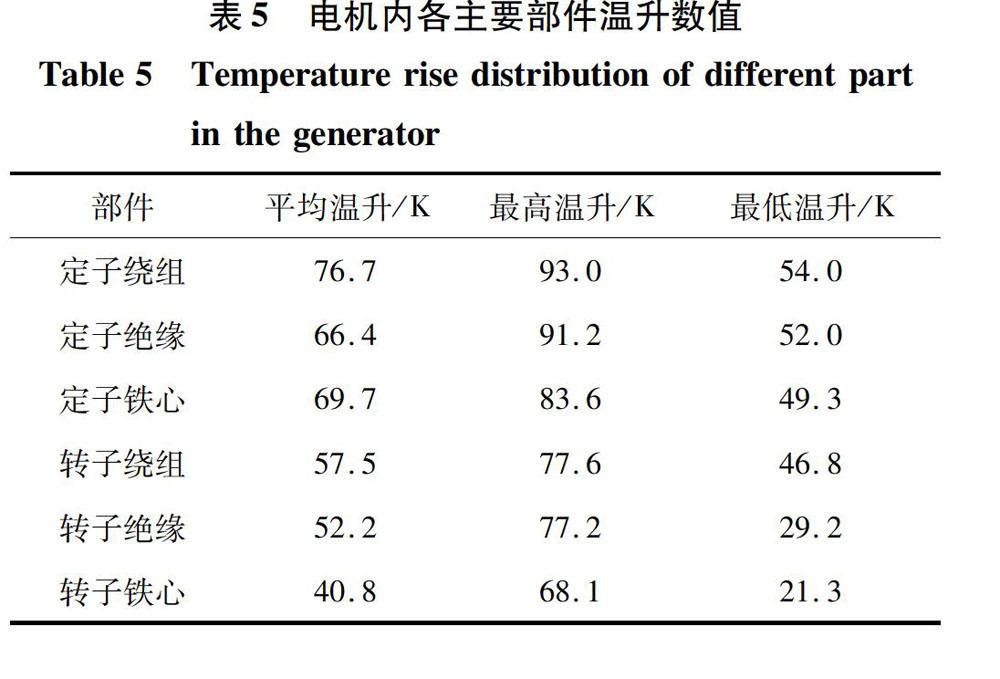
从数据中可以看到,电机不同部位的温升变化梯度很大。定子股线温升最高,转铁心温升最低。电机内温升最大值为93.0K。
4.2电机轴向温升分布规律
图9所示为轴向上各径向切面温升分布图,其中(a)为1号通风沟附近中心截面,(b)为12号通风沟附近截面即定子铁心段中最大温升截面,(c)为电机端部区域截面温升分布。
由图9可以看出,电机最热面在端部铁心处附近。出现这种现象的原因是在电机中心风沟处的冷却气体流量最大,对流换热效果比较好。而电机端部气腔处的冷却气体温升低,散热能力强,所以温升最高的截面出现在电机靠近端部的中间段。
4.3电机径向温升分布规律
图10、图11分别为沿电机转子槽、定子齿中心线处和沿转子齿、定子槽中心线处径向温升分布曲线。
图10中AB段对应转子轭,BC段对应转子槽底垫条,CD段对应转子下层绕组,DE对应转子绕组的层间绝缘,EF对应转子上层绕组,FG表示转子槽楔的径向高度,CH表示气隙径向厚度,HI表示整个定子铁心的径向长度。
图11中AB段表示转子铁心轭径向长度,BC段表示转子铁心齿部径向长度,CD段表示气隙径向厚度,DE段表示定子槽楔和上层股线的径向高度,E处为定子上下层股线间的层间绝缘,EF段表示定子下层股线段,FG表示槽底绝缘的径向宽度,GH段表示定子轭部径向高度。
由图10可知,绝缘的导热系数小因而散热效果差,所以在BC段温升发生突变。在转子区域,上层绕组的温升高于下层绕组,这是由于冷却空气在电机内部流通时先到达下层绕组,冷却效果较好。在气隙处温升变化剧烈,迅速下降后又迅速上升。结合图11可知,周向不同位置处气隙的温升几乎没有变化。而温升曲线并不是垂直变化,这是由于靠近热源处的冷却气体被加热。
由图11可以看出,定子的温升较高,转子铁心的温升较低。定子下层股线温升最大,达93K。产生这种现象的原因有两方面,一为绕组在发电机稳定运行时,产生的电磁损耗大于其他部件。其次,冷却后的气体后先流过转子通风沟,之后流入定子通风沟,冷却效果下降,故转子区域的温升较低。
5结论
本文采用有限体积法对具有密闭循环冷却系统的径向通风电机流体场及温度场进行数值研究,揭示了流体流变特性及传热规律。得出以下结论:
1)通过计算得电机所需冷却风量为4.0788m3/s,本文中总风量达4.941m3/s,因此可知,电机的冷却系统设计是合理的,温升值满足电机采用的绝缘等级要求。
2)在轴向方向上,电机中部流量最大,计算域内转子风沟流量最大值为0.1926m3/s,定子风沟流量最大值为0.19m3/s,而越靠近端部流量越小;在径向方向上,随距离的增加,风沟内流体呈非线性变化,在定转子股线附近及风沟出口处流速变化较大且呈现拐点,最大流速点位于气隙处,最大值为74.67m/s。流体进入定子径向风沟后,出现回流,流速降低;
3)电机各个部位的温升变化梯度很大,定子区域的平均温升及最大温升均较高,其中繞组温升最大,其次为绝缘,温升最低位于定子铁心处;转子区域温升相比于定子区域而言较低。计算所得温升满足设计要求,可以判断流场流量可行。
4)从径向上看,温升变化剧烈,定子部分温升较高,最高温升点位于定子绕组,为93K,转子区域温升较低。从轴向上看,温升分布大致相同,呈现先下降,然后上升,最后在端部降低的趋势。

