襟翼非对称故障模式建模与仿真研究

(中国商飞上海飞机设计院，上海 201210)

根据民机事故调查，飞机起飞和着陆阶段的事故率高达68%。高升力系统(即襟翼和缝翼控制系统)负责在这两个阶段提供增加升力、减小阻力、防止失速等功能，是飞机的安全关键系统之一。目前，国内对高升力系统的研究刚起步，尚无关于高升力系统建模研究的相关论文，仅有对波音777飞机高升力控制系统架构的介绍[1]，及对其齿轮旋转作动器的类型和特性的研究[2]。

针对襟翼非对称问题，详细分析其故障原因，建立Simulink襟缝翼控制系统仿真模型，并基于所建立的模型，设计襟翼非对称故障注入方法，实现襟翼不对称故障场景仿真。

1 襟翼系统简介

民用飞机在副翼上具有辅助操纵翼面，即前缘缝翼(Slat)和后缘襟翼(Flap)，在左右机翼上对称分布。飞行员依据飞行阶段和飞行条件，操纵襟/缝翼手柄到合适卡位，控制缝翼向下前伸和襟翼后退偏转，改变机翼弯度和面积，增加飞机起飞时的升力和着陆时的升力和阻力，缩短飞机起飞和滑跑距离。

2 系统建模

襟翼系统包括控制和作动两个部分。控制部分包括：襟/缝翼控制手柄、襟/缝翼计算机、位置传感器、倾斜传感器、能量驱动装置(含液压马达)。作动部分包括：翼尖刹车、扭力管、角齿轮箱、旋转作动器等。

2.1 控制手柄建模

控制手柄建模为四冗余通道的电位计，将手柄位置转换为电信号，再由计算机解算为对应的手柄卡位[3]。襟/缝翼手柄卡位包括：4，3，2，1，0。

2.2 襟/缝翼计算机建模

襟/缝翼计算机(FSECU)为襟翼收放速度和位置控制和故障监控的控制器。襟/缝翼收放位置控制采用双闭环PID控制方式，内环控制PDU液压马达速度，外环控制马达速度改变传动轴速度[4,8]。系统运动时，位置传感器将实际翼面位置反馈给计算机，构成控制闭环，如图1所示。

图1 襟/缝翼控制原理

2.3 机械传动系统建模

襟/缝翼传动机构模型分为3个部分：能量驱动单元(PDU)、左侧翼面系统和右侧翼面系统，如图2所示。

图2 液压机械设备建模

PDU根据液压供压和回压、襟翼电液伺服阀(EHSV)电流、翼面传动系统反馈的左右扭力管角度和速率计算襟翼压力输入、马达位置、速率、马达传感器的位置和速率、输出左右侧扭矩。翼面传动系统根据PDU输出扭矩，翼尖刹车(WTB)指令计算出翼面解算器角度和翼面位置角度。

2.3.1 液压机械驱动建模

PDU是襟翼系统的控制部件，接受计算机的电液阀命令，控制液压流量实现双余度液压马达转速和方向控制，并输出扭矩，经叠加后传递给左右侧襟翼系统[5]。

① 电液伺服阀为两级偏转射流阀，提供与输入电流相应的流量。根据电液伺服阀EHSV电流命令，计算EHSV阀芯位置，进而获得入口阀芯面积。

② 液压马达为直立式固定流量泵，采用可逆轴向活塞泵类型。根据阀芯面积计算马达流量：

(1)

式中，μ为流量系数，与阀门形状有关；A,P,ρ分别为阀芯面积、阀前后压差、液压流体密度。

③ 由液压马达流量计算马达的压差，获得马达输出扭矩值。假设压差为P，马达容量为ηm，马达扭矩为Tm计算公式为

Tm=P×ηm×(1-ηv)

(2)

式中，ηv为马达效率，可根据压差和马达速度查表获得。

④ 根据马达扭矩计算马达转速和马达转角：

(3)

式中，Tm,Tb为马达扭矩和刚度扭矩；Tf为动态摩擦力；m为马达惯性；x为马达角度。

Tb=(θm1+θm2-θcλ)k+(ωm1+ωm2-ωcλ)ε

(4)

式中，λ为PDU比，PDU中包含两个马达作为襟翼或缝翼的双通道驱动；θm1和θm2分别为马达1和马达2角度；ωm1和ωm2分别为马达1和马达2速度；θc和ωc分别为中心角度和速度；k为马达刚度；ε为阻尼；Tc为中心扭矩，计算公式为

Tc=Tb×λ

(5)

⑤ PDU齿轮箱转动角度和速度计算公式为

(6)

式中，TsL为左侧刚度扭矩；TsR为和右侧刚度扭矩；x为中心角度；Tc为中心扭矩；μ为驱动效率。

左侧传动轴扭矩为

(7)

式中，f为刚度；ε为阻尼系数。

⑥ 马达速度传感器输出计算公式为

P=Pm1×Cs+αI

(8)

式中，Pm1为马达1位置；Cs为传动轴的传动比；αI为位置传感器的初始角度。

2.3.2 翼面系统

翼面系统包括各站位扭矩限制器、旋转作动器(GRA)、翼尖刹车和翼尖位置传感器。建模时，考虑系统效率、静态动态摩擦、惯性刚度的影响。

① 根据PDU提供的左侧驱动扭矩TL、上下游效率计算驱动扭矩和刚度扭矩。驱动扭矩等于左侧驱动扭矩TL，刚度扭矩F计算公式为

F=c(ωT-ωD)+k(θT-θD)

(9)

式中，c为阻尼系数；k为刚度；ωT为轴速度；ωD为下游轴速度；θT为轴角度；θD为下游角度。对L1、L2站位，L3、L4站位就是下游。

② 根据作动器载荷、动静摩擦、黏性力矩、速度门限、惯性、GRA，计算轴角度和速度：

(10)

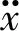
③ 根据轴速度和轴角度计算站位载荷。

(11)

式中，Lact为实际载荷；c为驱动因子；LFlapL1为襟翼站位L1载荷；TEnd为终端扭矩；RGRA为作动器齿轮比；GDown为GRA下游齿轮箱的齿轮比。

④ 轴角度通过GRA齿轮比和传动比换算为GRA运行角度，经函数拟合为襟翼翼面角度。

3 襟翼非对称故障注入

襟翼对称分布在机翼左右侧的后缘，多块翼面联合伸出或收回到同一角度，传动线系距离较长，翼面运动时间长，因此常发生襟翼非对称故障，即飞机左右侧机翼的襟/缝翼的翼面位置不一致，并超过门限值[6]。故障源包括：襟翼翼面间断开或PDU内断开导致襟翼左右两侧展开不一致，以及作动器与下游部件断开，翼面和下游部件断开，扭力管断开，角齿轮箱断开等。这些会对飞机结构载荷造成影响，严重时可破坏机翼翼面，造成飞机事故。

基于上述模型，设计故障输入端口，用故障代码表示故障类型，用故障向量表示故障所需定义参数。如图3所示，首先模型判断故障输入为非对称故障，设置PDU断开信号，改变对应侧PDU输出的扭矩，使两侧翼面运动角度产生差异，导致在FSECU内触发非对称故障监控器。

图3 非对称故障注入流程

4 襟翼非对称故障仿真

根据前述系统分析，使用Matlab/Simulink建立襟翼控制系统仿真模型，设置仿真频率为480 Hz，时间120 s，采用算法ODE4。设置液压供压3000 psi，回压50 psi，电源28 V直流，空速为60节，迎角为1°，高度5000 ft，轮载为0。操纵襟/缝翼手柄从0卡位伸出到4卡位。襟/缝翼手柄输入如图4所示，从4卡位依次收回到3卡位、2卡位、1卡位，最后到0卡位。

图4 襟/缝翼手柄输入

故障注入向量设定为左侧襟翼非对称，在25 s时，单侧襟翼被PDU锁住，右侧襟翼继续运动，直至左右侧襟翼角度偏差达到设定阈值以上，襟翼监控器被触发。倾斜监控门限设定为3°。图5和图6分别为左襟翼非对称故障仿真图和状态位图。

图5 左襟翼非对称故障仿真

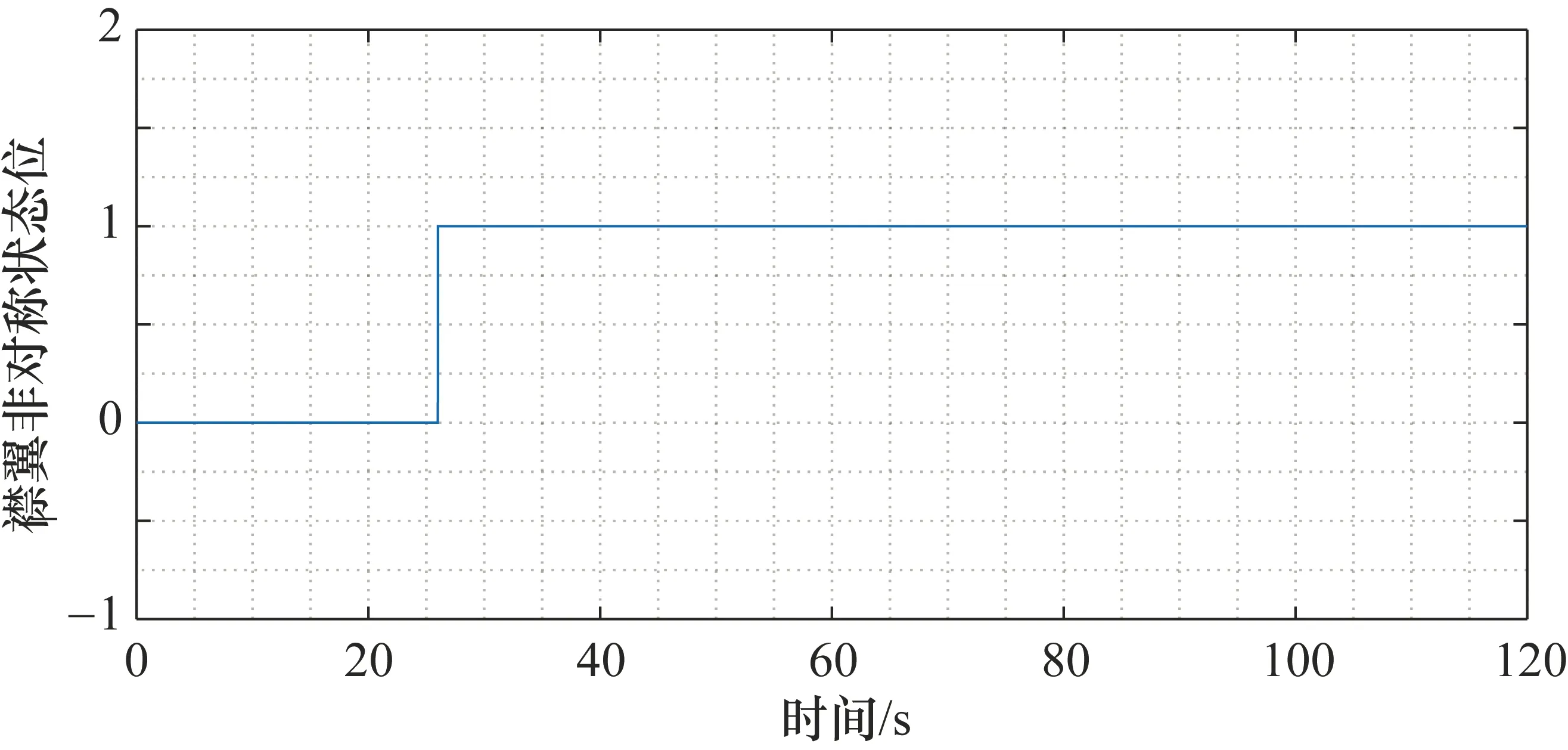
图6 左襟翼非对称故障状态位

从图5和图6中可以看到，当故障代码设定为左侧襟翼非对称故障，运行襟/缝翼控制系统故障仿真，从仿真结果可以看出，左侧襟翼和右侧襟翼位置在25 s左右开始出现了偏差且大于3°，触发襟翼非对称监控器，并置监控器为1。仿真结果表明：所设计的襟/缝翼控制系统仿真模型可满足系统仿真需求，且襟翼非对称故障注入方法简单易行，便于后续对襟翼非对称故障的进一步深入研究。

5 结束语

针对民用飞机襟翼非对称故障问题，基于襟翼控制系统原理，采用Matlab/Simulink建立数字仿真模型，并设计一种襟翼非对称故障注入仿真方法。最后通过左侧襟翼非对称故障的仿真结果，表明襟翼控制系统模型合理有效，故障注入机制设计可行，可用于深入研究襟翼非对称故障问题。