基于MFCC的频谱重构实现音高估计和发声分类

(杭州电子科技大学 新型电子器件与应用研究所，浙江 杭州 310018)

梅尔频率倒谱系数(MFCC)广泛用于语音识别、说话人识别和其他语音处理系统。近年来，有一种新兴的方法可以预测MFCC矢量的基频和发声，这使得语音信号能从分布式语音识别(Distributed Speech Recognition,DSR)后端的MFCC矢量流中重构[1-3]。该算法通过对基频和MFCC的联合密度建模来预测基频。该方法基于高斯混合模型(Gaussian Mixture Model,GMM)，并利用隐马尔可夫模型(Hidden Markov Model,HMM)将一系列依赖于状态的GMM连接在一起。特定说话者的HMM-GMM预测器显示出良好的结果。然而，非特定说话者的HMM-GMM会产生很多错误。此外，HMM-GMM预测器需要一组基于单音的HMM和一组特定状态的GMM训练。训练的预测器被指定为某种语言，并且必须用其他语言重新训练。

量化MFCC的低比特率语音编码方案在文献[4]和文献[5]中被提出，从MFCC重构了语音波形但没有涉及音高和能量。重构通过Moore-Penrose伪逆从MFCC恢复幅度谱，然后利用最小二乘估计，逆短时傅里叶变换幅度算法重构语音帧。此外，近年来有学者提出了一些新颖的音高检测方法。一种名为具有幅度压缩的音高估计滤波器(A Pitch Estimation Algorithm Robust to High Levels of Noise,PEFAC)的算法利用非线性幅度压缩来衰减窄带噪声分量，并利用梳状滤波器来衰减对数下频率功率谱平滑变化的噪声分量[6]。在文献[4]～文献[6]的新方法研究的推动下，通过MFCC反演操作重构语音频谱和倒谱，并利用倒谱/频谱估计音高。

所提出的算法通过梅尔加权函数利用Moore-Penrose伪逆从MFCC重构倒谱/频谱。利用重构的倒谱，可以直接从峰值估计音高，而由于重构失真可能存在大的误差。提出了一种组合非线性幅度压缩和对数频率功率谱域滤波器的方法，以减少误差。利用滤波后的功率谱和音高的相关性，提出了一种基于GMM的音高估计方法，以获得更可靠的音高。此外，还提出了一种发声分类方法。所提出的方法的主要优点是特征提取，其使用经过重构和滤波的幅度谱而不是原始的MFCC矢量。与以前的工作[1-3]相比，所提出的方法是一种非特定说话者/语言的预测器。

1 频谱重构

MFCC被定义为特殊倒谱，在对数运算和离散余弦变换(Discrete Cosine Transform,DCT)之前将一组加权函数作用于功率谱。这种加权函数基于人类对音高的感知，最常见的是以梅尔克度(Mel-Scale)[4]，即文献[5]中的一组三角形滤波器的形式实现。其中第t个语音帧St(n)的梅尔倒谱M的计算公式为(省略下标t以简化符号)

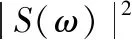
(1)

式中，wm为梅尔加权函数；S(ω)为S(n)的离散傅里叶变换(Discrete Fourier Transform,DFT)。在式(1)中具有梅尔加权的功率谱可以以矩阵形式表示为

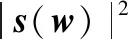
(2)

式中，y为J×1的向量(J为梅尔滤波器的数量)；Wm为J×L的加权矩阵(L为帧长度)。

在式(1)中通过应用梅尔标度加权会使频谱信息丢失，而其他操作如离散余弦变换，求对数和平方根都是可逆的。为了逆梅尔加权，可以采用最小欧几里德范数的解，即

(3)

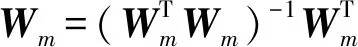
2 基于频谱重构的音高估计和声音分类

2.1 基于频谱滤波器的音高估计

文献[2]的作者利用MFCC和基频(即音高)的相关性，用GMM预测音高。同时，发现重构幅度谱与音高之间的相关性更高。表1给出了使用TIMIT训练子集计算的不同矢量(MFCC，重构幅度谱和滤波频谱)与音高之间的相关性。

表1 音高与不同向量(MFCC、重构幅度谱、滤波频谱)之间的相关性

表1的结果表明，重构幅度谱和音高之间的相关性高于MFCC。与MFCC矢量相比，幅度谱包含更多关于音高频率的信息。 因此重构幅度谱更适合于基于GMM的音高估计和发声分类。

事实上，语音信号总是被各种噪声干扰或卷积，并且幅度谱的谐波峰值将通过成帧窗口加宽。为了减少重构失真引起的误差，使用一种音高估计方法，结合非线性幅度压缩来衰减窄带噪声分量，并采用对数频率功率谱域滤波器来衰减平滑变化的噪声分量[6]。该算法描述如下。

③ 通过式(4)压缩功率谱密度(Power Spectral Density,PSD)：

(4)

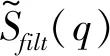
④ 通过以下公式过滤压缩PSD。

h(q)=β-log(γ-cos(2πeq))

(5)

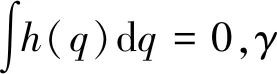
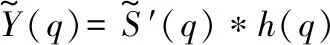
(6)

2.2 基于GMM的音高估计

为了更准确地估计音高，利用滤波后的PSD和音高的相关性。特征向量Φ表示为

Φ=[Ω，f]

(7)

通过GMM构建特征向量Φ。从训练集中，使用期望最大化(Expectation Maximization,EM)算法产生一组K高斯聚类。Φ的概率密度函数(Probability Density Function,PDF)为

(8)

每个K聚类由先验概率πk和高斯PDFN(Φ)表示，具有平均向量μk和协方差矩阵Φk。

(9)

使用著名的Linde-Buzo-Gray(LBG)算法找到EM训练的初始聚类位置，最大EM聚类迭代为100。在实验部分中讨论K的选择。

(10)

后验概率hk(Ωi)为

(11)

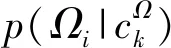
2.3 清音/浊音分类

音高估计应该仅应用于重构表示有声语音的频谱。在文献[2]中，通过扩展HMM-GMM音高预测器来实现，其需要一组基于单音的HMM和一组状态特定的GMM训练。 训练好的预测器被指定为某种语言，并且必须以其他语言进行再训练。

提出了一种低复杂度的语音分类算法，该算法是通过基于GMM的模型实现的。该模型利用帧平均功率和滤波频谱峰值的相关性，其包括更多潜在的发声信息。

从一组训练数据中提取特征向量Ψ：

Ψ=[s,χ]

(12)

式中，s=logμpsd,χ=Σpitch/μpsd。其中,μpsd为式(4)中压缩PSD的平均功率值，Σpitch为式(6)中3个候选音高的总和。

对于浊音/清音分类器有两个GMM，一个用浊音矢量Ψv组成的训练集进行浊音建模，一个用清音矢量Ψμ组成的训练集进行清音建模，建模方法与文献[8]中描述的相同。浊音的帧的概率为

P(v)=(1+exp(pu-pv))-1

(13)

式中，pu和pv分别为清音GMM和浊音GMM的后验概率。

对于输入特征向量Ψi，用GMM计算pv(ψi)和pu(ψi)的后验概率，然后通过式(13)计算被发声的概率。如果P(v)>ε(ε是阈值，设置为0.5)，则该帧被分类为浊音，否则被分类为清音。

3 实验结果

下面将评估音高估计和发声分类的结果。使用TIMIT数据库进行培训和测试。每个句子的持续时间约为3 s，下采样频率为8 kHz。语料库使用汉明窗框架成200个样本(25 ms)，帧移位为80个样本(10 ms)。

3.1 频谱/倒谱重构结果

将MFCC反变换到频谱是一项具有难度的任务，因为式(2)中的梅尔加权函数会造成大量信息的丢失，而式(3)只是近似解。很明显，梅尔滤波器越多，幅度谱的信息就越少。 在本文中，梅尔滤波器的数量是23，就像DSR前端一样[9]。考虑到反变换，所有23个MFCC都被保留，而在DSR中舍去了10个高阶系数。

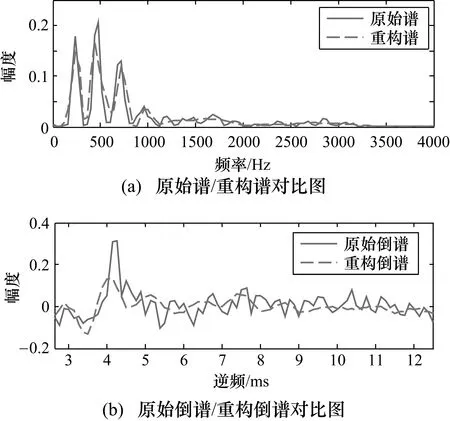
图1 MFCC对浊音语音帧的频谱/倒谱重构

图1显示了MFCC的频谱和倒谱的重构结果。图1(a)比较了原始谱和重构谱，从中可以看出式(3)的原始和近似解之间只有微小的差别。图1(b)展示了原始和重构的倒谱，峰值是候选音高。

3.2 音高估计结果

音高估计结果如图2所示。

图2展示了利用MFCC重构频谱/倒谱的音高估计结果。首先直接估计具有重构倒谱峰值的音高(即ceps.线条)。然后利用非线性幅度压缩和对数下频率功率谱滤波器来减少误差(即filt.线条)。

图2 估计结果与参考音高轮廓的对比

所提出的基于GMM的音高估计器利用经滤波的PSD和音高的相关性，可以得到更可靠音高估计结果(即GMM线条)。由于音高的频率范围是60～400 Hz，帧长度是200，所以候选音高在式(6)输出的31～62之间。因此式(7)中Ω的尺寸为32(即GMM线条)。参考音高轮廓用ref.线条表示。在实验中，GMM[10]聚类的数量是32，在下面的评估中将讨论参数的更多细节。

图2展示了直接利用重构的倒谱峰值(即ceps.线条)估计音高可以跟踪参考音高轮廓，但由于倒谱重构失真所以存在一些误差。可以通过在对数下对频率进行压缩和过滤(即filt.线条)从而获得更好的结果。采用GMM的MAP音高估计结果与参考值完全匹配。

(14)

在音高估计之前，应使用第3.3节中描述的方法将帧分类为浊音或清音。使用百分比发声分类误差EC来测量准确度，其中N是测试集的总帧数，NV/U和NU/V是可分辨清音和浊音帧的错误分类数量。

表2 清音/浊音分类误差EC

表2显示了不同GMM群集的分类误差，清音和浊音GMM群集的数量相等。从结果可以看出随着GMM聚类数量的增加，分类误差减少了。但是当数量增加到16，准确性却没有进一步提高，这可能是因为过拟合。

对于进一步浊音帧，使用百分比音高频率误差Ep来测量音高预测精度，即

(15)

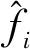
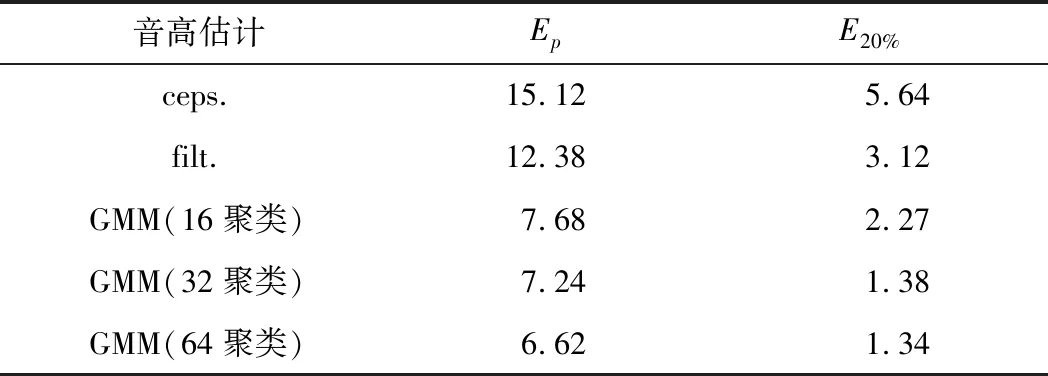
表3 音高估计误差Ep和E20%

音高估计误差与3种方法的比较如表3所示。具有重构倒谱峰值(ceps.)的音高估计器表现一般。利用非线性幅度压缩和对数下频率功率谱滤波器(filt.)，在精度上有所提高。基于GMM的估计器展现出高精度，并且增加聚类数可以减少估计误差[11]。

4 结束语

利用梅尔频率倒谱系数(MFCC)重构频谱，提出了一种新的音高估计和声音分类的方法。所提出的算法通过梅尔加权函数来构造来自MFCC的具有Moore-Pemose伪逆的频谱。重构的频谱在对数下进行频率压缩和过滤。通过高斯混合模型(GMM)对音高频率和滤波器频谱的联合密度建模来实现音高估计。基于GMM的模型也可以实现发声分类，测试结果表明，超过99%的语音帧可以被正确分类。音高估计的结果表明，所提出的基于GMM的音高估计器具有高精度，TIMIT数据库上的相对误差为6.62%。