中等规模中继协作通信系统波束成型算法研究

(陕西国际商贸学院 信息工程学院，陕西 西安 712000)

目前，关于大规模和小规模情况下增大和速率的波束成形算法的研究较多，文献[1]提出了一种分支定界法来解决单运营商情况下的和速率最大化波束成形矩阵的设计问题，但其在天线众多的情况下具有过高的计算复杂度。文献[2]提出了一种基于半定松弛模型的多项式时间迭代方法来解决此问题。文献[3]和文献[4]提出了两种基于一维和二维的启发式算法，文献[5]提到了基于ZF(Zero Forcing)和最大比合并MRC(Maximum-Ratio Combining)的方法。上面提到的方法大部分仅仅适用于小型MIMO(Multiple-input Multiple-output)系统[6]。大规模MIMO概念[7]地址使用大量的收发转换天线来改进性能，尤其是针对超大规模的MIMO系统，即当天线数量在特定情况下发散到无穷多时，使用ZF[8]和MRC[9]来实现和速率最大化几乎可以达到最佳效果。但ZF/MRC接近最优的情况一般不适用于中等规模的MIMO系统。

1 系统模型

1.1 系统模型设计

本文研究的MIMO AF(Amplify-and-Forward)双向中继网络由N个天线、L个(通信)运营商以及来自不同运营商的用户终端对组成，在中等规模MIMO中使用较为广泛。假设用户终端是单天线的，第l个运营商的第k个用户和中继之间的平坦衰落信道用{hk,l}表示。中继接收到的信号可以表示为

(1)

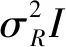
(2)

式中，G∈CN×N是需要被设计的中继放大矩阵。假设中继和用户之间是双向通道，则第l个运营商的第k个用户接收到的信号yk,l为

(3)

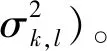
(4)

式中，ηk,l为第l个运营商的第k个用户的SINR(Signal to Interference plus Noise Ratio)，其表达式如下：

(5)

式中，g=vec(G);φk,l，γk,l，Δk,l的定义为

(6)

假设利用信道知识可以完全消除自干扰。在式(5)、式(6)对SINR的定义中自干扰已经被忽略。本文设计的方法即便没有这种假设也能被应用在和速率最大化问题中。和速率最大化被中继中可得到的全部能量PR所约束，即

(7)

也可写成关于g的表达式，gHCg≤PR，其中，

(8)

目标是设计出AF放大矩阵G来最大化和速率Rsum，因此L个运营商MIMO AF中继网络的设计问题即和速率最大化，可被看作如下问题：

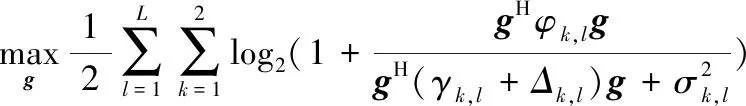
(9)

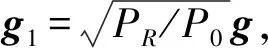
(10)

其中Bk,l，Ak,l的定义如下：

(11)

1.2 MaMi算法设计

式(10)中考虑缩放比例的目标函数是不变的，因此可以求解无约束问题，对解g进行缩放使其满足约束条件gHCg=PR。本文使用MaMi技术来解决式(10)中的非凸设计问题。MaMi是一种迭代手法，用来获得一般最大化问题的解[10-11]。

(12)

MaMi的每一次迭代都可以分两步进行(见图1)，下面以第k次迭代为例进行说明。

(13)

其中z(k-1)是z在第(k-1)次迭代的值。

② Maximization：求解最优化问题。

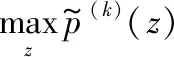
(14)

得到z(k)。

现在考虑式(10)的等价形式：

(15)

下列不等式是由对所有x成立的log(x)的凹性控制的，x0∈R+：

(16)

(17)

另外，用上述minorizer结果(忽略常数)来代替式(15)中的-log(gHBk,lg)，可得到下列第(k+1)次迭代的最大化问题：

(18)

受关于半定松弛的大量文献的启发，注意到在式(18)中将X=ggH作为优化变量，同时丢掉秩为1的约束条件，那么式(18)中的每一次迭代都可以获得一个凸的替代[12]。一旦获得解X，优化矢量g可以由X合成，这对秩为1的解X是无法保证的，故此方法存在合成损失[13]。另外，应用松弛定理会迭代求解最大化凸行列式问题，其具有很高的计算负担。后续设计了一种计算高效的方法，它能增加每一次迭代的目标值，并且保证g的一阶最优条件。使用下列引理继续寻找作为g的函数log(tr{Ak,lX})的minorizer。

引理1：对任意的正定矩阵T，C，令s(x)=-log(xHTx)，xHCx=P，其中T,C∈CN×N,P∈R+，可得到：

s(x)≤s(x0)+R(bH(x-x0))+(x-x0)HU(x-x0),∀x,x0

(19)

其中,

(20)

式中,w1为T的主特征向量，∈>0任意给定。MaMi算法示意图如图1所示。

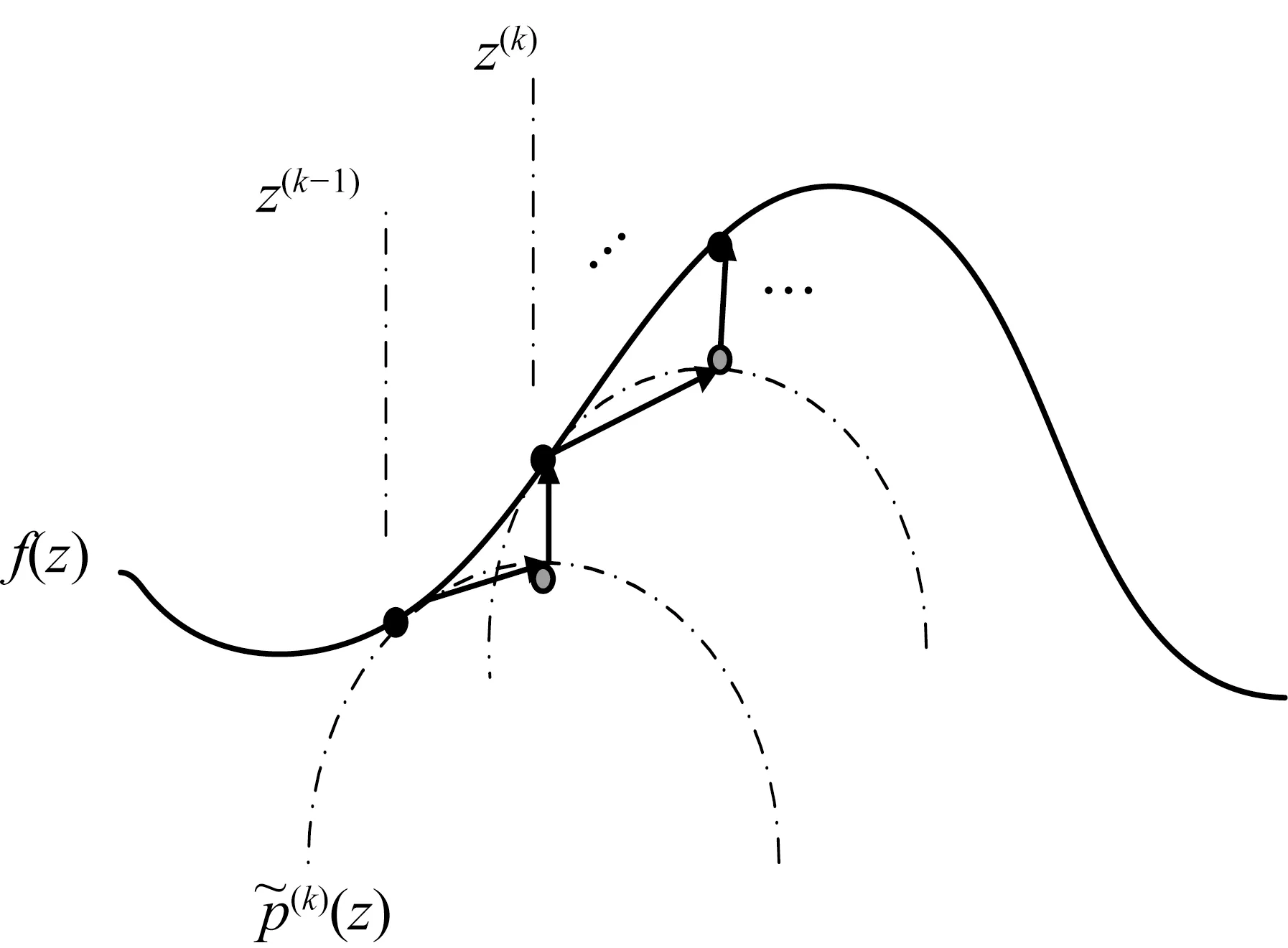
图1 MaMi算法示意图

假设每一次迭代中都有gHCg=PR。可观察到，对任意给定的g0，使用上述引理，可获得log(gHAk,lg)的minorizer：

(g-g0)HUk,l(g-g0)

(21)

式中，矩阵bk.l和Uk,l与Ak,l有关，可将式(20)代入到引理中计算得到(见式(23))。基于式(18)和式(21)，考虑到关于所提出方法的第(k+1)次迭代得到的g的下列准则的minorizer：

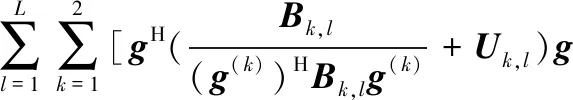
(22)

其中，

(23)

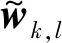
(24)

其中,

(25)

(26)

该矩阵是具有正标量的单位矩阵I的缩放版，所以Bk,l≥0,Uk,l≥0。因此，矩阵Q(k)在每一次迭代中都是正定的，式(24)中关于g的问题是严格凸的。可以通过解线性方程组2Q(k)g+q(k)=0来获得唯一解，即

(27)

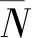
表1 中继波束成形使和速率最大化的方法

2 改进的正交零空间投影MaMi算法

前面介绍的MaMi算法只适用于目标函数是单峰的情况，较为理想化，如果目标函数是多峰的，该方法得到的最大值为局部最大值。为了获得全局最优解，对MaMi算法进行改进，如图2所示，假设MIMO AF RS中和速率函数有可能是多峰函数，使用零空间正交投影方法在多个方向上使用MaMi算法得到多个最优解，然后优中取优，以求出和速率性能相对最好的波束成形矩阵，具体改进如下。

图2 改进MaMi技术的描述

应用MaMi算法得到使和速率最优的波束成形矩阵：

(28)

考虑到多峰情况，将g在零空间向量上进行平移得到新的g，记为

(29)

式中，I为单位矩阵；w为随机向量；将g′作为初始向量，在新的方向上使用MaMi算法求得使得和速率最大的新的最优解g，与原g进行比较，选择和速率更大的保留。具体步骤如表2所示。

表2 使用改进MaMi算法来最大化和速率的步骤

3 仿真结果与分析

前面探讨了MaMi算法改进的方法和具体的实现步骤，为了观察改进后算法的收敛性，仿真给出其在信噪比分别为0 dB，10 dB，20 dB条件下的和速率随迭代次数的变化关系。仿真环境为用户终端对数K=8，每用户天线数M=1，中继天线数N=16。结果如图3所示，在0 dB和10 dB条件下，迭代两次即可达到收敛，在20 dB条件下，迭代5次也基本达到收敛，可见MaMi算法收敛速度快。

图3 MaMi算法和速率随迭代次收敛曲线

由于奇异值分解(Singular Value Decomposition，SVD)需要用户端充分完美协作，此种协作在实际通信系统无法实现，SVD仅能提供系统和速率性能上界，因此本文采用SVD算法作为对照组进行试验。图4显示了MaMi、改进正交零空间投影MaMi与SVD 3种算法在SNRRS=SNRMS条件下和速率随SNRMS的变化曲线。从图中可以看出，所提出的改进正交零空间投影MaMi算法，在中高信噪比区域和速率性能优于MaMi算法，在低信噪比区间和速率性能稍优于MaMi算法，但是离SVD给出的上界仍然有一定差距，考虑SVD需要用户端充分协作，在实际系统不可实现，所提改进算法有相当实用性。

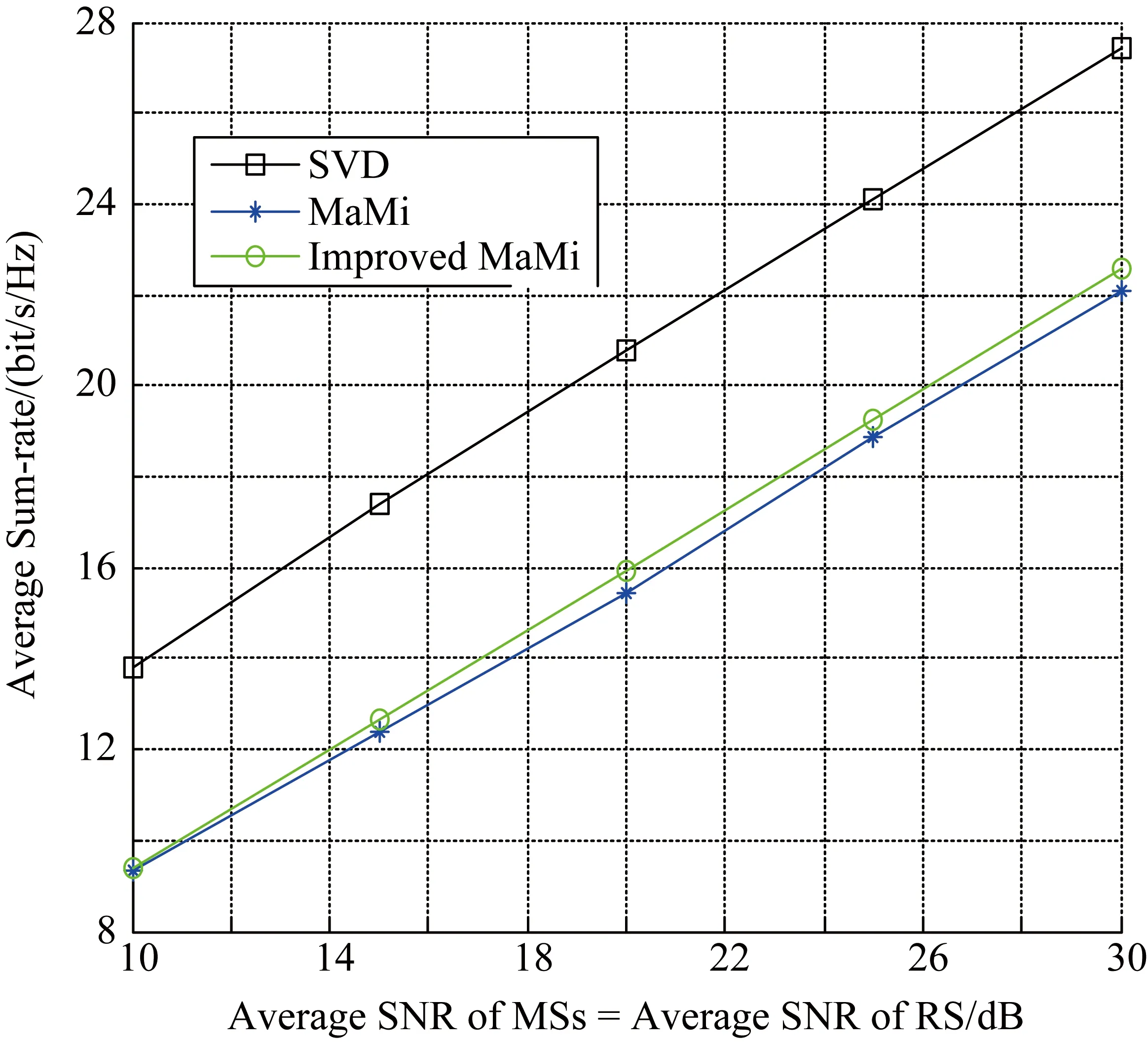
图4 不同波束成形算法下和速率随SNRMS

图5绘制了MaMi、正交零空间投影MaMi与SVD 3种算法在SNRRS=SNRMS条件下误码率随SNRMS的变化曲线。由图5可知，所提出的改进正交零空间投影MaMi算法，在中高信噪比区域，误码率性能优于MaMi算法，在低信噪比区间，误码率性能稍优于MaMi算法，与和速率性能基本一致。

图5 不同波束成形算法下误码率随SNRMS

4 结束语

研究了通过迭代求解优化问题的MaMi算法，考虑到目标函数多峰的情况，提出使用正交零空间投影对MaMi算法进行改进，得到了更优的和速率和误码率性能。该改进算法同样可以应用在其他优化问题中。在用户单天线情况下，将波束成形矩阵设计问题等效为优化问题，传统的算法只能得到局部最优解，提出改进的正交零空间投影MaMi算法，尽可能找到和速率的全局最大值。对两种算法性能进行仿真得到结论：在中低信噪比情况下，改进后算法在和速率以及误码率性能均优于原始的算法。