基于CS理论的24脉波整流器开路故障诊断方法
2
(1.兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070; 2.甘肃交达工程检测科技有限公司,甘肃 兰州 730070;3.喀什大学 教育科学学院,新疆 喀什 844000)
24脉波整流器自出现以来一直被广泛地运用,是当前城市地铁和轨道交通中的关键设备之一。然而在实际使用过程中,该整流器的功率开关器件(晶闸管)较易损坏。当晶闸管发生开路故障时,整流电路会继续工作,致使输出电压波形发生严重畸变,而负载也处于非正常运行状态,与此同时产生的谐波也会对整个电网造成冲击 。本文仅针对晶闸管开路故障进行研究(不考虑短路故障)。
目前,国内学者对24脉波整流器的开路故障研究,只有闫淑群[1]等人通过对电压故障数据运用FFT变换和归一化等方法处理和分析之后,建立故障特征向量,实现故障分类识别。此方法待处理的数据量太大,故障诊断的速率慢和诊断准确率不高。另外,针对牵引变流器[2]、风电变流器[3-4]、变频器[5]、VIENNA整流器[6]等的开路故障问题,国内学者进行了研究并取得了一定成果。由于以上整流器故障检测和诊断方法都建立在Nyquist采样定理的基础上,要求采样频率均在原始信号频率的2倍以上,并且待处理的数据量非常大,严重影响了故障诊断的准确率和诊断速度。
2006年,Donoho等人提出压缩感知(Compressed Sensing,CS)理论[7-8]。该理论突破了传统Nyquist采样定理的瓶颈,其采样频率远低于传统采样频率限制,同时还将压缩和采样同时进行,实现对原始信号的准确重构。张晓东[9]等人将坐标变换和压缩感知理论相结合,将三相电压信号进行压缩处理,取得了较理想效果。但其仅仅对三相电压信号进行了压缩处理,并没有对故障进行诊断和识别。
因此,本文结合压缩感知理论,针对24脉波整流器开路故障输出的电压信号,首先利用冗余字典和高斯测量矩阵对故障电压信号进行稀疏表示和测量;然后,采用正则化自适应匹配追踪(RAMP)算法对压缩采样信号进行重构;最后,对重构得到的稀疏向量S′进行六种特征参数的提取,将其作为 BP神经网络的输入,实现故障诊断和识别,证明了所提方法的可行性和有效性。
1 压缩感知原理研究
压缩感知理论主要包括3个部分:信号的稀疏表示,信号的非线性测量表示和信号的重构算法设计,运用该理论的条件是信号具有可压缩性或稀疏性[10-13]。
如果一维信号XN×1在稀疏域是K-稀疏的(K< Y=ΦX=ΦΨS=ΘS (1) 式中,Θ=ΦΨ,称为传感矩阵;S为稀疏向量。得到压缩测量值YM×1,则通过求解如下L0-范数优化问题就可以高概率地重构原信号X′=ΨS′。 S′=argmin‖S‖0(s.t.Y=ΦΨS) (2) 式中,‖S‖0为S的0范数;Φ为测量矩阵;Ψ为稀疏矩阵;S′为待求稀疏向量。 信号的稀疏性,即信号在时域内或者某个特定变换域内使得信号中只有少数的非0元素,剩下的绝大多数元素为0或者很小。 X=ΨS (3) 式中,S中有K(K< 根据本文输出电压信号能量主要集中在低频段的特点,可以采用离散余弦变换(DCT)矩阵和单位矩阵相级联构成的冗余字典进行稀疏表示。假设C是N×N的离散余弦变换矩阵,其矩阵形式为 (4) 然后将离散余弦变换(DCT)矩阵和单位矩阵级联,得到冗余字典:D=[IN,C],式中IN是N×N单位矩阵。另外,经验证,IN和C这两个正交基也满足互不相关性[14]的条件。 通过测量矩阵Φ对N维原始信号X进行观测投影,得到低维度的压缩测量信号Y。测量矩阵Φ通常情况下是一个M×N矩阵,一般需要满足受限等距特性准(Restricted Isometry Property,RIP),也就是存在一个约束等距常数δk∈(0,1),使式(5)对任意K-稀疏信号都成立,其目的是使得到的压缩测量信号Y中的M个值能够有效保留原始信号X中的信息。 (5) 高斯随机矩阵、伯努利随机矩阵等都是传统的测量矩阵,这些矩阵与任意稀疏信号或者稀疏基都保持了很好的不相关性,满足RIP准则。本文用高斯随机矩阵作为测量矩阵。 首先重构算法就是利用测量矩阵Φ和稀疏基Ψ来得到一个压缩测量值YM×1,经该算法后恢复得出原始信号X。具体流程如下:通过式(2)对稀疏向量求解也就是L0范数求解的过程,而对这一范数求解本身就是一个NP难问题,因此在实际模型构建中通常转化为求解L1范数,也就成了一个凸优化问题,其数学模型为 S′=argmin‖S‖1(s.t.Y=ΦΨX) (6) 当前主要采用的重构算法有三类,分别为贪婪算法、凸优化算法和组合算法。其中,贪婪算法运用的最为广泛,常见的有正交匹配追踪算法(OMP)、分段正交匹配追踪算法(StOMP)、正则化正交匹配追踪算法(ROMP)等,但这些算法全部建立在稀疏度K已知的基础上。然而在实际应用中信号的稀疏度K很多都是未知的,因此本文选取正则化自适应匹配追踪算法[15](RAMP)作为重构算法。该方法可在K未知的情况下,通过设置可变步长,逐步估计信号稀疏度,进而实现信号重构。具体算法采用阶段转换逐级增加原子数,并将同一迭代过程细分为多个阶段,利用设置的可变步长替换选中的原子数目,步长和支撑集随之增大,步长逐渐逼近K而重建出原始信号,其中相邻两阶段的支撑集大小的差值即为当前步长。算法具体步骤如下(ε1和ε2分别是控制迭代次数和阶段转换的阈值): ① 初始余量r0=Y,初始步长size≠0,阶段size=1,迭代次数n=1,索引值集合Λ=∅,J=∅; ② 若满足‖r‖2≤ε1,则停止迭代;反之,顺次进入步骤③; ③ 利用相关系数公式μ={μj|μj=|〈r,φj〉|,j=1,2,…,N}计算μ,随后从结果中寻找size个最大值,将其对应的索引值存入集合J中; ④ 将上述集合中的索引值对应原子的相关系数(须满足|μ(i)|≤2|μ(j)|(i,j∈J))正规则化,其结果存入集合J0; ⑤ 更新支撑集ΦΛ,其中Λ=Λ∪J0; ⑦ 若‖rnew-r‖≤ε2,则令stage=stage+1,size=size*stage,转步骤③;否则,令r=rnew,n=n+1,转步骤②。 该模型以带平衡电抗器的24脉波可控电路(导通触发角为0°)为研究对象。在模型搭建时,分别调整整流变压器的额定功率PN=4400 kW,额定交流线电压U2L=1180 V,空载电压U0=1593 V,额定直流电压Ud=1500 V,额定直流电流Id=2933 A[16],并且将负载设置为纯电阻性负载。电路模型如图1所示。 本文构建的24脉波整流电路由4个三相桥电路并联组合而成,其中整流变压器的4组三相副边绕组相位依次相差15°,并且2个12 脉波整流器网侧绕组移相分别为±7.5°,二者之间的导通角相差 15°,这样整个并联电路在工作状态时也就形成了等效 24 脉波整流电路。 图1 带平衡电抗器24脉波可控电路 本文主要研究的是一个或者两个晶闸管发生开路故障的情况,并且将当前的开路故障类型分为以下六类:① 无晶闸管故障;② 1个晶闸管故障(如VT1、VT7等);③ 每个三相桥电路中连接同一桥臂上的2个晶闸管故障(如VT1和VT13,VT9和VT21等);④ 每个三相桥电路中同一半桥的2个晶闸管故障(如VT1和VT9,VT1和VT17等);⑤ 每个三相桥电路中交叉的2个晶闸管故障(如VT1和VT5,VT1和VT21等);⑥ 不同的三相桥电路中的2个晶闸管故障(如VT1和VT3,VT1和VT14等)。最后,选出其中较具代表性和典型性的11种故障类型进行分析。 以VT1和VT13晶闸管发生开路故障为例,其时长为0.02 s,采样频率为50 kHz,数据点N=1000,选择压缩率(M/N)为25%,稀疏度K=50,进行压缩采样和重构实验。通过Matlab2015b进行仿真,其原始电压、重构电压、重构误差的仿真结果如图2所示。 重构信噪比(SNR)为40.23 dB。结合原始信号和重构信号的仿真图像,不难看出,当采样点数分别在200、300和700及800左右时,重构误差显著增大,但其重构精确度依然满足实际需要,体现了该方法的优越性。 不同于传统的故障类型检测方法,提出了基于压缩感知进行故障诊断识别的方法。 ① 通过稀疏、测量和重构原始信号,得到待求稀疏向量S′; ② 由于待求稀疏向量S′保留着原始信号的相应特征和精确地重构出原始信号,对待求稀疏向量S′进行特征参数提取; ③ 将提取到的特征参数作为BP神经网络的输入,最后得到故障的分类结果。 具体流程图如图3所示。 对于待求稀疏向量S′,提取其最大值T1、次大值T2、标准差T3、均方根T4、峭度因子T5和裕度因子T6这六类特征参数。由于特征参数过大,对数据进行以下处理: [T1/T,T2/T,T3/T,T4/T,T5/T,T6/T] 得到的特征参数向量如表1所示。 表1 整流器故障特征向量(导通触发角为0°) 为了对真实情形进行模拟,针对表1中的故障类型,对图1中电路模型参数(如导通触发角)在一个允许的范围内进行变化,得到10种故障信号和正常电压信号各160个样本,每个样本的数据长度均为1000,并且从中随机选取每类样本中的140个作为训练样本,剩下部分作为测试样本,故障分类器采用BP神经网络,具体参数设置中设定训练次数为1000,训练目标误差0.001,隐含层神经元数为10个,输入维数是6维,输出维数是11维,最后分别把VT1开路故障、VT7开路故障、VT1和VT13开路故障、VT9和VT21开路故障、VT1和VT9开路故障、VT1和VT17开路故障、VT1和VT5开路故障、VT1和VT21开路故障、VT1和VT3开路故障、VT1和VT14开路故障和正常信号的训练输出分别设置为(10000000000)T,(01000000000)T,(00100000000)T,(00010000000)T,(00001000000)T,(00000100000)T,(00000010000)T,(00000001000)T,(00000000100)T,(00000000010)T,(00000000001)T。 为了方便分析得出的结果,本文和文献[1]得出的神经网络误差曲线如图4所示。 图4 训练性能对比图 由图4可以看出,本文所用方法得到的神经网络误差曲线其迭代误差在一开始就明显地下降了,在迭代到40次左右时就达到了0.01,最后在迭代了250次之后逐渐收敛于0.001;而文献[1]方法,在迭代了200之后,误差也还没达到0.01,在接下来的迭代过程中误差也没有明显减小,最后在迭代了330次左右时,曲线误差最终收敛于0.001。另外,与文献[1]的故障识别率比较而言,本文的平均故障识别率在97%左右,明显高于文献[1]的故障识别率。总之,本文方法不仅在神经网络训练性能的速度上得到提高,在故障诊断的准确率上也有很大改善。 本文提出了一种利用压缩感知理论来进行24脉波整流器开路故障识别和检测的方法。这一方法首先通过稀疏、测量和重构原始故障信号,得到待求稀疏向量S′;然后利用待求稀疏向量S′进行六种特征向量提取;最后将其作为BP神经网络的输入,最终实现故障分类识别。该方法在特征提取时所用到的待求稀疏向量数据长度只有50,远小于原始信号数据长度1000,在很大程度上减少了特征提取时需要进行处理的数据量。从所选11种故障(包括正常运行状态)诊断的仿真实验中,该方法的故障诊断准确率达到了97%,说明了该方法的可行性,为以后整流器开路故障诊断和识别提供了一定的研究价值。但本文忽略了实际环境中的噪声污染问题,有待进一步研究。1.1 稀疏基设计
1.2 测量矩阵
1.3 重构算法

2 24脉波整流器模型
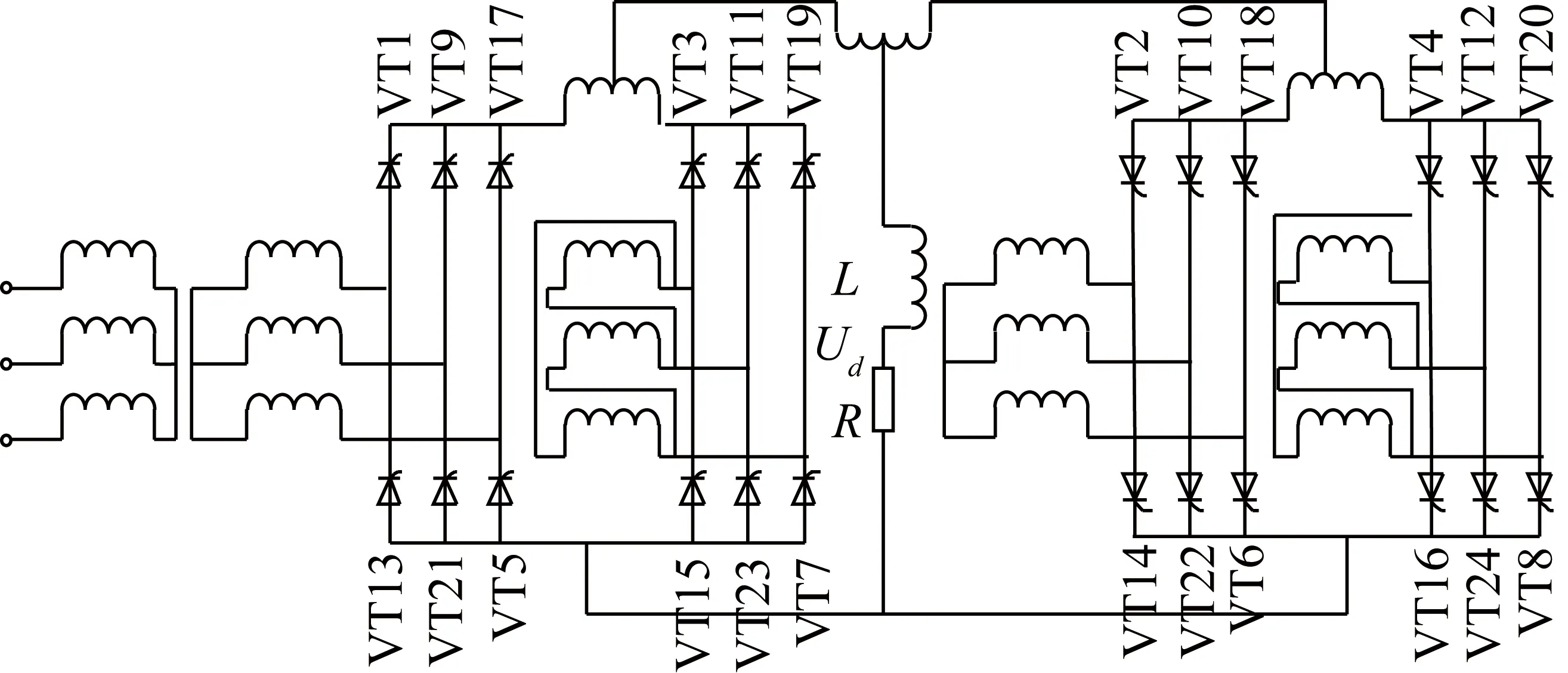
3 压缩感知算例
4 开路故障诊断识别方法
4.1 诊断识别方法原理
4.2 故障特征提取
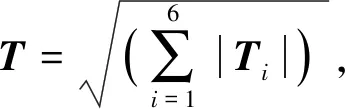

5 仿真实验分析
5.1 仿真参数
5.2 结果分析
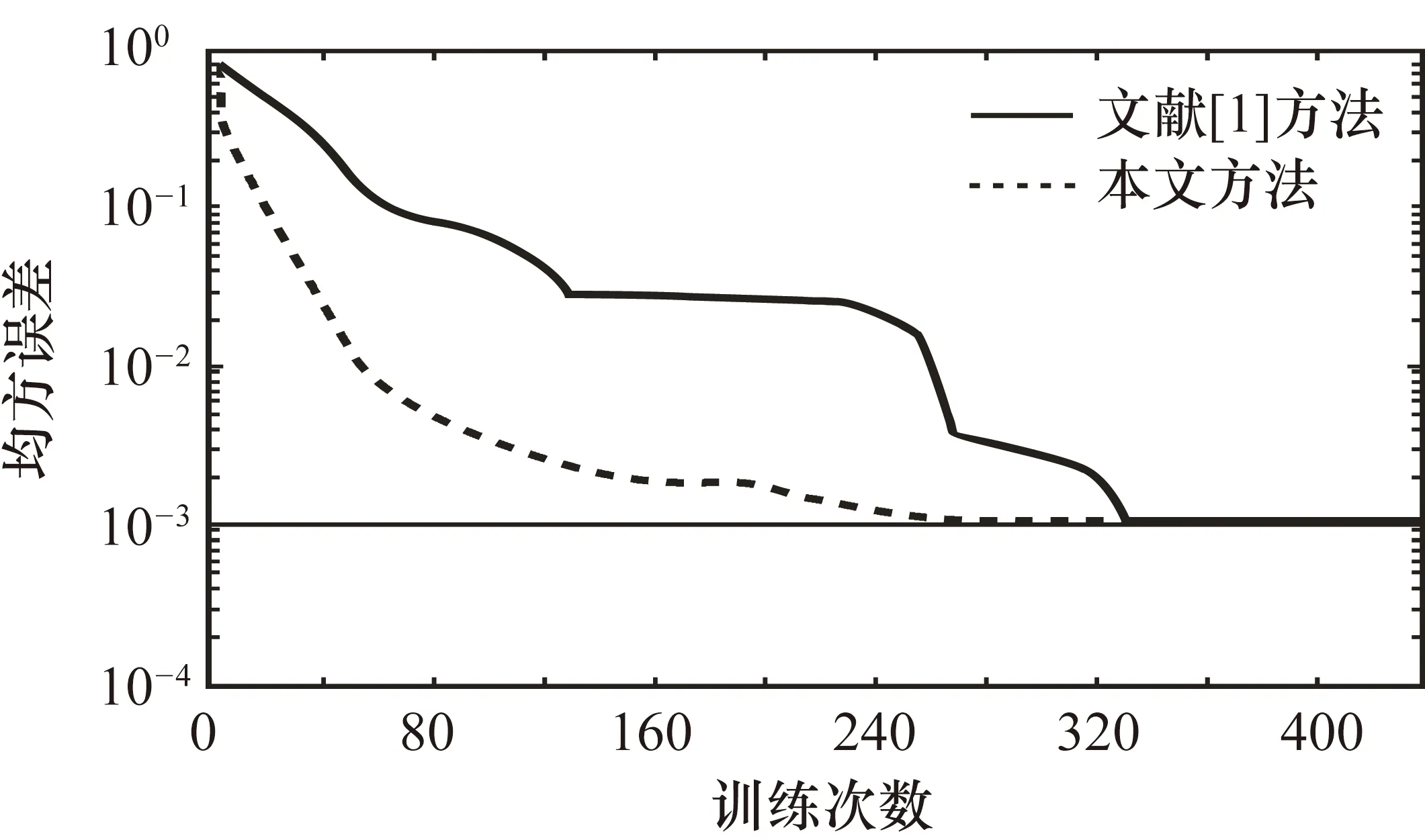
6 结束语

