飞机线缆自动检测系统布局优化设计研究

骆飞平， 韩 冰2， 杨 锋2， 刘泽秋2， 方 强

(1.浙江大学 机械工程学院，浙江 杭州 310027；2.航空工业西安飞机工业(集团)有限责任公司，陕西 西安 710089)

长期以来，传统飞机生产制造缺少自动化生产手段，特别是飞机的检测工艺，严重依赖于工人的手工操作，缺少自动化检测技术，进而导致飞机的检测流程消耗了大量人力及时间成本[1-2]，而整机线缆自动化检测技术的提出可提高飞机生产及检测效率，实现整机线缆导通测试、线束绝缘检查和部分系统阻抗检测工作。

从上世纪60年代起，国外飞机制造行业逐步采用整机线缆自动检测技术。CKT(CK Technologies,Inc.)公司提供的航空线束检测设备服务于空客A320机型整机线缆检测，实现了全机累计超过30000个测试点的自动化检测，其配套提供的测试线缆智能化存储系统、工艺LRU(Line Replaceable Unit)模块、短接终端模块、转接电缆及检测程序可辅助完成整机线缆自动化检测[3]。

国内采用的整机集中式线缆检测技术，将全机测试点统一接入测试系统进行自动测试[4]，但是该技术只适用于某些小型号如ARJ21等机型，若应用于中大型飞机的自动化检测，转接电缆长度及体积过大，不利于使用和存储。

国外采用分段制造、分段检测技术，将23000个测试点分散在部件装配阶段进行测试，仅剩余7000个测试点在飞机总装阶段检测，但该技术并不适应国内飞机的生产现状。

为实现国内大型飞机的自动化检测，引入分布式测试方案。分布式测试箱安置于机舱的检测区需要进行合理的布局规划，该问题可抽象为空间物体的选址问题[5-6]，连接测试箱的控制线布局可抽象为连接路径问题[7-8]。

测试点的分类问题及测试设备定位选址问题均为智能优化问题。智能优化算法可以模拟自然过程，适用性强，多用于解决复杂的工程问题，算法收敛速度快，技术性强，可以用于实现测试系统系统布局的全局优化[9-10]。智能优化算法本质上是启发式优化算法[11]，常见算法有遗传算法[12]、蚁群算法[13]、粒子群优化算法等[14-15]。

本文对系统中各测试方案待改进部分进行数学建模，采用紧邻交换法实现测试点的最优分类，采用连续粒子群优化算法实现整机分布式测试设备的最优选址，采用离散粒子群算法实现测试设备之间的最佳连接路径的选取，实现了飞机线缆自动检测系统布局的轻量化和最优成本设计。

1 分布式测试系统设计及模型建立

1.1 分布式测试系统设计

本系统以国内某大型飞机为研究对象，实现机上电网自动检测的功能。全机测试点达40000多个，其分布情况如图1所示。

根据图1可知，全机测试点分布不均，其中飞机驾驶舱区域和前机身、中机身区域测试点较为密集，飞机两翼与后机身测试点较为分散。若实行飞机线缆检测集中式测试布局方案，即所有的测试点均以中间转接线(以下简称转接电缆)接入到测试系统，会导致测试箱与后机身垂平尾测试区域相连的转接电缆过长，同时，分布在前机身驾驶舱内的测试点与测试箱相连的转接电缆又密，不利于检测系统的正常运行[18]。

图1 某型飞机全机检测点分布

根据飞机的形貌结构和整机测试点分布情况，将测试点划分为9个区域[18]：驾驶舱，舱内，舱前起落架舱，机身整流罩，垂平尾，左机翼，右机翼，左起落架舱，右起落架。

轻量化的测试系统设计引入分布式布局思想，深入研究波音、空客等国际著名航空公司的测试方案，可知分布式测试箱可分担主控的测试工作，从而减少转接电缆的使用。系统应用灵活的分布式架构，在各个测试区域布置分布式测试箱，控制电缆实现了主控单元与分布式测试箱的连接。通过与主控单元级联的方式，测试箱可布置在机舱内部进行测试。

转接电缆用于实现机载电缆插头与分布式测试箱之间的连接，如图2所示。

图2 转接电缆设计示意图

转接线缆由ZIF插头(Zero Insertion Force)、导线束(黑色实线)和插头(A～F插头可与机载电缆相连)组成，导线束从左侧ZIF插头(S点)出发，S～M1段为电缆主干，经M1、M2、M3处进行分叉，称为电缆分支。ZIF插头有150个触点，与测试箱对接，A～F插头与机载电缆对接。每束转接电缆最多可接入150根线束，即A～F插头包含至多150个插针。通过对插头的合理分类，可以有效减少转接电缆的总束数。

分布式测试箱和测试设备之间连接的控制电缆的采购需要进口且造价高昂，未经优化的分布式测试系统需用转接电缆的总长达150 km。为节省设计成本，需优化系统设计，减少测试箱采购数量提高其使用率，减少转接电缆总长。

1.2 插头分类模型建立

如图3所示，以飞机机头最前端O为原点，飞机负航向作为X轴，沿飞机翼展右侧方向为Y轴，高度方向为Z轴，构造一个笛卡尔直角坐标系，简称飞机坐标系。

图3 飞机坐标系

为实现系统轻量化和经济化原则，对机载插头进行合理分类。在满足转接电缆使用少交叉的前提下，利用近邻交换法实现插头自动分类，提高ZIF插头的触点利用率，进而减少转接线缆总长。

以舱内测试区为例，该区域涉及的机载插头数量最多，同时接线关系和连接逻辑也最为复杂。为便于解释问题及数学建模，可将舱内区域看为一个长方体。待测线缆插头悬于机舱内壁，即该长方体的内表面。考虑到舱内层高度较高，将舱内分为上下两层，简称为舱内一层和舱内二层[18]。舱内一层的测试箱布局及其插头分布区域如图4所示。

图4 舱内一层布局

分布式的布局设计可能带来转接线缆对接后的交叉问题。为防止严重交叉，减少各测试箱的重叠区域，将舱内一层测试箱按照左右分开放置，如图4所示，1、3、5、7、9号测试箱分布于测试区左侧，2、4、6、8、10号测试箱分布于测试区右侧。坚持轻量化设计原则，以减少转接电缆交叉使用为基础，实现插头的合理分类，从而减少转接电缆总长。

上述方案以机载插头的实际坐标位置进行分类，可完全避免转接电缆交叉，但也产生了所设计的转接电缆不能充分利用ZIF触点数量的问题。

为减少测试点数浪费，采用近邻交换法，以插头在机上的分布实际情况建立近邻函数。如舱内中插头按照飞机航向X呈两侧排列，此时近邻函数为

(1)

即该区域内插头的排列顺序与x坐标相关，通过y的正负实现舱内左右侧的分离。近邻函数值g(x)相近的插头，可实现交换，并对转接电缆使用的交叉影响较小，通过该方式可提高ZIF触点利用率。

经过近邻函数值计算，提取到n个插头可进行交换，ZIF插头剩余触点数为p。第i个插头gi的插针数量为ωi。每个插头有且仅有一次被选取。求选取插头与ZIF插头相连情况，要求这些插头的插针总数V不大于ZIF插头的剩余触点数，并且其利用率最大化。如图5所示，对所有插头遍历，取第n行中V小于并最接近p的方案。

图5 插头分类

为提高ZIF插头的触点利用率，对部分插头进行适当的交换，本文采用近邻交换的思想进行建模，即按照位置较为接近的插头允许交换的原则进行分组。

为描述n个插头是否被选取，定义决策变量xi：

(2)

设V[i][j]为选取前i个插头，且剩余触点数为j，该情况下ZIF插头的最大插针数，以X=(x1,x2,x3,…,xn)表示插头的选取，此时被选取插头的总针数为

(3)

则ZIF插头的最大利用率数学模型为

(4)

(1) 最优值求取。

① 剩余触点数小于插头的插针数量，则总插针数与第i-1个插头的总插针数相同，即V[i][j]=V[i-1][j]；

② 剩余的触点数可以接纳插头，但是接入之后未必满足到当前的最大利用率，所以在接入和不接入之间择优，即

V[i][j]=max(wi+V[i-1][j-wi],V[i-1][j])

(5)

其中，V[i-1][j]表示不选取第i个插头，wi+V[i-1][j-wi]表示选取第i个插头，则ZIF插头剩余点减少wi。接入插头的最大总针数V[i][j]的数学模型为[1]

(6)

(2) 最优解回溯。

求出局部最优解后，使用最优解回溯法找出最佳组合方案，即求满足该最大利用率的组合方案。

① 若V[i][j]=V[i-1][j]，说明未选取插头i，回溯到V[i-1][j]；

② 若V[i][j]=wi+V[i-1][j-wi]，则选取插头i，且该插头是最优解的一部分，回溯接入该插头前，即V[i-1][j-wi][1]。

1.3 转接电缆长度计算模型

理想情况下，导线的长度为两点之间的直线距离：

(7)

在设计测量时，结合机上的实际使用情况，其中机载插头悬挂于飞机壁板，需考虑导线自重引起的电缆下垂，以及转接电缆存储于移动测试车内，使用过程中需从车框顶部伸出等因素影响，将测试箱与机载插头之间的距离di进行调整：

(8)

式中，k为转接电缆的长度系数；tj为插头j所包含的测试点数；xj-xi表示第i个测试箱与所含插头j之间的X坐标差，yj-yi,zj-zi表示原理相同；hZi为高度补偿系数。为求测试箱最佳的位置坐标(xi,yj,zi)和最短电缆长度di，需要知道该测试箱所含插头的坐标以及测试点数信息，而该信息又受矩阵板卡的分组影响。

矩阵板卡数Mc由近邻交换法实现插头分类后获得，结合测试箱最多可装载7张矩阵板卡这一硬件约束条件，可得该部位的测试箱数量m为

m=ceil(Mc/7)

(9)

式中，ceil()为向上取整函数。

该部位的矩阵板卡分组计算公式如下：

(10)

式中，ai为测试箱i所装载的板卡数。

获取矩阵板卡分组后，该函数可归为非线性连续优化问题求解。

整套系统的转接电缆总长可由式(11)求得：

|zj-(zi+hzi)|-hzi}

(11)

式中，m为系统测试箱数量；n为整机插头数量。

1.4 控制电缆长度计算模型

系统测试设备通过控制电缆进行级联，在设备的连接网络中，设备之间的往返路程不变。针对该问题，引入图论思想，使设备之间的连接网络转化成图论中的加权网络图。而控制电缆的长度最短问题，可以表述成在带非负权值的哈密顿图中寻找一条总权值最小，并且经过所有点且仅一次的回路。

本项目中整套系统包含多条测试支路，而且每条测试支路并不需要形成最后的环路。因此将测试设备之间的级联情况抽象为多支路无返回的变种旅行商 (multiple Traveling Salesman Problem,mTSP)问题[1]：所有控制电缆分成若干支路从同一台主控单元出发，并各自连接相应测试设备后，终止。将分布式测试箱抽象为mTSP的城市，将控制电缆接线关系抽象为路径，以设备的测试点数作为商人在各城市的逗留时间。并且当已知所有测试设备两两之间的距离，以及各个设备上的测试点数目，优化各支路所含测试点数，均衡各支路的分配情况，在保证各个测试箱有且仅有一次接入系统的前提下，获取连接各个支路的控制线缆总长最短方案。

控制电缆将测试设备之间彼此连接，其中设备放置在各层平面，而飞机各区域之间往往因飞机壁板隔离，无法实现直接连接，将两测试单元之间的距离dij调整如下：

(12)

式中，p为控制电缆长度系数，并非定值，视飞机区域而定；xi-xj表示第i和j两个测试箱之间的X坐标差，yi-yj,zi-zj表示原理相同；q为高度差异系数，通过q的选取来对不同层平台上的测试箱进行区分。

按照图论思想，将系统设备之间的连接关系用邻接矩阵表示，定义为

(13)

整套系统的控制电缆总长可由式(14)求得：

(14)

最短路径，即目标函数的最小值fmin。

2 基于粒子群算法的系统布局优化方法

2.1 基于连续粒子群算法的测试箱最优定位

2.1.1 问题描述

以前起落架舱等部分区域为例，总测试点数不超过1050，矩阵板卡数小于7张，只需一个分布式测试箱就可容纳所有插头，将其作为单测试箱区域。

针对单测试箱区域，由于插头位置固定，并且分布式测试箱所接入的测试点也确定，因此，插头的分类问题不会影响测试箱的定位。当该区域的插头分类完成之后，不存在测试箱之间的板卡分组问题，可直接利用连续粒子群算法进行求解。以前起落架舱测试箱定位为例：该区域总测试点数为494点，分配一个分布式测试箱，采用式(15)进行计算：

(15)

式中，n为前起落架舱的插头个数，转接电缆的长度系数取1.2；numi为第i个插头的插针数；xi、yi、zi为插头i的三维坐标；Z0为放置分布式测试箱的平台高度坐标，是已知量；h=1.2 m为移动测试车(用于存储分布式测试箱)的高度。该计算问题的数字化模拟为二维函数，其特征如图6所示，在全局最优值附近函数的梯度较小，使寻常算法难以分辨搜索方向，无法找到全局最优点。该函数为非线性求和函数，并非简单的单调函数，求取过程中，计算量巨大，无法直接通过解析法求得。

2.1.2 粒子群算法实现及测试结果对比

粒子群算法作为一种随机搜索算法，用于多主体优化系统，在不确定型的复杂优化问题中有良好的求解效果。利用连续粒子群算法求取测试箱的最优位置，使转接电缆总长最短。

① 标准(Particle Swarm Optimization,PSO)算法，参数简单可调，收敛速度快，被广泛用于非线性连续优化问题。

② 粒子群算法中引入惯性因子ω，以惯性因子随迭代次数线性递减的方案(Linearly Decreasing Weight,LDW)，可提高粒子群算法的整体性能，具有收敛速度快，靠近目标区域搜索的特性。

③ 本文基于遗传思想对PSO算法进行改进，在PSO算法的迭代中加入遗传机制，考虑到遗传算法后期收敛速度慢的缺点，将总算法的迭代分步执行，第一步以遗传粒子群算法进行初期迭代，第二步利用惯性因子线性下降的粒子群算法，以提高算法的收敛速度。

基于分步遗传思想的粒子群算法，其实现方式如图7所示。

算法关键参数设置：

标准粒子群算法PSO：ω=0.7(多次试验表明，取0.7，效果最佳)；

惯性因子基于迭代次数线性递减的粒子群算法(Linearly Decreasing and Particle Swarm Optimization ,LDPSO)：ω线性递减，ωmax=2，ωmin=0.4；

基于遗传思想的粒子群算法(Genetic Algorithm and Particle Swarm Optimization,GAPSO1)：线性递减，ωmax=2，ωmin=0.4；选择、交叉、变异粒子分别占40%，40%，20%；

考虑到遗传算法后期收敛速度慢的缺点，将总算法的迭代分步执行，第一步以GAPSO1算法进行初期迭代，第二步利用惯性因子线性递减的LDW算法，以提高算法的收敛速度，基于遗传思想的粒子群算法(Genetic Algorithm and Particle Swarm Optimization,GAPSO2)：线性递减，ωmax=2，ωmin=0.4；选择、交叉、变异粒子分别占40%，40%，20%，其中遗传代数占80%，粒子群代数占20%。

算法实现：

分别用上述4种算法，对前起落架舱的分布式测试箱定位函数进行实现，比较测试结果并分析。

其中各算法的循环次数均为50，种群数量设置为3000，各算法的总试验次数为50。目标最优解和目标最优值为算法历次试验求取的最佳一次结果，以及50次试验结果的平均最优值。

表1显示：PSO、LDPSO、GAPSO1、GAPSO2这4种算法都可以求得精度较高的目标最优值以及对应的解。观察表中平均最优值数据，并结合图8(函数的目标最优值)，可以得到前3种算法在这50次试验中，结果存在一定的波动，稳定性较差，并且在最优值精度上也与第4种算法存在差距。图9显示了这4种算法的收敛情况，其中GAPSO2算法具有更早收敛的能力，相对收敛性更佳。基于遗传思想改进的分步GAPSO算法不仅收敛效果好，而且精度高，性能稳定。

表1 4种算法测试结果比较 单位：mm

图8 函数的目标最优值

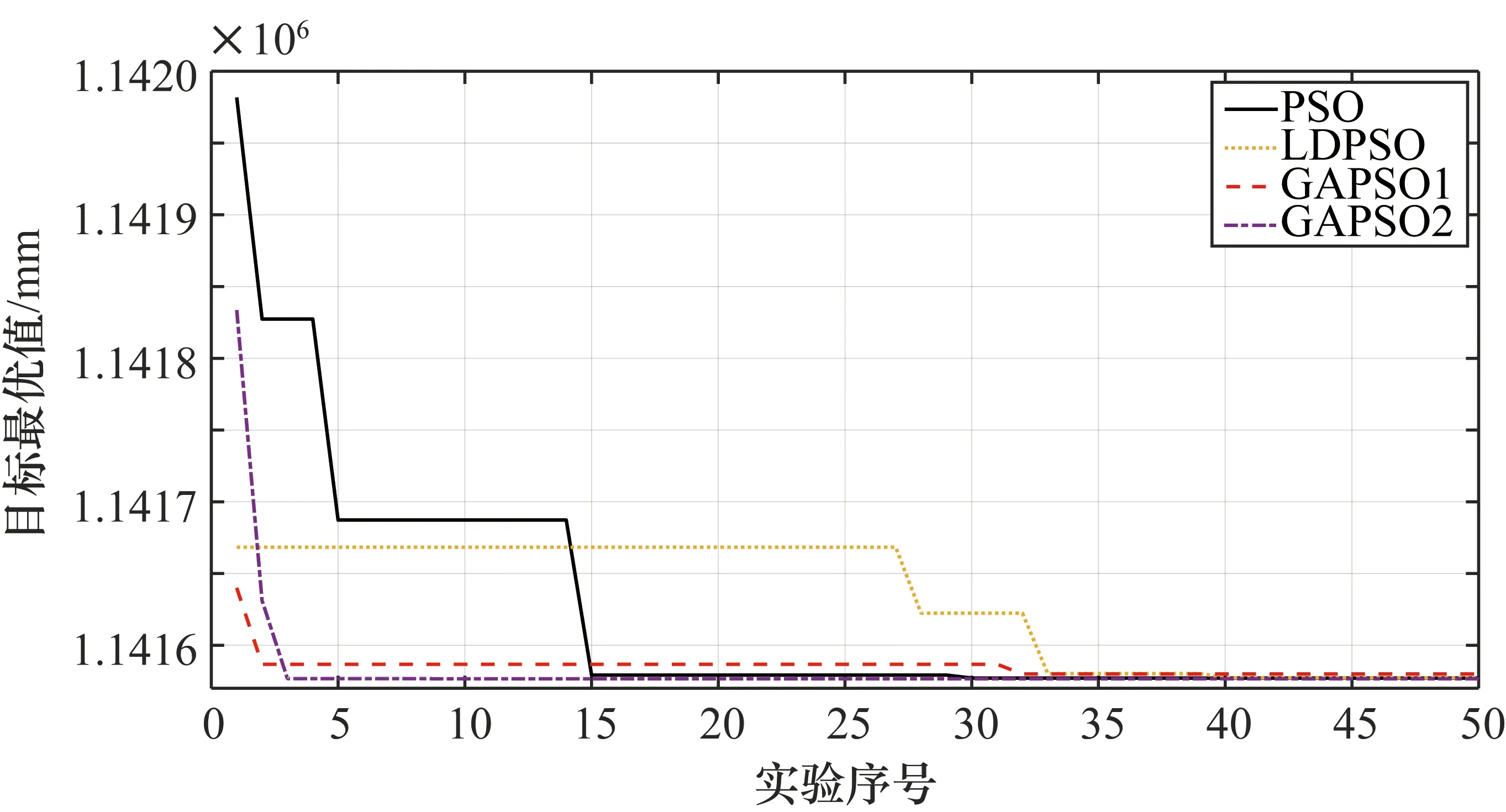
图9 4种算法的收敛情况

结果表明，采用分步遗传粒子群算法，当分布式测试箱的位置坐标为(4471 mm,-614 mm)时，前起落架舱的转接电缆总长最短，为1.142 km。

单个分布式测试箱的价格大约与2.5 km的转接电缆制造成本相当，而前起落架舱转接电缆总长仅需1.142 km，若该区域采用多个分布式测试箱，虽可减少转接电缆长度，但是成本必然更高，因此该区域采用单测试箱测试，也可使分布式测试箱利用率最大化。

2.2 基于离散粒子群算法的测试设备多支路优化

本文将控制电缆连接路径抽象为多支路无返回旅行商问题，将分布式测试箱抽象为mTSP的城市，将控制电缆接线关系抽象为路径，以设备的测试点数作为商人在各城市的逗留时间。并且当已知所有测试设备两两之间的距离，以及各个设备上的测试点数目，优化各支路所含测试点数，均衡各支路的分配情况，在保证各个测试箱有且仅有一次接入系统的前提下，获取连接各个支路的控制线缆总长最短方案。

针对待求解的mTSP这类典型的组合优化问题，本文基于蚁群算法，加入选择、交叉和变异机制，以粒子与个体、种群极值的交叉操作实现对极值编码的跟踪，以粒子的距离函数实现信息素浓度矩阵的更新，从而指导粒子最优路径的生成。

混合离散粒子群算法的原理如图10所示。

图10 混合离散粒子群算法

按照图论思想，将系统设备之间的连接关系用邻接矩阵表示，整套系统的控制电缆总长可由式(14)表示，求取最短路径，即目标函数的最小值fmin。

3 设计结果

3.1 机载插头分类

本套系统基于近邻交换法进行整机插头自动分类，实现轻量化、经济化设计的目标。

如表2所示：表中列出舱内右侧按照X方向进行排序的31个插头坐标，以及插头所包含的插针数。

若插头仅按照坐标X进行分类，则前两条转接电缆的接入测试点分别为128和136，而每条转接电缆最多可以接入150点，该分类方式存在不少空针现象。

近邻交换法步骤如图11所示。

① 按照飞机区域，选定相应的近邻函数；

② 求各个插头的近邻函数值；

③ 针对近邻函数值相近插头，采用近邻交换法实现。

由表2可知，虚线框内表示插头T12～T22的X坐标相同，近邻值相等，可以应用近邻交换法进行操作(这11个插头的X、Y、Z坐标完全相同，可知这些插头属于同一个机载设备，插头之间的彼此交换，不会造成转接电缆交叉)。

表2 舱内右侧部分插头实例

交换规则如下：

① 同一设备上的所有插头可以进行任意交换；

② 同一设备可进行交换的插头不足6个，增加交换代价，即插头最大X坐标差ΔXmax加100；

③ 初始ΔXmax为0，最大ΔXmax为300。

ΔXmax=Xmax-Xmin,0≤ΔXmax≤300

(16)

表2椭圆中各插头近邻函数值相似，属于可交换插头。

除去可交换插头针数，转接电缆实际使用测试点为46。即本案例可简化为针对上述共计11个插头，从中选取出若干插头后，使得所选插针的总和小于并尽可能接近104，以提高ZIF插头触点利用率。

参数设置：

可交换插头数n=11；

剩余可用测试点容量p=104；

可交换插头的插针信息如表3所示。

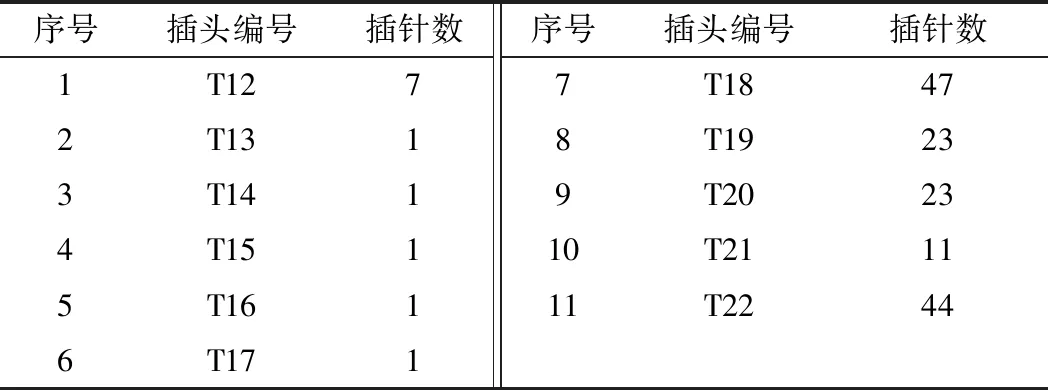
表3 插头信息表

利用最优值求取法分步讨论：

① 当触点剩余容量为1时，如何选取插头，使得ZIF的使用率最大；

② 当触点剩余容量为2时，如何选取插头，使得ZIF的使用率最大；

…

表4中数据表示在给定触点余量和所选插头情况下，插针总数量。

表4 触点余量表

表4中插针总数最大为104，且满足不大于剩余触点p的条件，即104可使ZIF达到最大使用率。

利用最优解回溯求出最佳插头组合：

V[11][104]=V[10][104]

(17)

所以第11个插头未被选取，回溯到V[10][104]:

V[10][104]=V[9][104]

(18)

第10个插头未被选取，回溯到V[9][104]:

V[9][104]≠V[8][104]

(19)

有

V[9][104]=V[8][104-w[9]]+v[9]

(20)

所以第9个插头被选中，回溯到V[8][104-w[9]]，即V[8][81]。直到

V[1][7]=V[0][7-v[1]]+w[1]

(21)

可得最优组合方案为序号1、2、3、4、5、7、8、9，即选取插头为T12、T13、T14、T15、T16、T18、T19、T20时，加入插针总和为104，使得第一条转接电缆触点利用率达到100%。其余转接电缆的交换原理相同，就不再赘述。

分别采用近邻交换法和直接坐标原则，对舱内右侧插头进行分类，分类结果如图12所示。

图12 舱内右侧测试点分类

舱内右侧测试点数总计3778，每张板卡数可接入150针，至少需要板卡26张。由图12可知：按照直接坐标法分类需要板卡29张，而经过近邻交换算法优化后只需26张，板卡利用率100%。

3.2 分布式测试箱定位

分布式测试箱的定位受插头分类影响。多测试箱矩阵板卡的数量与分组最终影响转接电缆的长度。转接电缆的长度计算公式如式(15)所示，但其为非线性求和函数，并非简单的单调函数，无法直接通过解析法求得。而粒子群算法作为一种智能优化算法，求解性能稳定，在不确定型的复杂优化问题中有较好效果。待矩阵板卡分类完成之后，利用分步GAPSO算法求取测试箱的最优位置，使得转接电缆总长最短。

以舱内为例，总板卡数量为49张。由于每个测试箱最多可容纳7张矩阵板卡，因此该区域至少需要7个测试箱。

当该区域采用7个分布式测试箱，结合矩阵板卡数总数为49张，因此每个测试箱内的板卡数均为7张，板卡分组固定。当该区域采用8个分布式测试箱，因矩阵板卡数为49张，存在测试箱内矩阵板卡的分组情况。结合式(9)和式(10)，利用分步遗传粒子群算法，实现对矩阵板卡的分组，同时计算分组下的最佳转接电缆总长。

参数设置：

ω线性递减，ωmax=2,ωmax=0.4；选择、交叉、变异粒子分别占40%，40%，20%，其中遗传代数占80%，粒子群代数占20%。算法的循环次数均为50，种群数量设置为3000。

如图13所示：当测试箱个数为7时，转接电缆总长最短为29.352 km，分布式测试箱内板卡数均为7张。当测试箱个数为8时，转接电缆总长最短为26.723 km，并且此时的板卡分组为舱内左侧测试箱板卡数分别为7、6、5、5；舱内右侧测试箱板卡数分别为7、7、7、5。

图13 转接电缆总长收敛情况

随着分布式测试箱个数的增加，转接电缆的总长度不断减少。其中转接电缆制造成本为a元/米，分布式测试箱价格相当于2.5 km转接电缆造价，为2500a元/个。将测试箱数量不断增加至12个，该区域测试箱个数与转接电缆长度以及总成本如表5所示。

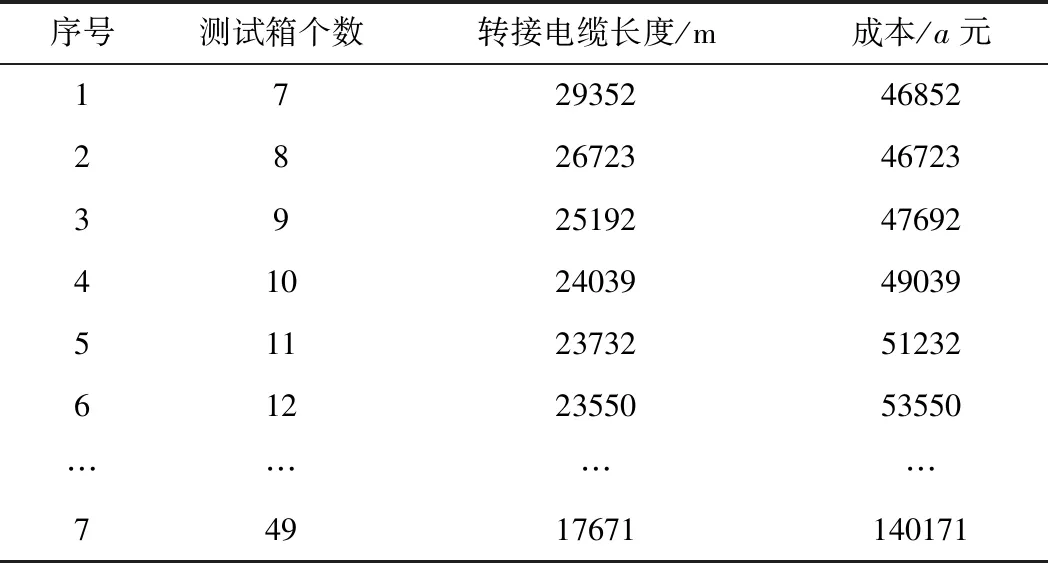
表5 测试箱个数及成本对照表

表5中第7项表示分布式测试箱达最大个数时，即一个分布式测试箱只装载一张矩阵板卡，同样采用分步遗传粒子群算法进行转接电缆总长优化，此时转接电缆总长度为17671 m。

假设分布式测试箱数量为x个，则总成本必满足：

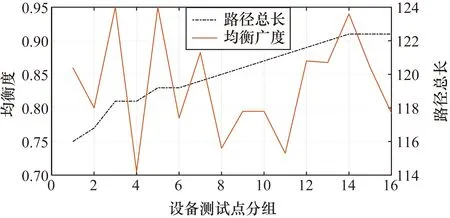
C>2500a×12+17671a, 12

(22)

即当分布式测试箱个数x位于12～49之间，其成本要大于47671a元。

图14 测试箱数量、转接电缆总长及成本曲线

结合图14可知，当分布式测试箱数量为8个，此时的总成本为46723a元，使该区域总成本最低。因此针对舱内区域选用第二种方案，其中分布式测试箱个数为8个，转接电缆总长度为26723 m。

整机各区域的转接电缆长度优化前后如表6所示。

表6 整机转接电缆长度信息

通过对分布式测试箱优化定位，本套测试系统转接电缆总长约为11.9×104m，与按区域直接定位设计结果13.3×104m相比，减少近10%。

3.3 测试设备间连接路径优化

分布式测试箱在连接时，需结合测试现场复杂的作业环境，在整机测试点实现初步的区域分类之后，对各区域局部进行细化分类，包括分布式测试箱的个数，其上矩阵板卡数量(矩阵板卡和转接电缆一一对应，可以视为同一设备)，以及测试单元的摆放位置。

利用设备位置本身处于不同层平台的特性，简化求解问题的规模后，寻找最优路径。为适应该大型飞机总装配生产线的工装布局，将测试单元的控制线路分地面层、舱内层、工装顶层3个部分。并以分布式测试箱较多的舱内层为例，进行具体计算分析。舱内层共计分布式测试箱17个和主控单元1个，其最优位置坐标以及测试点数量如表7所示。

该区域测试点数共计12770，为满足单一支路小于6000点的目标，该区域共采用3支路进行设计。该问题可抽象为mTSP问题，以测试设备为节点，控制电缆的物理连接关系为边，测试点数为权重，构建无向加权网络模型。控制电缆的长度计算公式如下：

(23)

式中，kij为测试箱邻接矩阵(如式(13)所示)；xi-xj表示第i和j两个测试箱之间的X坐标差，yi-yj,zi-zj表示原理相同。

以飞机横向作为分类依据，取近邻函数为：g(y)=y，根据近邻值分类，其中测试单元1、2、8、9作为可调整对象。以支路总长最短，提高各支路均衡度为目标，利用混合离散粒子群算法进行优化处理。

参数设置：

信息素浓度参数为1，信息素启发因子为5，Rho信息素挥发因子为0.1，信息素增强系数为100。

计算各组对应的均衡度和最短路径总长的试验结果如表8所示。

均衡度与最佳路径的关系如图15所示。

本文以均衡度大于0.9，路径总长最短为原则，选择第16组，该组均衡度为0.9132，各组的测试点分别为4747，4168，3855，最佳路径总长为117.7 m。

图15 均衡度及其最佳路径(其中均衡度按照由小到大排序)

飞机地面层测试点分组均衡度为0.96，各组测试点分别为2939和2686，最佳路径总长为92.8 m；工装顶层测试点分组均衡度为0.91，各组测试点分别为4055，3288，4037，路径总长为93.7 m。

货舱层的实际控制线路如图16所示(图17、图18为地面层与工装顶层的控制线路)。

通过计算优化，本套测试系统共提供8条支路，每条支路最大测试点数不超过6000，各支路控制电缆级联长度均小于100 m。系统优化后控制电缆总长为304.2 m，原设计结果为371.0 m，减少18%。

图16 货舱层控制支路

图17 地面层控制支路

图18工装顶层控制支路

4 结论

① 利用近邻交换法实现机载插头的自动分类，并借鉴0-1背包问题，将矩阵板卡的利用率从89.7%提高至100%；

② 为实现转接电缆总长最短，取测试箱内待连接点数量以及测试箱空间位置坐标建立优化模型，再通过对多种智能优化算法原理分析，选用标准粒子群算法，惯性因子线性递减粒子群算法，基于遗传思想的粒子群算法以及为提高算法后期收敛速度的分步遗传粒子群算法，对分布式测试箱可接入点数和测试箱位置进行优化，减少转接电缆总长近10%；

③ 将控制电缆连接路径抽象为多支路无返回旅行商问题，取测试箱的空间位置为节点，测试箱之间的控制线缆为边，测试箱内的对接点数量为权重，构建无向加权网络模型。针对传统离散粒子群算法在解决多支路无返回的变种旅行商问题时易早熟等缺陷，基于蚁群算法，引入遗传选择、交叉和变异思想，利用后代粒子与个体、种群极值的交叉操作来跟踪极值编码，利用粒子间的距离函数来更新信息素浓度矩阵，并以支路总长最短、支路均衡为目标，实现测试系统多支路优化设计，减少控制电缆总长18%。