基于时间同步的船体姿态基准传递技术

杜红松，于东康，尹洪亮，杨 洺，郝 强

(1.海军研究院，北京 100073；2.中国舰船研究院，北京 100192；3.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨， 150001)

0 引 言

姿态基准传递技术通过准确测量船体局部点位与基准惯导所在点位之间的变形角，使船载系统（如雷达系统、武器发射系统及导航系统等）工作在统一的坐标基准之下，从而保证各系统的协同工作。在诸多姿态基准传递方法中，基于惯性量匹配的方法凭借其测量精度高、受环境影响小等优势，已成为广受研究的主流方法[1-4]。惯性量匹配法的原理是利用主惯导和待测点位捷联惯导的惯性量输出建立匹配关系、借助Kalman滤波实现对船体变形角的估计，保证其估计精度的前提之一是确保2组惯性量之间严格的数据同步。为解决数据同步问题，文献[5]与文献[6]分别研究了时间延迟对于角速度匹配算法与惯性姿态匹配算法的精度影响，并设计了时延在线估计补偿算法，但均未考虑从采集方式上解决时延问题；文献[7]提出通过时钟同步解决数据同步采集问题的方案，但缺少对变形角测量结果的试验验证。

本文在角速度匹配算法的基础上，首先通过仿真对时延误差的影响进行研究。为消除时延对姿态基准传递过程的影响，一方面提出基于晶振校正的时间同步采集方案，以实现从采集机制上控制时延，同时设计了引入时延的扩维Kalman滤波器，进一步从算法角度完成对时延误差的补偿，达到高精度测量船体变形角的目的。通过仿真试验，验证了所提基于时间同步的船体姿态基准传递方案的准确性与可靠性，对于该领域的研究具有一定的参考价值。

1 角速度匹配算法

1.1 角速度匹配原理

基于角速度匹配的船体姿态基准传递方法利用2套光纤陀螺捷连惯导INS1和INS2，它们的安装位置及坐标定义如图1所示。其中，INS1作为船体主惯导，提供全船设备的姿态基准信息，定义其坐标系为。INS2安装于待测位置，定义其坐标系为，INS1与INS2大致对准，但由于船体变形角的存在，、之间存在一个小角度偏差。

图1 两套惯导系统安装示意图Fig.1 Two sets of inertial navigation system installation diagram

图2 变形角示意图Fig.2 Diagram of deformation angle

其中，

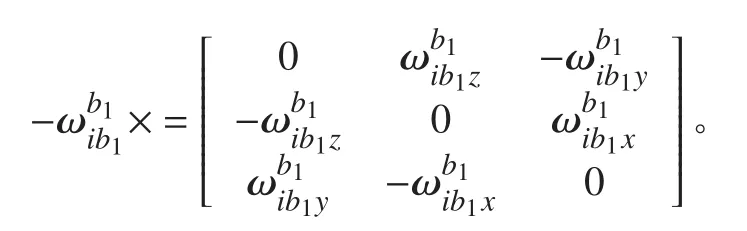
由角速度匹配方程式（4）可知，角速度差值与总变形角、动态变形角速度之间存在线性关系，在此基础上合理设计Kalman滤波器，可实现对变形角的最优估计，实现船体姿态基准的传递。

1.2 卡尔曼滤波方程

在建立Kalman滤波方程之前，首先对静态变形角、动态变形角进行建模。在本文研究中，将静态变形角建模为短时间内的常值模型，即有；对于动态变形角，建模为白噪声驱动的二阶Markov过程，其滤波器方程可表示为：

对角速度匹配方程做进一步整理，在式（4）基础上，考虑光纤陀螺漂移影响，得到：

进一步写出系统状态方程：

其中：

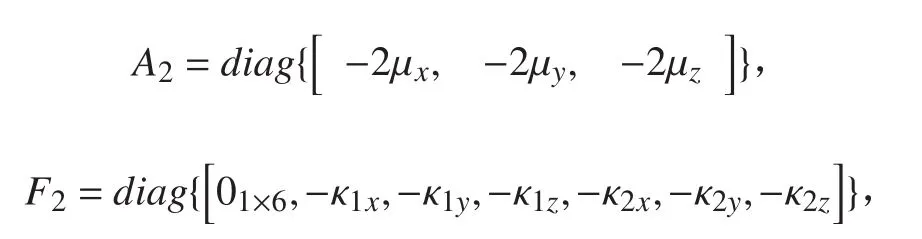
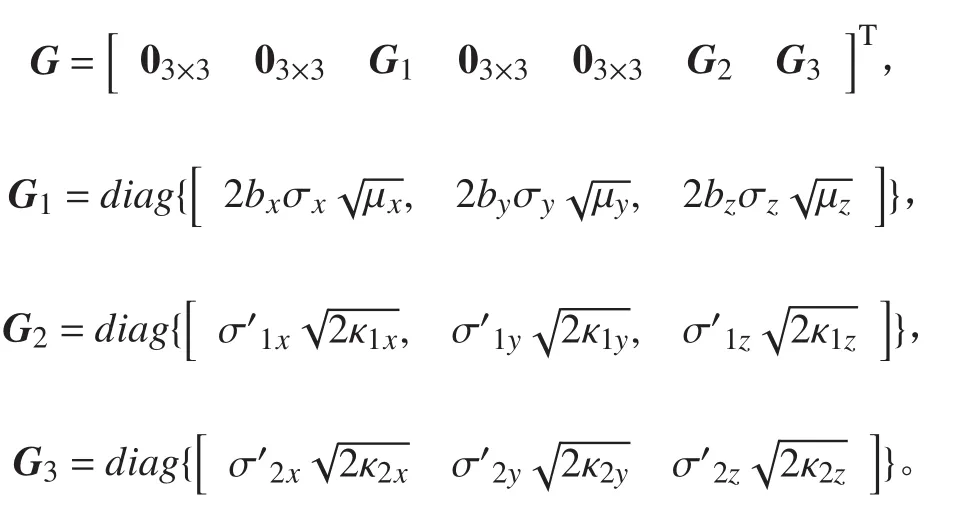
系统量测方程为：

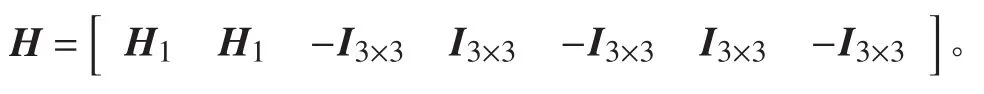
2 时间同步方法设计

2.1 时延产生的原因

对于实际测量条件来说，由于2套系统信息采集与信息输出时间的差异，将会导致二者数据存在延迟。如果时间延迟量过大，将给测量值引入较大的误差，影响算法的收敛速度，并最终导致船体变形角估计值的准确性严重降低，无法完成姿态基准的精确传递。

时延产生的原因可以归结为两点：一是由于2套惯导系统内部晶振不同步，导致数据采集过程存在延时，该延时量大概在40～120 ms之间；二是由于当2套惯导系统相隔较大距离，且传输线路的材质密度不同时，会使得信息传输速度存在差异从而导致信息传输过程存在延时。

2.2 基于晶振校正的同步采集

经2.1节分析，导致时延的很大方面原因在于2套系统的晶振不同步，因此直接采集的2组数据将存在时延偏差。为从采集机制设计上解决时延问题，本论文设计基于晶振校正的同步采集方案，即将GPS的1PPS作为外部基准源，利用1PPS信号驯服2套惯导系统的晶振[9-10]。

由于GPS提供的1PPS信号具有很高的精度，一般接收机输出的1PPS信号的上升沿与UTC的统计误差精度为1 μm，并且不存在累计误差，所以可用1PPS信号对2套系统陀螺晶振进行驯服校正，从而保证2套系统的时钟同步。另外，惯导系统在接收到1PPS信号的同时也接收UTC时间信息，可以为惯导数据添加时间标记，即“打时戳”，便于在数据同步采集单元内部进行时间取齐，同步采集方案如图3所示。

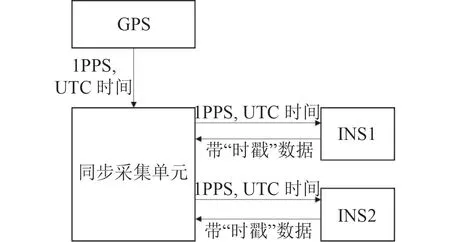
图3 基于晶振校正的同步采集方案图Fig.3 Synchronous acquisition scheme diagram based on crystal oscillator correction

基于上述同步采集原理，理论上能将时延量控制在10 ms以内。但仅靠该方法无法彻底解决时延影响，还需从算法角度对残余时延误差进行补偿。

2.3 引入时延量的扩维滤波器

1.2节对于Kalman滤波器的设计中未考虑2组陀螺的数据延迟，在此条件下，将角速度匹配方程重写为：

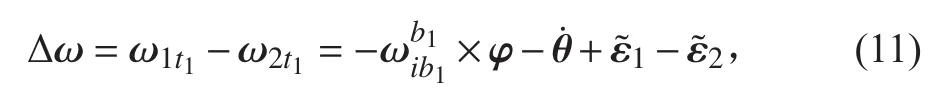
将式（12）代入式（11）中，得到考虑时延之后的角速度匹配方程：

其中，

3 仿真试验与分析

为验证本文所提基于时间同步算法的姿态基准传递方法的有效性，设置仿真试验。仿真中假设船体在系统时处于摇摆状态，分别绕纵摇轴、横摇轴和方位轴以正弦形式进行三轴模拟运动；2套惯导系统陀螺精度分别为0.01°/h和0.05°/h；假设经数据同步采集之后，残余时延长度分别为10 ms（理想情况）与40 ms（非理想情况），对2种情况船体变形角度进行仿真解算，仿真时间为10 min，得到结果如图4～图9所示。

图4 10 ms时延情况静态变形角估计曲线Fig.4 Static deformation Angle estimation curve for 10 ms time delay

图5 10 ms时延情况动态变形角估计曲线Fig.5 Dynamic deformation angle estimation curve for 10 ms time delay

图6 40 ms时延情况静态变形角估计曲线Fig.6 Static deformation angle estimation curve for 40 ms time delay

整理后的估计误差见表1，分析图表结果可得出结论：引入时延的扩维滤波器能够准确估计出时延量，时延补偿后的估计曲线可以较好地跟随真实值的变化，且10 ms时延情况下的解算情况优于40 ms情况。由表1可知，时延补偿算法能够达到10 ms左右的估计精度，较未补偿情况提升明显。另外，鉴于时延增大时算法的估计精度有所下降，若配合本文所提基于晶振校正的时间同步采集方案将时延量控制在10 ms以内，再结合时延补偿算法进行变形角估计，理论上可得到较为理想的解算精度，从而实现高精度的船体姿态基准传递。

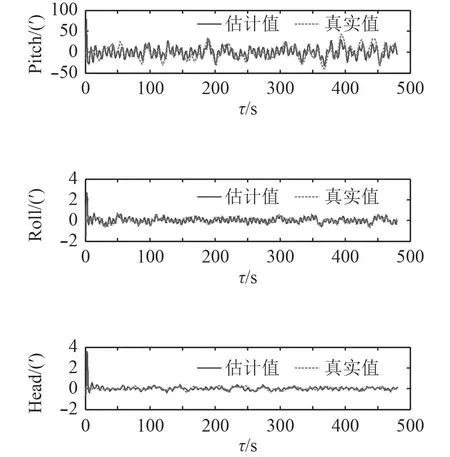
图7 40 ms时延情况动态变形角估计曲线Fig.7 Dynamic deformation angle estimation curve for 40 ms time delay

图8 10 ms时延情况时延量估计Fig.8 Time delay estimation for 10 ms time delay

图9 40 ms时延情况时延量估计Fig.9 Time delay estimation for 40 ms time delay

表1 变形角测量结果统计表Tab.1 Statistical table of deformation angle measurement results

4 结 语

本文研究基于角速度匹配算法的船体高精度姿态基准传递技术，并重点针对其中2套惯导系统数据同步问题开展方案设计，从2个角度入手解决时延问题：一是从数据采集机制上，利用GPS提供的1PPS作为高精度基准时钟源，设计基于晶振校正的同步采集方案；二是从算法设计上，研究引入时延量的扩维Kalman滤波算法，通过2种方法相结合以实现对时延偏差的控制与补偿，从而准确解算出船体变形角，达到船体姿态基准高精度传递的目的。

从仿真试验结果来看，本文所提基于时间同步的姿态基准传递方案，能够将测量误差控制在10′左右，具有一定的工程价值。下一步工作应针对该方案在实船环境下的解算效果做进一步研究。