内爆下爆距对舱壁变形挠度影响的数值模拟研究
赵鹏铎,黄 松,,尹建平,李旭东,,徐豫新
(1.海军研究院,北京 100161;2.中北大学 机电工程学院,山西 太原 030051;3.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
0 引 言
反舰导弹对大型水面舰船尤其是舷侧结构危害巨大,其击中目标后能够穿透外板进入舱内爆炸,对舰艇内部重要舱室形成严重威胁。舱室内部爆炸与开放空间相比差异较大,约束的空间环境对爆炸的毁伤效果甚为明显,引起了国内外学者的关注。Zyskowski等[1]开展了系列小当量TNT舱室内爆炸试验与数值计算研究。C.Geretto等[2]分别在空爆、半密闭舱室和全密闭舱室3种情况下进行了低碳钢板在爆炸载荷下的响应研究。侯海量等[3-4]通过数值仿真和实验研究了舱内爆炸下的冲击载荷特性及其作用过程,总结并提出了内爆载荷下舱室板架结构的4种失效模式。孔祥韶[5]通过数值仿真研究了舱内爆炸载荷的准静态特性并给出载荷简化的计算方法。陈攀等[6]采用数值模拟方法研究了舱室内爆冲击波壁面反射特性及爆点位置对舱室内爆载荷的影响。熊飞等[7]通过数值模拟详细分析了舱室内爆毁伤全过程,并研究了炸点位置对舱室内爆毁伤效应的影响。可以看到学者对舱内爆炸问题进行了大量的研究,但多数研究是将爆源置于舱室中心,对内爆问题进行了简化,实际情况中爆源在舱内的位置具有一定随机性。也有部分学者研究了爆源位置对内爆效果影响,但也仅以整个舱室为对象进行了破坏分析,未针对单个舱壁的变形情况进行研究。在之前的某内爆实验中发现改变爆源位置后,远爆端和近爆端舱壁的挠度变化规律与空爆下有所差别,为研究内爆下爆点位置对舱壁变形的影响,本文使用有限元软件Autodyn建立了舱内爆炸的有限元模型,对比实验验证了数值仿真的可靠性,通过改变舱内爆源位置研究了远爆端和近爆端舱壁的变形挠度,针对某一工况分析了舱内载荷的变化过程,结果可为舱壁的防护研究提供一定的参考。
1 数值计算方法的验证
孔祥韶[5]采用实验的方法测试了舱壁有开孔的舱室模型内爆炸冲击波的压力,实验模型整体尺寸为1.8 m×0.8 m×0.8 m。实验模型、模型尺寸及测点布置如图1所示。本节取实验4种工况中的工况1建立有限元模型进行数值仿真,其开孔半径为50 mm,55 gTNT位于舱室中心处爆炸,通过仿真结果和实验结果对比,验证仿真方法的可靠性。
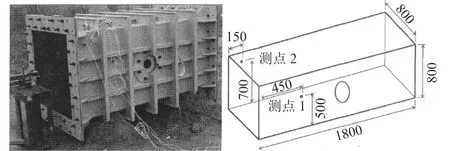
图1 实验模型及测点布置[5]Fig.1 Experimental model and measurement point arrangement
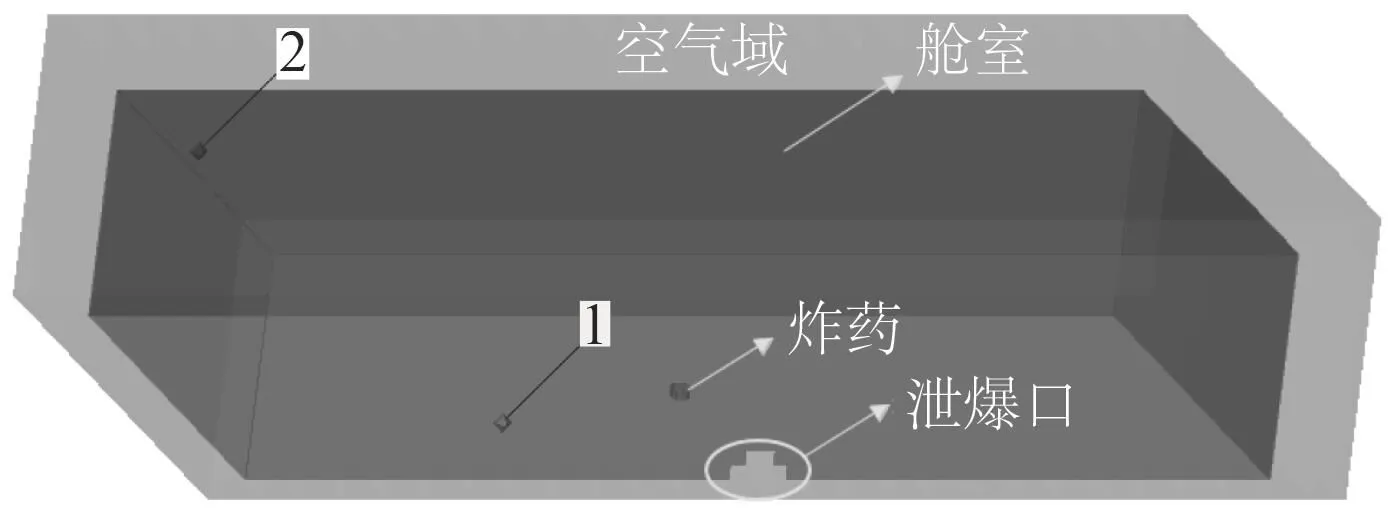
图2 1/2有限元模型Fig.2 1/2 Finite element model
考虑到模型具有一定的对称性,为简化计算和节省时间,采用1/2模型进行仿真计算。舱室有限元模型由空气域、舱壁和炸药组成,如图2所示。由于舱壁的厚度远小于舱室的整体尺寸,在建立舱壁时采用壳单元建模,并赋予相应的厚度值,然后添加刚性边界条件使其为刚性舱壁,模拟舱室模型主体结构。除对称面外,在空气域的四周添加“Flow-out”流出边界条件。根据实验中传感器的布置位置,在仿真模型中相同位置添加高斯点,以得到该位置的压力时程曲线。
数值仿真中空气采用理想气体状态方程,状态方程表述如下:

式中:γ为空气的比热;ρ为空气密度;e为空气内能。本文取γ=1.4,ρ=1.225×10-3g·cm-3,e=2.068×103kJ/kg。
炸药采用TNT装药,用JWL状态方程描述,它本质是一个经验公式,其数据来源于一系列的物理实验,能很好地反映产物的体积、压力和能量特性,适用于大多数的高能炸药。爆轰产物的气体压强公式由下式给出:
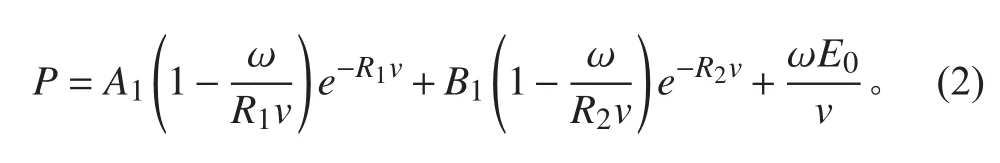
式中:A1,B1,R1,R2,ω为实验拟合参数;E0为单位体积爆轰产物的内能,v为爆轰产物相对比容,其中v=ρ0/ρ,ρ0为炸药初始密度,ρ为爆轰后某一时刻密度。TNT参数采用Autodyn材料库中的默认参数[8]。
舱壁材料采用Q235钢,其用Linear状态方程和Cowper-Symonds强度模型来描述,在AUTODYN中对应参数如表1和表2所示[4]。
通过模型中施加的高斯点提取两测点的压力时程曲线,如图3和图4所示。仿真计算结果与实验结果对比,如表3所示。测点1和测点2的仿真结果和实验结果的误差分别为4.2%和18.4%,可见仿真方法具有一定的可靠性。

表1 Q235钢Linear状态方程参数Tab.1 Q235 steel parameters of Linear EOS

表2 Cowper-Symonds强度模型参数Tab.2 Q235 steel parameters of Cowper-Symonds
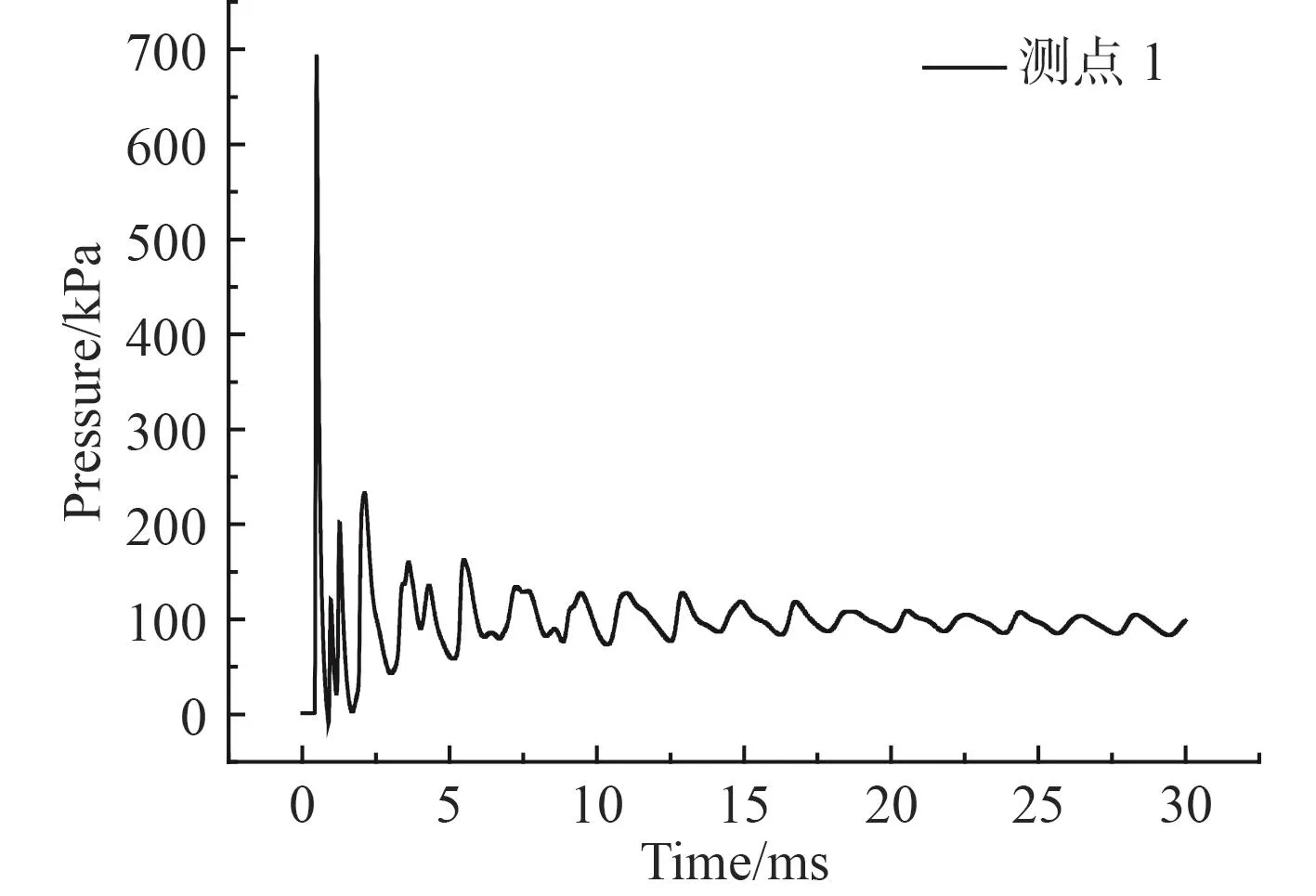
图3 测点1处压力时程曲线Fig.3 Pressure temporal curves of point 1
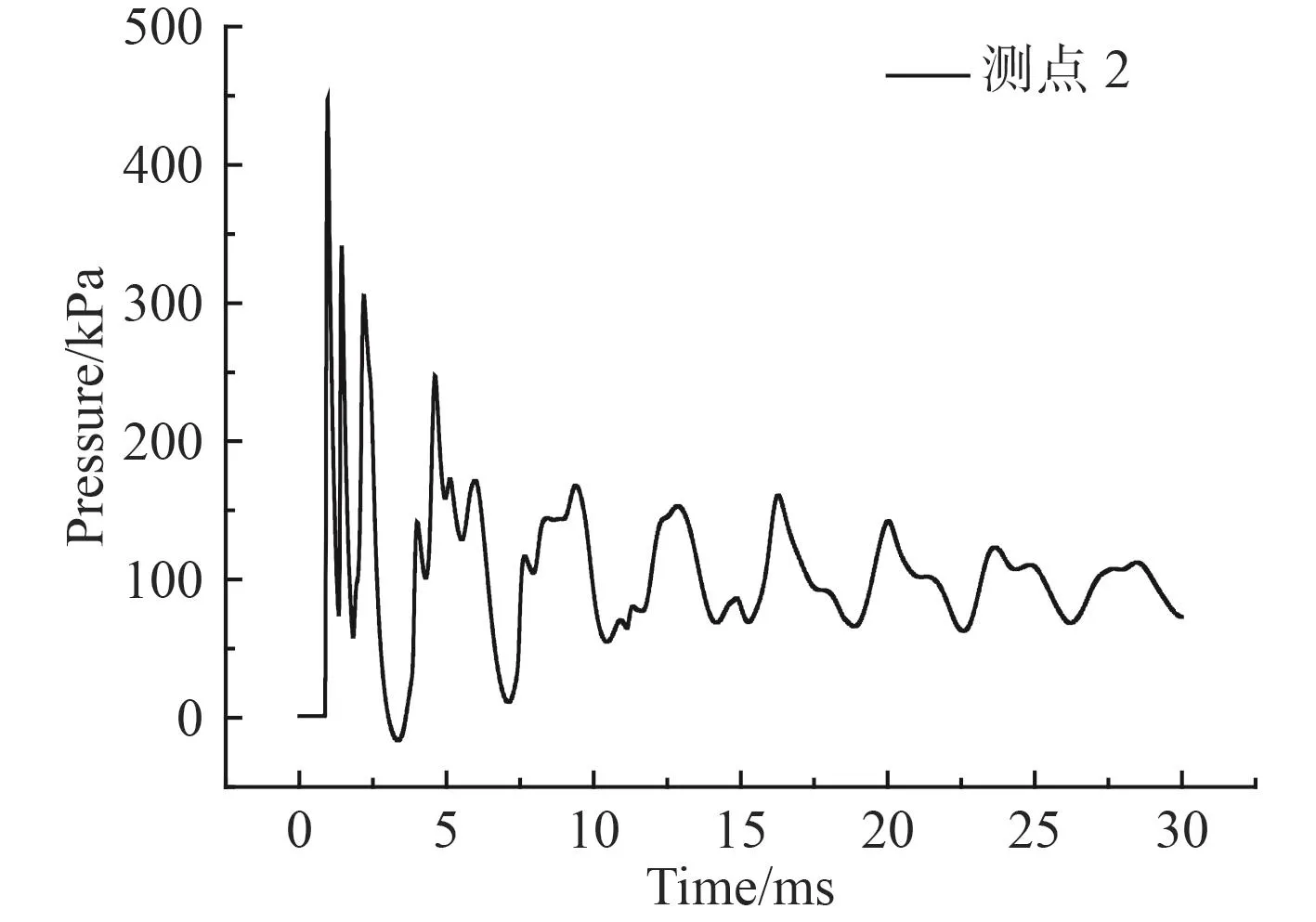
图4 测点2处压力时程曲线Fig.4 Pressure temporal curves of point 2

表3 仿真结果与实验结果对比Tab.3 The calculation is compared with the experimental results
2 内爆下爆距对横舱壁变形的影响
实际情况中导弹穿舱爆炸时,爆源在舱内的位置具有一定随机性,相对于某舱壁目标来说爆源位置的不同导致爆距不同,对舱室的毁伤效果不同。本文在研究不同爆距下,舱室舱壁变形破坏情况时,为简化研究内容,在建立舱室模型时将舱室的纵舱壁设置为刚性体,通过改变爆源相对于舱室两端横舱壁的位置来达到改变爆距的目的。
2.1 模型的建立及工况设计
采用上节仿真模型的建模方法建立1/2舱室模型。舱室的整体尺寸为1.0 m×0.5 m×0.5 m。在舱室的纵舱壁上添加刚性边界条件,模拟舱室的主体结构,左、右横舱壁为厚度为1.8 mm的正常舱壁,材料失效参数为0.2[9]。在左、右横舱壁几何中心处施加高斯点以获取两舱壁的位移时程曲线,并在舱内两舱壁附近的空气域施加高斯点以获取该处的压力时程曲线。TNT药量为13.5 g,爆源位置设计为5个位置,分别对应5种工况,位置1爆源位于舱室的几何中心,位置2~位置5依次靠近右横舱壁,每个位置间距100 mm,具体工况内容如表4所示。
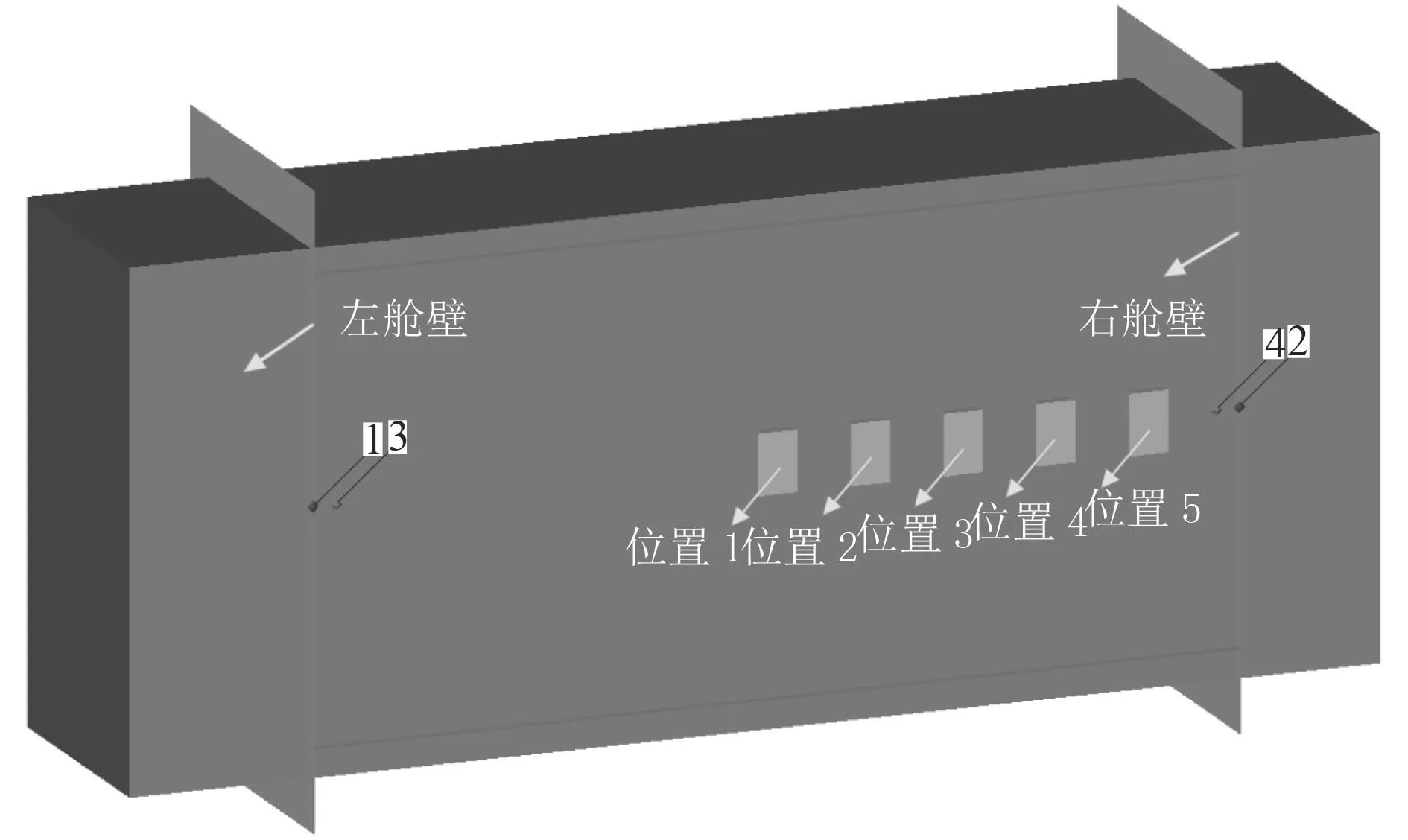
图5 1/2有限元模型Fig.5 1/2 Finite element model
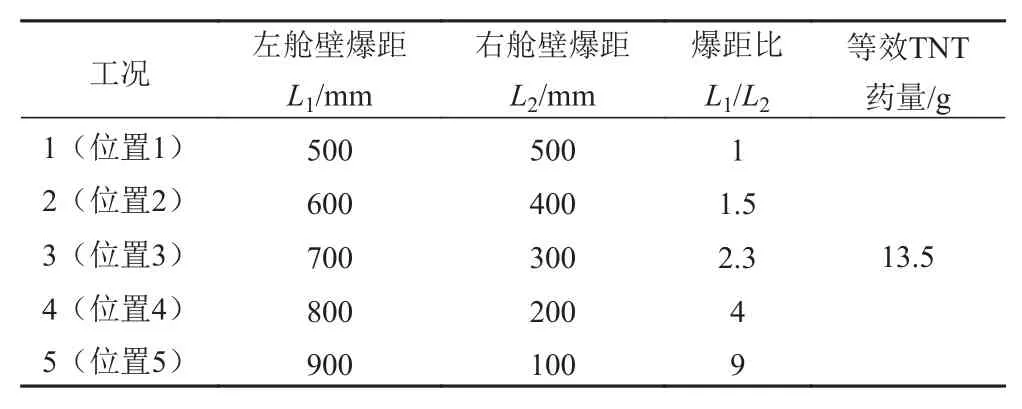
表4 详细工况表Tab.4 Detail working condition
2.2 舱壁挠度变化分析
通过对以上5种工况进行仿真分析,得到了不同工况下左右横舱壁的变形情况,可以看到舱壁均未发生破口,具体情况如表5所示。左、右舱壁的挠度变化曲线如图6和图7所示。对比工况2~工况4,可以发现远端左侧舱壁的变形挠度总大于近端右侧舱壁变形挠度,且随L1/L2的增大,两舱壁的挠度差也逐渐增大。从表5可以看到,左侧舱壁的变形挠度随着L1/L2的增大而增大,与自由场爆炸时爆距越大,压力越小,靶板的变形挠度越小的情况相反。从图6的变化曲线可以看出,随着爆距L1的均匀增加,舱壁变形挠度量也呈线性增加,在本文的舱室模型工况中,爆距每增加100 mm,左舱壁变形挠度约增加11 mm,为爆距增量的11%;而右侧舱壁随着L1/L2的增大,变形挠度呈减小趋势,从工况2~工况4可以看到,右侧舱壁的变形挠度虽有下降,但变化不大。在爆距L2为100 mm时(工况5),右侧舱壁的变形挠度出现增大。从图7可以看到,工况5的右侧舱壁挠度变化曲线与其他工况不同的是在达到最大变形挠度前出现多次波折,在0~0.7 ms间与挠度变化速率较大,在0.7~0.92 ms挠度出现降低,这是因为工况5的右侧舱壁距爆源近,炸药爆炸后在爆轰产物膨胀过程中,在紧靠右侧舱壁内部一定区域出现负压区,在舱壁内外压力的作用下,舱壁变形出现回弹[10]。随后爆轰作用继续进行导致右侧舱壁内部压力上升,大于舱外压力,舱壁的变形挠度继续增大,直到达到最大变形挠度。

表5 不同工况下左右横舱壁变形情况Tab.5 Deformation of left and right transverse bulkhead under different working conditions
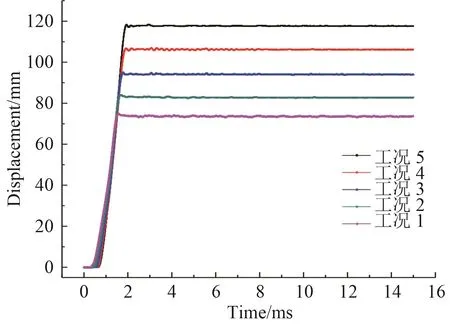
图6 左横舱壁挠度变化Fig.6 Deflection changes of left transverse bulkhead
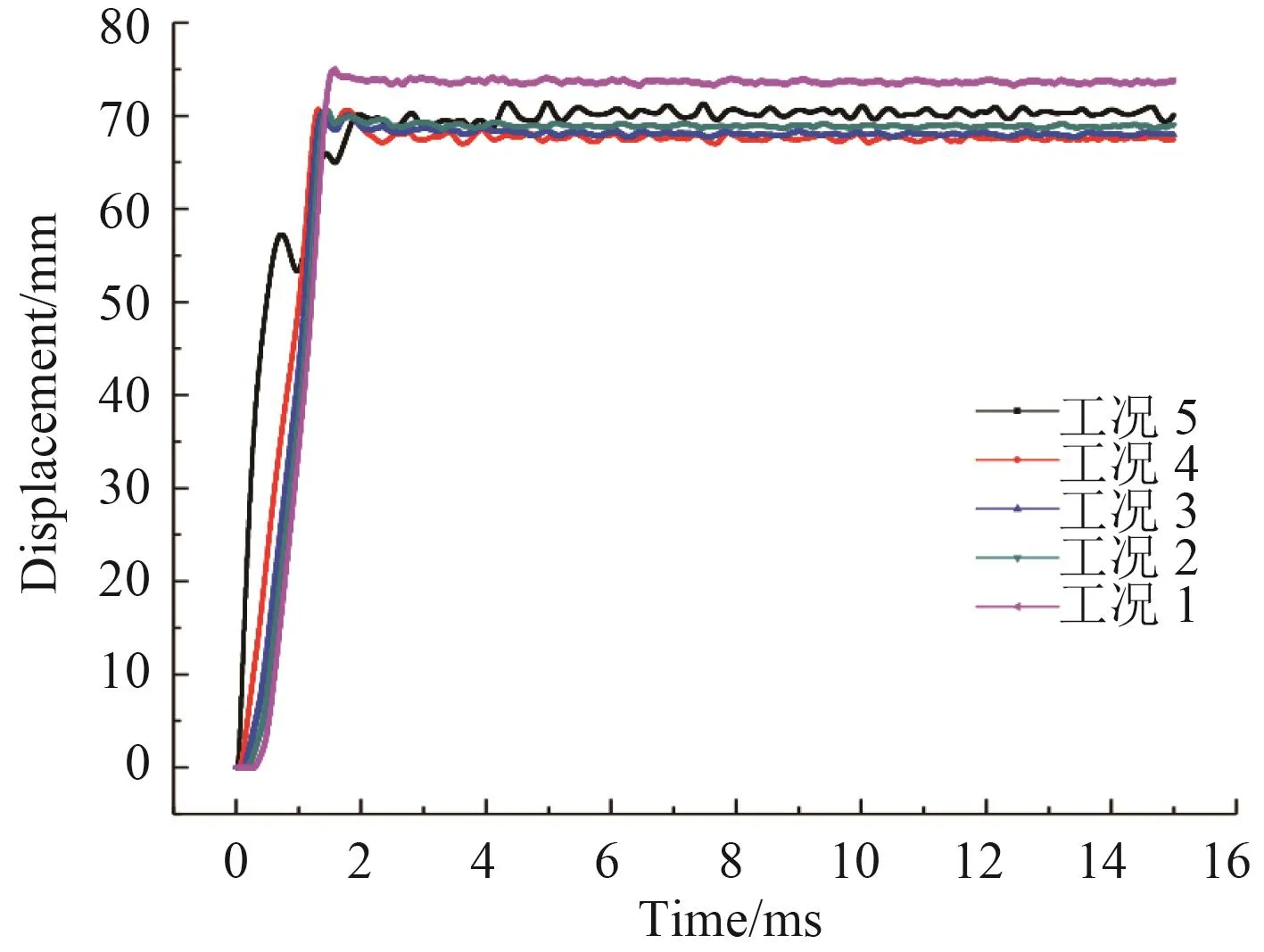
图7 右横舱壁挠度变化Fig.7 Deflection changes of right transverse bulkhead
3 舱内压力变化分析
针对舱室内爆仿真模型中出现的远端左侧舱壁变形挠度大于近端右侧舱壁变形挠度这一现象,以典型工况2为例,分析左右舱壁附近舱内压力及冲量的变化情况。由于右侧舱壁靠近爆源,炸药爆炸后初始冲击波先到达右侧舱壁,从图8可以看到右侧舱壁测点处初始冲击波超压为6.30×103kPa,随着爆轰的进行,在0.68 ms时,左侧舱壁测点处的冲击波压力峰值为1.02×104kPa,约为右侧舱壁测点处压力的1.62倍。从表6中可以看到爆炸冲击波在向爆距较远的左侧舱壁传播的过程中,来自右侧舱壁及四周刚性舱壁的反射冲击波在舱室中轴线区域发生汇聚形成高压区(见0.35 ms时刻),形成的高压区向左侧移动的过程中与向左传播的初始冲击波发生叠加并同时作用于左侧舱壁上(见0.45~0.70 ms时刻),所以首次到达左侧舱壁的冲击波并不单是初始冲击波,而是初始冲击波与舱内反射冲击波作用的叠加波,故压力峰值大于右侧舱壁处的压力。随后冲击波在舱内发生复杂的反射和叠加,最终在舱内形成作用时间很长的准静态压力。
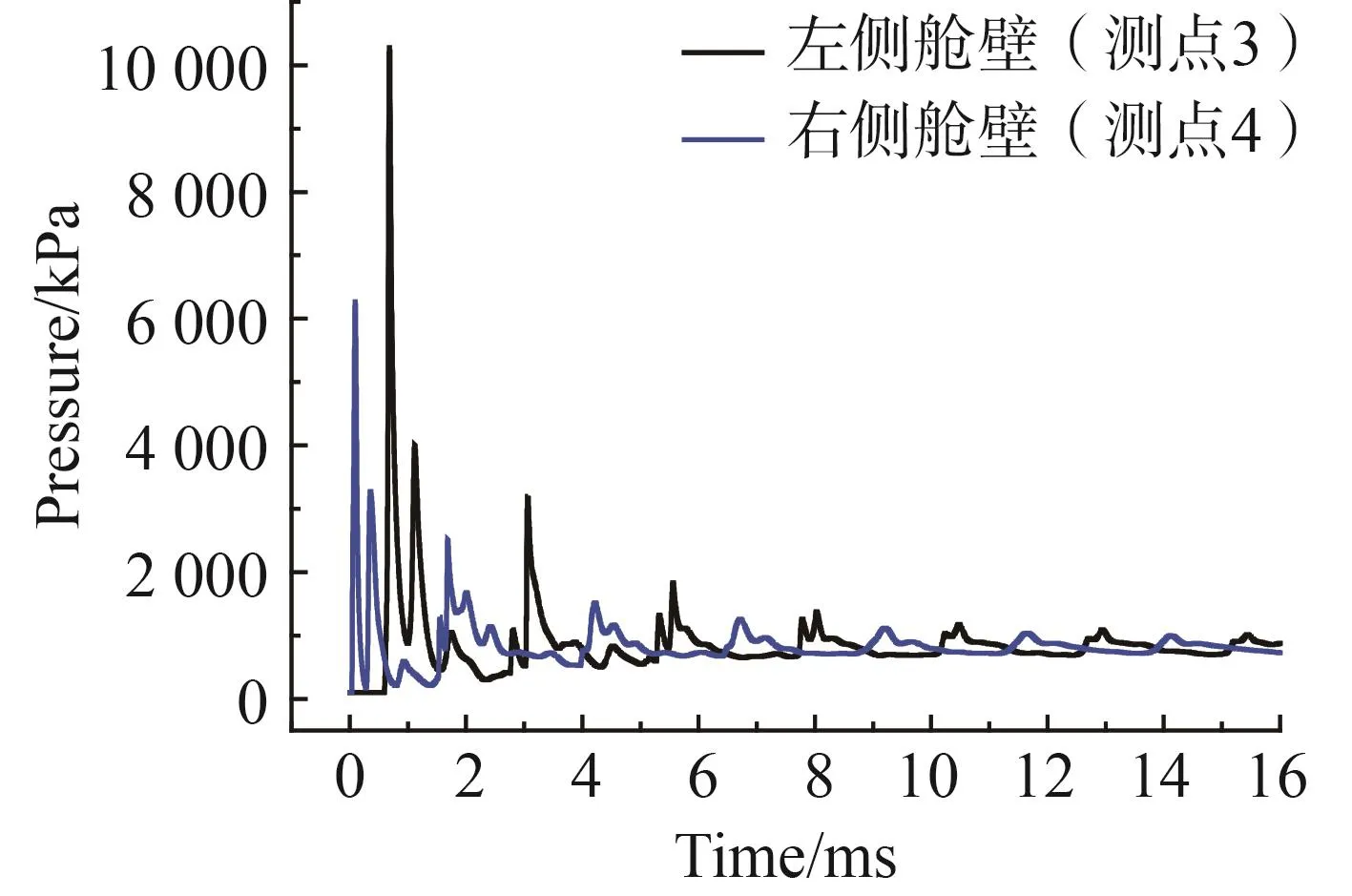
图8 测点处压力时程曲线Fig.8 Pressure temporal curves of measuring point

表6 不同时刻舱内典型压力云图Tab.6 Typical pressure cloud diagram of cabin at different time

图9 测点处冲量时程曲线Fig.9 Impulse temporal curves of measuring point
图9中在0.85 ms之后,作用于左侧舱壁的冲量总大于作用于右侧舱壁的冲量,随着舱内压力的稳定,两侧冲量差值也逐渐稳定,最后2条变化曲线近似平行均匀上升。通过对5种工况下16 ms时刻两横舱壁冲量进行统计,得到了冲量差随爆距比L1/L2的变化曲线,如图10所示。可以看到,随着L1/L2的增大,两舱壁冲量差值近线性增大。
4 结 语
本文采用数值分析的方法,通过改变舱内爆炸时的爆源位置研究了爆距对远爆端和近爆端舱壁变形挠度的影响,并针对某工况分析了舱内载荷的变化过程。基于上述研究,针对本文的舱室模型,得到以下结论:
1)当爆距比L1/L2>1时,远端舱壁的变形挠度总大于近端舱壁变形挠度,且随L1/L2的增大,两舱壁的变形挠度差逐渐增大。当爆距L1均匀增大时,远端舱壁的变形挠度也均匀增加,挠度增量约为爆距增量的11%,而近端舱壁的挠度变化不明显。
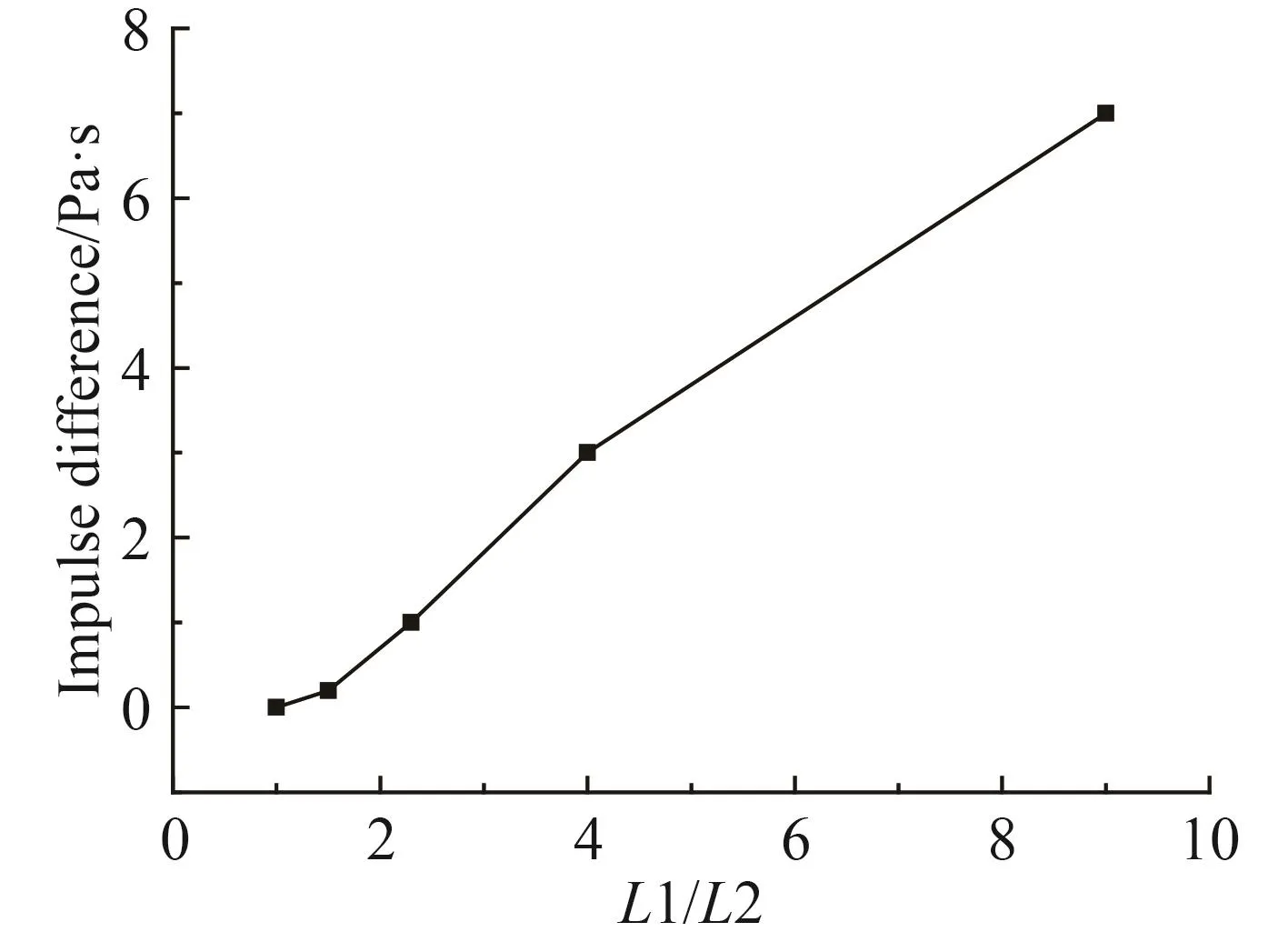
图10 16 ms时刻左右舱壁冲量差及挠度差随爆距比L1/L2的变化Fig.10 The difference of left and right buikhead impulse at 16 ms under different working conditions
2)当爆距比L1/L2>1时,舱内爆炸后作用于远端舱壁的冲击波不单是爆炸初始冲击波,还有来自近端舱壁及四周刚性舱壁的反射冲击波相互作用而形成的压力很大的叠加波。作用于远端舱壁的冲量总大于近端舱壁的冲量,且作用于两侧舱壁的冲量差值随着L1/L2的增大近线性增大。

