浅析模型与建模在高中生物教学中的实施


摘 要:模型在高中生物教材中的定义为:人们为了某种特定目的而对认识对象所作的一种简化的概括性的描述。使用模型可以对类似的、相关的内容形成联系,围绕模型解决问题会更简洁。模型的形式很多,包括物理模型、概念模型、数学模型等。
关键词:物理模型;概念模型;数学模型;建模
一、 物理模型
物理模型是以实物或图画形式直观地表达认识对象的特征。
(一) 图画模型
高中生物的图画模型包括很多,如细胞结构模型、有丝分裂过程模型、减数分裂过程模型等,在建模中,要注意实际操作,学生在观察这类模型时都能看懂,但是自己建模时总会出现一些细小的问题,所以要让学生亲身体验图画模型的绘制过程,老师对学生所建立的图画模型进行批阅、规范,從而使学生建立准确的图画模型,如分裂的图画模型,学生最初会把有丝分裂后期的染色体图画模型中的染色体着丝点方向画反,减数分裂又画不清楚同源染色体,经过教师的校正,才能让学生形成规范的图画模型,进一步形成正确的知识体系,加深知识理解。这类模型主要用于解决复杂结构或过程的直观化,使结构或过程清晰明了。
(二) 实物模型
高中生物的实物模型也比较多,如DNA双螺旋结构模型、细胞结构模型等,这类模型就需要学生动手操作了,利用生活中容易获得的材料,进行建模,从中体会生物知识的趣味,如构建DNA双螺旋结构模型时,可以利用针织的方式、用泡沫牙签做材料、用纸片图钉等。再比如做细胞结构模型时,可以用橡皮泥、面团、西瓜皮等等。将构建的模型进行展示,让学生们为自己的作品自豪的同时收获相关结构的立体认识,也有助于创造性思维的发展。
二、 数学模型
数学模型是用来描述一个系统或它的性质的数学形式。高中常用到公式、柱形图、曲线图、表格。
(一) 公式模型
它的形成要有推导过程,从而让学生信服,如Aa连续自交n代,子n代中杂合子所占的比例可以用1/2n进行表达,有了公式,再解决这类问题时就可以套用公式,使解题过程简化,提高解题速度。在如在解决基因频率与基因型频率时,有这样的公式(p+q)2=p2+q2+2pq,在合适的条件下,就可以根据题干信息套用公式解决相关精准计算的问题。
(二) 曲线图
它的构建常常会有相应的数据,根据数据进行构建,在建模中,首先要注意横纵坐标代表的含义,其次是坐标值,再次是曲线的走势与横纵坐标的对应关系。构建后的曲线图常常更直观的反映出数据的变化规律。如种群数量的J型增长,若用公式模型表示为Nt=N0λt,我们可以运用公式精确地计算出种群的数量,但是它的变化却并不直观,如果绘制曲线图则能更清晰看出随着时间的推移,种群数量是怎样不断增多的,曲线图能更清楚地表现出变化趋势。
(三) 柱形图
构建柱形图也要注意横纵纵坐标,另外用多个柱形表示多个因变量时要注意区分不同柱形所代表的含义,不要混淆。如研究光照强度对光合作用强度的影响时,分析呼吸作用强度与光合作用强度关系时要注意不同的因变量如何变化。从应用上与曲线图类似,只是不同的表达方式。
(四) 饼状图
饼状图常用来表示在一个整体中,各个方面所占的比例,如必修一第二章第一节元素的含量就是用它来表示的。它也能直观体现数据大小,应用比较局限,仅限于比例关系。
(五) 表格
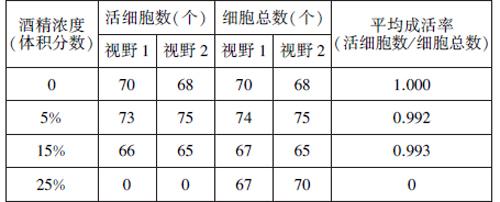
在高中生物中长用来作为实验结果的记录方法,在构建表格时,表格的第一行或第一列要表示出自变量、因变量,还要在自变量下表示出重复,有些还需要添加一定的数据处理。如为了了解酒精对细胞的毒害作用,某研究性学习小组开展了探究实验,记录结果如下:
用表格记录实验结果比较方便,但直观性不强,在进一步数据处理时,常常转化为曲线,二者常结合使用。
三、 概念模型
概念模型是指以文字表述来抽象概括出事物本质特征的模型。相比于前两种模型,概念模型的应用应该是最广泛的,生物的每个内容都存在概念,都可以用文字概括建模,它适用于每节课。构建概念模型的方式也比较多,如框架图、流程图、思维导图等,在构建中要找到合适的文字,用合适的文字来概括事物的本质特征。如:
运用概念模型对所学内容进行归纳概括,有助于知识的系统化,构建出知识之间的联系,简化冗长的内容。
模型与建模的思维方法是生物教学不可缺少的教学方法,通过教学指导,让学生拥有建模的方法,从而可以运用建模所形成的模型去解决实际问题,这是授之以渔的教学方法,是能让学生形成终生受用之思维能力,也是体验探索式的学习,将开启学生的智慧之门,引领学生进入更深层次的研究。
参考文献:
[1]中华人民共和国教育部.普通高中生物学课程标准(2017年版)[S].北京:人民教育出版社,2018.
[2]朱正威,赵占良.生物必修1·分子与细胞[M].北京:人民教育出版社,2018.
[3]朱正威,赵占良.生物必修3·稳态与环境[M].北京:人民教育出版社,2018.
作者简介:
李艳丽,黑龙江省伊春市,黑龙江省伊春市第一中学。

