正交各向异性CFRP材料的本构关系及其在平板撞击模拟中的应用

张 昆， 汤文辉， 冉宪文

(国防科技大学 文理学院，长沙 410073)

碳纤维增强树脂基类复合材料(Carbon-Fiber Reinforced Polymer, CFRP)以低密度、高比模量以及在高温高压等极端条件下良好的力学性能，在航空航天及军工领域获得了广泛的应用[1-2]，如用于制造航天飞机机翼，尾舵及导弹壳体等。在空天环境中，上述部件可能随时受到飞鸟，空间碎片等的高速撞击，相对撞击速度从几百米每秒到几千米每秒不等，因此研究该类材料在高速撞击下的动态力学响应行为，对于提高飞行器整体的安全系数具有重要意义[3-6]。通常这一类复合材料具有力学性能的各向异性，这会对材料的强度，屈服，及应力波传播等产生显著影响。与传统金属类材料相比较，数值计算上该类材料在本构模型及物态方程(Equation-of State, EOS)的处理上也较为复杂。对于准静态及低压情况，应力应变计算采用各向异性本构关系就能达到很好的效果。而对于动高压情况，需要引入物态方程来计算。值得注意的是，对于各向异性材料，在高压段材料的体积形变会对压力产生贡献，即材料的体变和形变发生耦合，因此对于这一类材料，EOS需要作出一定修正。对于这一问题，Anderson等[7-8]给出了考虑正交各向异性修正的静水压力及偏应力，并得到了多项式形式的Grüneisen物态方程，使得压力计算可以同时考虑高压下的体积压缩非线性及低压下不同方向的强度差异性。Lukyanov等[9-10]提出了一种对应力应变张量的广义分解方法，并同样采用Grüneisen物态方程进行了平板撞击问题的模拟计算。美国Sandia实验室的冲击动力学软件CTH[11]在正交各向异性复合材料的处理上收录了上述两种方法，但目前研究大多数采用了第一种修正模型。

对于CFRP类材料，在强冲击载荷作用下，压力的急剧升高会导致材料内部层裂产生及裂纹的扩展，这一损伤在宏观上表现为与金属材料屈服类似的不可逆形变。文献[12-13]对这一问题进行了研究，尝试采用Tsai-Hill屈服准则来描述碳纤维增强复合材料的不可逆形变问题。事实上屈服准则的选取对于材料塑性状态的判定及后续塑性应变计算具有重要意义，文献[14]对于各向异性材料的屈服准则选取进行了较全面的介绍。在塑性屈服准则在这一类材料的使用上，Anderson等采用了一种广义von-Mises屈服准则，并成功运用于冲击动力学程序EPIC92。蒋邦海等[15-16]完成了一系列从准静态到中高应变率加载下的某型碳纤维增强酚醛树脂材料(C/PF)的力学实验，得到了该材料的Tsai-Hill屈服准则参数并成功运用在一维下的高速撞击模拟中。基于此黄霞等[17-19]构建了该材料的二维各向异性动态本构模型，通过自行编写有限元程序实现了矩形，圆柱壳形靶板在平板撞击，X射线热击波辐照等外载荷加载下C/PF材料的热力学响应模拟。目前关于CFRP材料的平板撞击研究大多局限于一维或二维研究，而三维正交各向异性材料本构关系，物态方程的构建及其在动高压条件下的数值模拟计算中的应用鲜有文献报道。

基于上述情况，本文以文献[20]中C/PF材料为研究对象，建立了一套完整的三维各向异性材料本构模型，在此基础上编写了一显式拉格朗日有限元程序，对一有限尺寸平板撞击问题进行了数值计算。

1 理论模型

1.1 弹性段本构关系

对于CFRP类材料，碳纤维作为增强基承担了绝大部分的力学载荷，因此碳纤维的力学性能及其编织方式决定了材料整体的力学性能。本文所研究C/PF材料是由碳纤维二维正交平纹机织成碳布后层叠，再加入酚醛树脂热压固化生成。在主轴坐标系下材料存在三个力学主轴方向，分别为碳纤维经向，碳纤维纬向，碳布厚度方向，如图1所示。

图1 C/PF材料示意图Fig.1 A schematic of C/PF material

三维应变条件下， 弹性段应力分量σij与应变分量εij的本构关系采用广义Hook定律描述

(1)

式中：Cij为刚度矩阵系数，其分量由材料在三个主轴方向上的杨氏模量、泊松比及剪切模量确定。对应力及应变进行球-偏分解，正交各向异性材料弹性段的静水压p表示为

(2)

(3)

(4)

1.2 塑性本构模型及Tsai-Hill屈服准则

当材料应力状态在应力空间超越屈服面时，材料进入塑性变形阶段。根据塑性增量理论，应力是过程量与应变历史相关，而应力增量[dσ]与弹性应变增量[dεe]之间仍满足广义Hook定律

[dσ]=[C][dεe]=[C]([dε]-[dεp])

(5)

式中： [C]为刚度矩阵； [dε]为应变增量张量； [dεp]为塑性应变增量张量。同样对[dσ]进行分解，得到塑性段内压力增量为

(6)

可以看到，在塑性段压力不但与体应变相关，同时也会受到偏应变增量及塑性应变增量的影响。对于塑性应变的计算，材料的应力状态始终在屈服面上，根据正交性法则和一致性法则，塑性应变增量可表示为

(7)

式中： [∂F/∂σ]为塑性势函数即屈服函数对应力的偏导张量。对于正交各向异性复合材料。本文中对于C/PF材料采用一9参数平方形式的Tsai-Hill准则

(8)

(9)

式中：Yij分别为主轴方向上的单轴压缩强度和相对应方向上的纯剪强度。λ为塑性流动因子

(10)

1.3 Grüneisen物态方程(EOS)的修正

在式(6)中， dpp与θ之间的线性关系只有在低压段成立。在高压下，二者之间呈非线性关系，因此需要额外引入物态方程来计算压力。固体材料压缩常采用Grüneisen物态方程

p=pH(v)+ρΓ(e-eH)

(11)

式中：ρ为密度；v为比体积；e为比内能；Γ为Grüneisen系数；pH,eH组成冲击压缩线。

(12)

(13)

式中：c0和s为Hugoniot参数；ρ0为初始密度；v，v0分别为当前及初始比体积。定义压缩比

(14)

在小应变条件下忽略应变高次项有

(15)

对式(11)做关于μ的多项式展开，三阶截断并代入式(15)，得到多项式形式的物态方程为

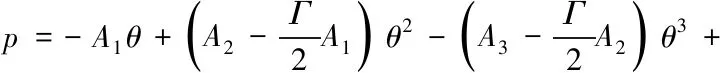
(16)

其中，各项参数可表示为

(17)

对式(16)求全微分，得到增量形式的压力dp为

(18)

式(16)和式(18)目前仅仅适用于各向同性材料，并没有反映材料的各向异性特点。对于冲击动力学问题，压力由物态方程计算，在低压弹性段，由本构关系得到的pe的表达式(6)应当是物态方程式(18)在低压下的极限情况，同时也要考虑到高压段偏应变及塑性应变增量对压力的影响，因此对式(15)可做如下修正：①用广义体积模量A′替换物态方程中体应变一阶项系数A1(事实上A1即为传统体积模量)；②在方程中添加偏应变对压力贡献项；③方程中添加塑性应变对压力贡献项。基于上述修正可得到正交各向异性修正下的压力为

(19)

目前涉及到正交各向异性CFRP材料的本构方程及物态方程的研究，在工程上多采用与式(16)相似的体应变全量的多项式形式，或只考虑了偏应变项而忽略塑性应变项的影响[21]。而本文给出的三维应变条件下正交各向异性的本构模型能充分体现压力随体应变的非线性关系，同时材料正交各向异性力学性能对压力的各个影响因素也已考虑在内。在后续计算中本文将对各个修正项的影响进行定量分析。

2 算例及分析

为了对本文提出的模型进行验证，本文对该材料的平板撞击(Planar Plate Impact, PPI)问题进行了模拟。初始设定靶板及飞片中碳纤维经向，纬向及碳布厚度三个主轴方向依次与实验室坐标系下xyz坐标轴方向重合，靶板与飞片尺寸相同均为0.25 cm×1.0 cm×1.0 cm。飞片沿x坐标轴方向，以速度w撞击静止放置的靶板，如图2所示。

图2 平板撞击实验示意图Fig.2 A schematic of planar plate impact experiment

有限元前处理采用Ansys生成标准.k格式文件进行读入，网格尺寸为0.012 5 cm×0.025 cm×0.025 cm。计算采用自行编写的显式动态拉格朗日描述有限元程序[22]。材料物态方程参数为：ρ0=1.38 g/cm3，c0=2.35 km/s，s=1.66，Γ=2.32。材料在其主轴方向的力学参数及屈服函数参数见表1和表2。

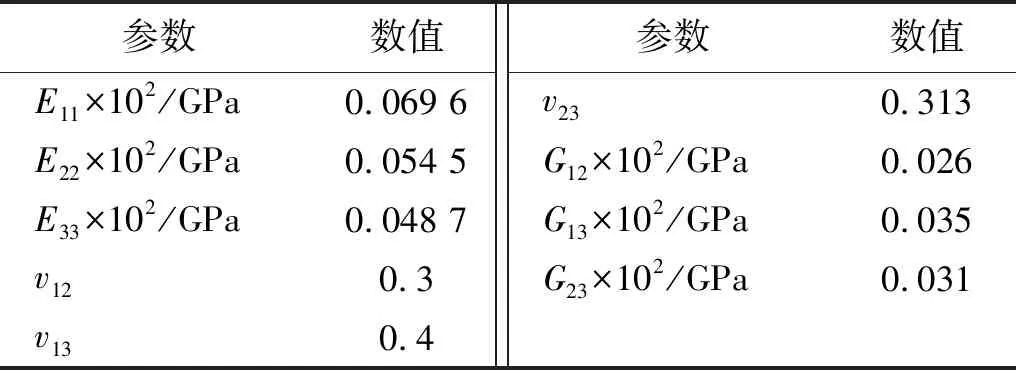
表1 C/PR材料在主轴方向上的力学参数Tab.1 Mechanical parameters of C/PR material in principal axis directions

表2 C/PR材料在主轴方向上的Tsai-Hill屈服准则参数Tab.2 Tsai-Hill yield parameters of C/PR material in principal axis directions GPa

以飞片速度w=1 500 m/s为例，图3和图4分别给出飞片与靶板整个模型在t=0.3 μs时刻的三维压力分布以及z=0.5 cm处xy平面内压力分布。

图3 飞片及靶板三维压力云图Fig.3 3D contour of pressure in flyer and target

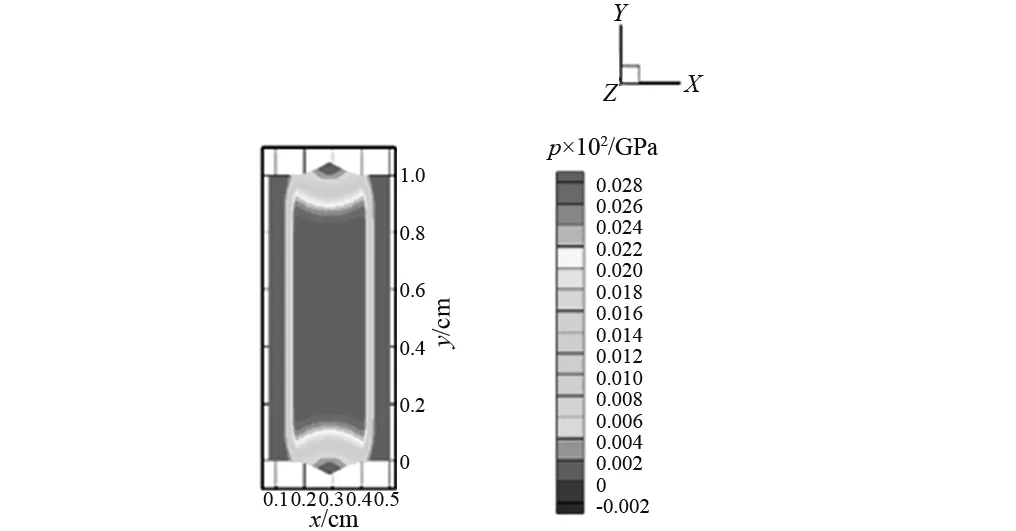
图4 xy截面压力云图Fig.4 Contour of pressure in xy section

从图3和图4可以看出，碰撞发生后对称的压力波分别向靶板及飞片的前后自由面处传播，同时在碰撞面附近产生了材料的挤压变形和侧向膨胀，在碰撞面周边的边侧自由面上产生了侧向稀疏波，波的传播呈现出明显的三维效应。

图5给出了该时刻，飞片-靶板中轴线上的三个主应力分布情况。可以看到，中轴线上三个主应力的分布并不相同，x方向即碰撞方向应力值最高，y方向应力高于z方向应力。这是因为碳纤维纬度方向与碳布厚度方向这两个主轴方向虽都与速度方向垂直，但不同主轴方向上的模量，泊松比等存在明显差异，经计算得到的主应力也完全不同。这一应力分布显著不同于各向同性材料，反映了各向异性材料的力学特点。

为了对本文所建立本构模型做进一步分析，在上述工况下本文比较了采用原始各向同性物态方程式(18)及修正后的物态方程式(19)计算的结果。t=0.3 μs时刻靶板中轴线上的压力分布如图6所示。

取靶板内中轴线上距碰撞面0.068 cm处的单元作为观测点，记录得到两种模型的压力历史曲线如图7所示。

图5 中轴线应力分布Fig.5 The distribution of stresses alone the axis

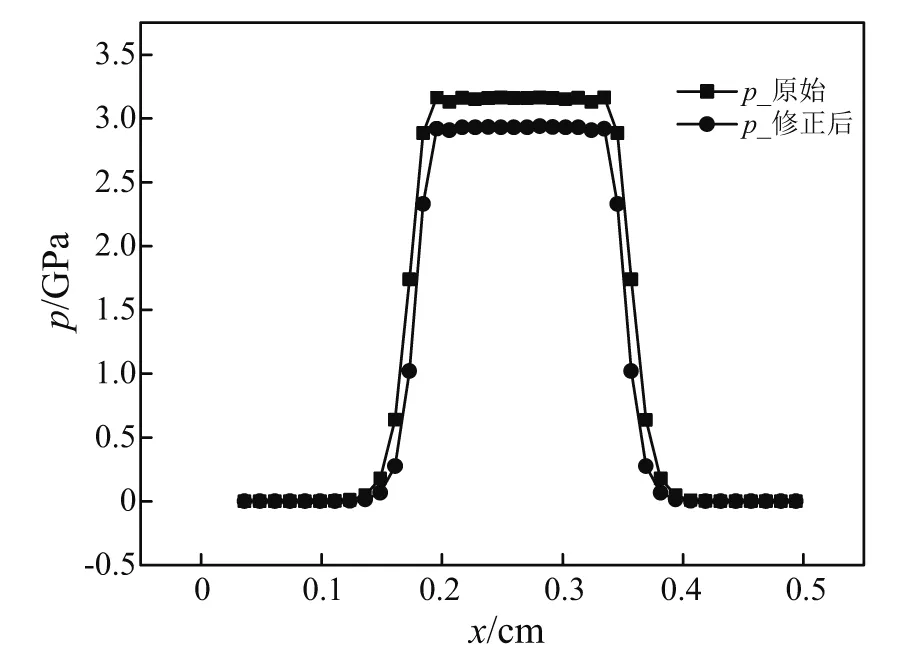
图6 压力沿轴线分布Fig.6 The distribution of pressure alone the axis of two models

图7 固定点处压力历史曲线Fig.7 The history curve of pressure at the fixed point

从图7可以看到，无论从某一时刻压力的空间分布还是固定点处的压力历史曲线都显示采用原始物态方程计算得到的压力较高。为了更进一步分析这一差异特性与飞片加载速度的关系，本文设定飞片速度从100～3 000 m/s，对这一平板撞击实验行了多次数值计算，计算结果见表3。

表3 不同飞片速度下原始物态方程及修正物态方程计算结果Tab.3 Results of the original EOS and modified EOS with different flyer velocity

当w=100 m/s，压力相对偏差最大达到27.2%，随着飞片速度增加逐步降低。当飞片速度达到3 000 m/s时，压力的相对偏差小于3%，两种模型计算结果趋于一致。本文分析认为，对于平板撞击问题，低速低压段，材料的体应变较小，此时p与θ近似成线性关系，比例系数为体模量。式(18)和式(19)得到的体积模量A1与广义体积模量A′分别为7.62 GPa和4.76 GPa差异较大，因此在低速状态下，两种模型压力相差较大。

图8 压力相对偏差随飞片速度的变化规律Fig.8 Variation of p relative error with the velocity of flyer

随着飞片速度w的上升，材料体应变增加，θ的高阶项对压力的影响随之增大， 压力p与体应变θ成非线性关系。而两种模型中表征高压下材料特性的物态方程参数ρ0，c0，s，Γ是相同的，即p与θ的二阶三阶关系是一致的。因此两种模型在低压段差异较大而高压区趋于一致的计算结果是合理的。另一方面，为了定量的研究偏应变修正项及塑性应变修正项对压力的影响，因此本文分别定义

(20)

(21)

其中积分时间为0时刻至压力稳定为平台压力的时刻ts。从表3数据计算可得，在w=100 m/s时，偏应变修正项p_εd对压力p的贡献绝对值最高， 接近-10 %。但随着速度的上升，p_εd的绝对值增高但在压力中所占百分比下降，材料在高压下呈现出流体特性，各向异性特性趋于消失。而塑性应变项p_εp对压力的贡献在计算中均未超过-2%，所占百分比非常有限，因此在各个阶段的计算中均可以忽略不计。

3 结 论

(1) 基于弹塑性理论，从广义Hook定律出发，导出了正交各向异性材料在弹性和塑性阶段应力增量与应变增量之间的关系式；采用Tsai-Hill准则描写了各向异性材料的塑性应变增量；采用Grüneisen物态方程描述了压力与体应变之间非线性关系。

(2) 将正交各向异性材料的三维本构模型与三维有限元计算结合起来，对C/PR正交各向异性材料飞片与靶板的碰撞过程进行了数值模拟。结果表明，所建立的本构模型能够反映出材料力学性能的各向异性特性。

(3) 数值模拟结果表明，飞片速度较低时，正交各向异性模型得到的压力显著小于各向同性模型。随着飞片速度升高，平台压力上升，两种模型计算结果趋于一致。

(4) 对于正交各向异性模型中引入的偏应变修正项，在低压条件下会对压力产生一定影响。而塑性应变增量项无论飞片速度高低，均可忽略而不造成太大误差。