基于半解析法的圆柱壳结构自由振动特性分析

李海超， 庞福振， 田宏业， 刘江涛

(哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

柱壳结构被广泛应用于航空航天、船舶、化工、机械等领域，因此开展一般边界条件下柱壳结构自由振动特性分析，明确其自由振动特性规律，对丰富圆柱壳结构基础理论及指导工程应用具有重要的意义。在此方面，Rayleigh[1]对光圆柱壳的拉伸振动和弯曲振动进行了研究，给出了无限长圆柱壳在真空环境中的自由振动固有频率计算公式。Galletly等[2]采用数值算法求解不同端部结构的圆柱壳的自由振动。Cheng等[3]以圆柱壳-圆板为模型，采用Rayleigh-Ritz法求解特征值方程从而求解其自由振动特性。骆东平等[4]采用Flügge和有限差分法，以环肋增强圆柱壳为研究对象。Yu[5]讨论了简支和固支边界条件下有限长圆柱壳的自由振动特性。王宇等[6]基于Love壳体理论对固支-自由约束条件下受径向载荷的薄壁圆柱壳构件开展受迫振动响应特征分析。汪志强等[7]采用Flügge经典薄壳理论和波传播方法讨论了正交各向异性圆柱壳的自由振动问题，且所提出方法可考虑正交各向异性圆柱壳在复杂和受外力的情况。向宇等[8]提出了一种半解析方法，求解饱和多孔介质圆柱壳动力学问题。Li等[9]依据Flügge薄壳理论建立振动分析模型，采用Jacobi-Ritz法分析了均厚度以及变厚度圆柱壳、球壳等组合壳体结构的自由及受迫振动特性。庞福振等[10]基于Flügge壳体振动理论，将改进精细传递矩阵法应用于水下加筋柱壳声辐射问题，分析了经典边界条件、结构损耗因子、流体介质以及壳体厚度对结构声辐射的影响。Pang等[11]提出了一种求解双曲率壳自由振动的半解析方法。对于区域能量分解法，最重要的是广义变分原理理论的成熟，我国著名数学和力学家钱伟长[12]对广义变分原理进行了系统的研究，对广义变分原理成熟应用起到了极大的推动作用，也为区域分解法在弹性体中的应用提供了坚实的基础。Zienkiewicz等[13]在其《有限元法》一书对变分约束条件进行了讲解，确定拉格朗日乘子系数，并应用到弹性力学中。宋文煜[14]应用区域分解法，分别研究了钻柱纵向、扭转、横向以及耦合振动的固有频率及长度、钻柱壁厚等对钻柱固有频率的影响。Zhou等[15]提出了一种求解圆柱和实心圆柱自由振动的通用方法。分析过程基于小应变、线性和精确弹性理论。利用Chebyshev多项式级数乘以边界函数满足几何边界条件作为可容许函数，应用Ritz法导出了圆柱的频率方程。

由以上分析可知：一方面现有文献对任意边界条件下圆柱壳自由振动特性研究较少；另一方面，现有研究方法尚未形成统一的形式，且现有半解析方法仍有待进一步丰富。为此，本文基于区域能量分解法，开展圆柱壳自由振动特性分析，旨在提出统一的求解公式，为任意边界条件圆柱壳自由振动特性分析提供数据积累和方法依据。此外，运用区域能量分解法时，可通过改变边界控制参数可快速地分析不同组合边界条件下壳体的振动特性，无须重新形成整个壳体的质量和刚度矩阵，从而大幅提高计算效率。

1 柱壳结构区域能量分析模型的建立

本文基于区域能量分解方法的基本原理，对其进行深度扩展，并运用到求解柱壳结构的振动特性当中。圆柱壳示意图如图1所示，结构的长度为L，半径为R，壳体厚度为h，结构的坐标系统如图1所示。

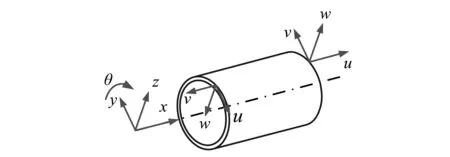
图1 柱壳结构的理论模型Fig.1 Theoretical model of cylindrical shell structure

1.1 柱壳结构的能量泛函建立

将圆柱壳体沿圆柱的轴线方向均匀地截断成NL段，即每一段的长度Li=L/NL。根据修正的Hamilton原理，考虑到每一段的能量和相邻两段之间的影响，圆柱壳体的总势能为

(1)

式中：TL,i，UL,i，WL,i分别为圆柱壳体的第i段的动能、应变能、外力功和附加能量泛函；ΠK,L为相邻分段i和i+1之间的附加界面势能。

当忽略圆柱壳体旋转惯性的条件下，圆柱壳体的第i段的动能可以表示为

(2)

式中：ui，vi，wi分别为不同方向的位移矢量；ρ为结构的质量密度；hi为第i段的结构厚度；Si为结构中面面积。

根据Reissner-Naghdi’s线性薄壳理论，i分段的最大结构应变能可以表示为

(3)

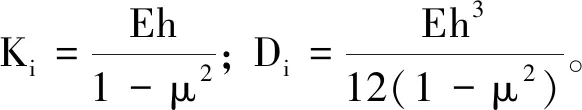
假设外部载荷全部作用在中面位置处，圆柱壳结构的第i分段分布着沿x方向、θ方向、z方向外力fu,i,fv,i,fw,i，此时结构第i分段的外力作功为

(4)

圆柱壳体的第i段、第i+1段的界面上的附加能量泛函为

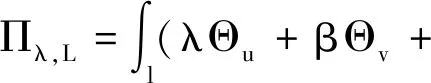
(5)

式中：λ,β,ϑ,ψ分别为柱壳结构分段i与i+1交界面处的未知拉格朗日乘子；Θu,Θv,Θw和Θr分别为柱壳结构分段i与i+1交界面处位移协调方程，它们可以表示为

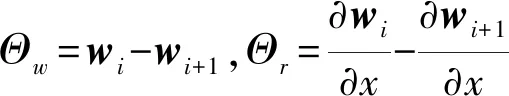
(6)

将式(2)～式(5)代入式(1)，并且根据广义变分原理，对ui，vi，wi，ui+1，vi+1，wi+1，∂wi/∂x，∂wi+1/∂x，λ，β，ϑ和ψ做变分运算，可得到

(7)

(8)

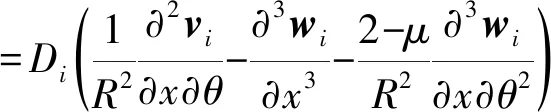
(9)

(10)

将式(7)～式(10)代入式(1)后得到新的能量泛函

(11)

式中：Nx=λ；Nθ=β;Qx=ϑ;-Mx=ψ。

为了保证数值算法的计算稳定性，在式(11)的基础上添加一项子结构交界面位移连续方程的最小二乘加权参数残值Πκ,L，此时结构的完整能量泛函表示为

(12)

(13)

式中：κu,κv,κw和κr分别为柱壳分区后第i段和第i+1段分区界面加权参数。

在式(13)中引入边界条件控制参数ςu，ςv,ςw,ςr, 通过控制参数的选取来控制边界条件。此时的能量泛函可以表示为

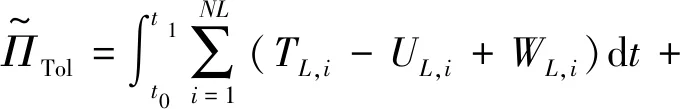
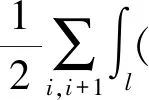
(14)

表1给出了边界条件控制权参数，通过选择不同的权参数来得到不同的边界条件。

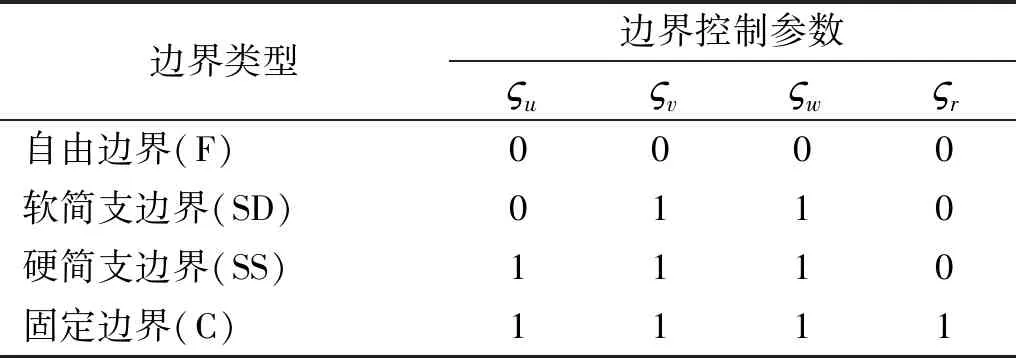
表1 不同边界条件对应的控制参数 ςt(t=u,v,w,r)Tab.1 Control parameters ςt(t=u,v,w,r)corresponding to different boundary conditions

1.2 位移函数的表达式

对于柱壳结构，柱壳结构的位移函数采用Chebyshev行列式[16]和傅里叶级数进行展开，系统的位移可以写成

(15)

(16)

(17)

式中：P为圆柱壳母线方向上位移分量的Chebyshev多项式截断值;N为壳体周向位移分量的Fourier级数截取阶数；Φp(x)为Chebyshev多项式，表示圆柱壳体轴向阶数;fni(θ)为傅里叶级数，表示圆柱壳体周向波数，它们分别表示为

Φ0(x)=1,Φ1(x)=x,Φi+2(x)=2xΦi+1(x)-Φi(x)

(18)

fn1(θ)=cos(nθ)+sin(nθ)

(19)

fn2(θ)=sin(nθ)+cos(nθ)

(20)

fn3(θ)=cos(nθ)+sin(nθ)

(21)

2 柱壳结构的振动特性分析

2.1 柱壳结构自由振动特性方程的求解

由“1.1”节可知，结构的整体能量泛函可表示为

(22)

对自由振动而言

(23)

对未知位移系数进行变分运算，此时可得到结构的自由振动特性方程

(24)

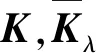
(25)

其中，

(26)

(27)

(28)

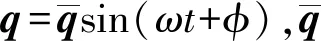
(29)

对式(29)求解，即可得结构的模态阵型。为统一表述，下文无量纲公式定义为

Ω=ωR(ρ(1-μ2)/E)1/2

(30)

2.2 最小二乘加权参数与分段数的收敛性研究

本节选取结构参数为：L=6 m，R=1 m，h/R=0.01，E=210 GPa，ρ=7 800 kg/m3，μ=0.3。弹性参数取值设为ku=kv=2×108N/M[17]，位移容许函数在母线方向上的切比雪夫正交多项式的截断值为8，结构的分段数NL=2。F-E边界条件下最小二乘加权参数收敛性分析如表2所示。

由表2可知，当加权参数增大时，结构的固有频率也随之增大，然而当加权参数达到某一个临界取值时，结构的计算结果已趋于稳定，在实际数值计算中，加权参数的取值不可能无穷大，因此，加权参数取临界值即可。从表2可以看出，当κ取值1×1012时，已达到临界值，但为保证计算的绝对数值稳定性，在后续的计算中，最小二乘残差加权系数取值为κ=1×1014。

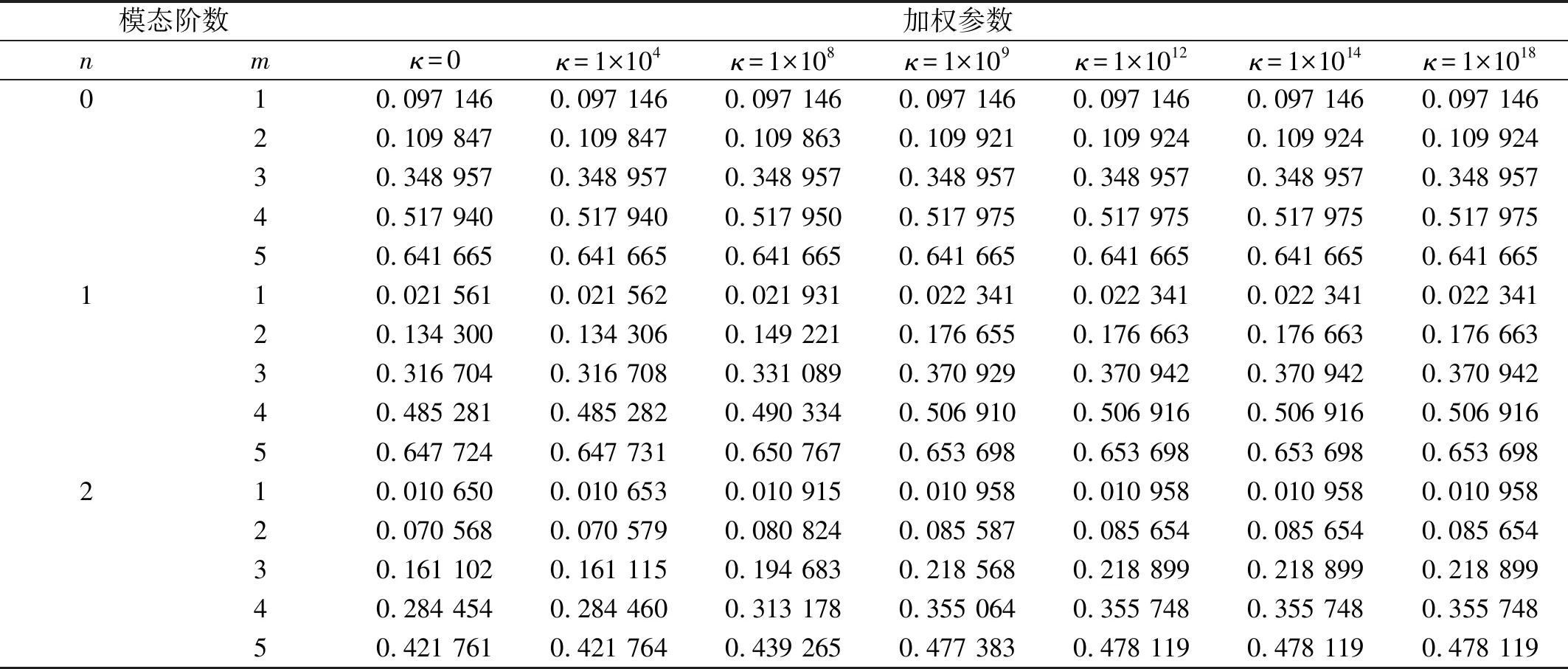
表2 最小二乘加权参数收敛性分析Tab.2 Convergence analysis of least squares weighted parameters

为兼顾求解精度和计算效率，需开展区域分段收敛性分析。选取结构参数与表2保持一致，并且加权参数取值为κ=1×1014。同时，为验证本文方法有效性，将本文计算方法与有限元法进行了对比，不同分段数下结构无量纲化固有频率Ω如表3所示。

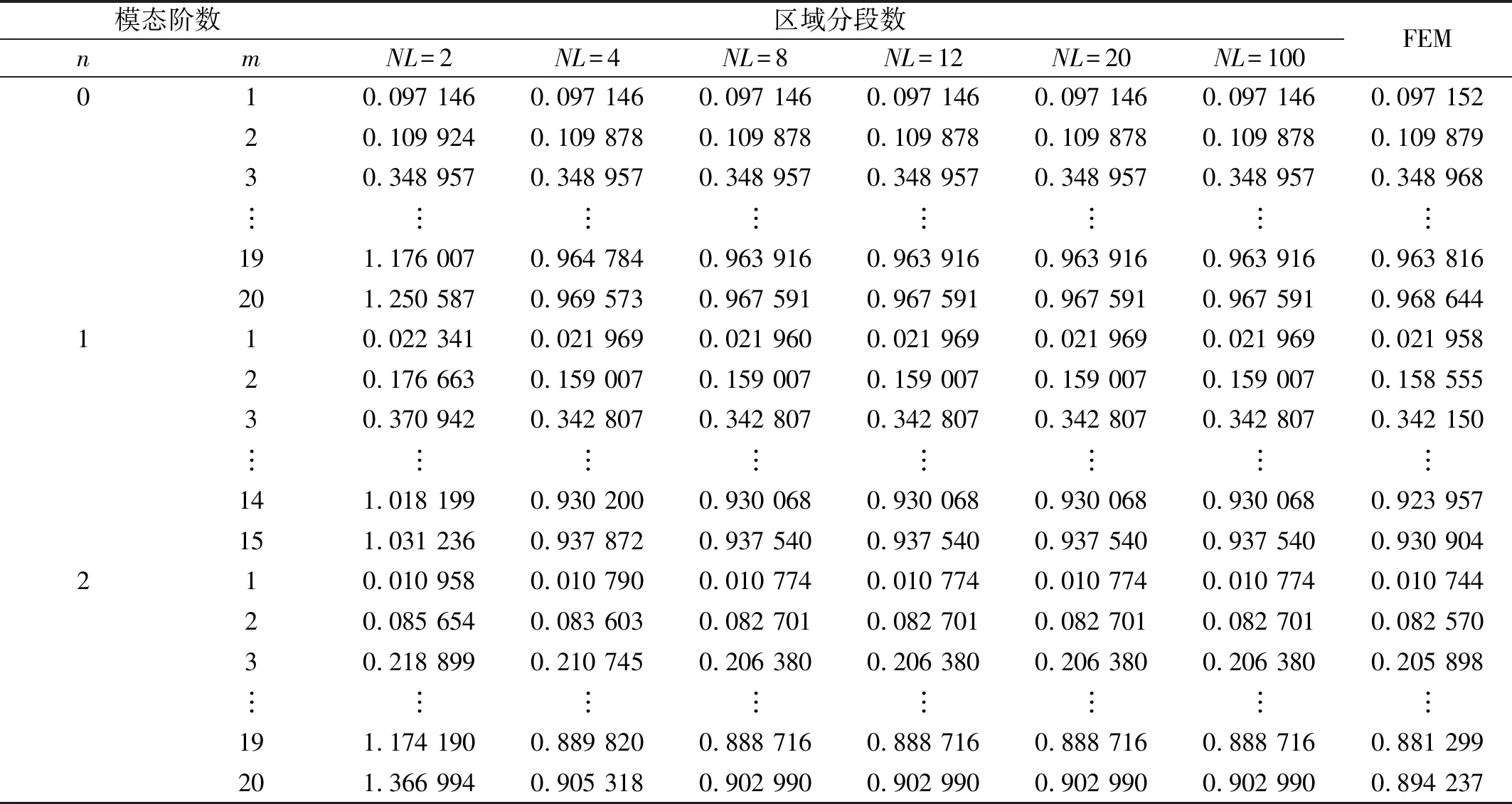
表3 区域分段数收敛性分析Tab.3 The convergence analysis of the number of regional segments

从表3可知，当NL=8时，其计算结果已收敛，且与有限元法相比具有较高的计算精度。因此，在后续的计算中，如不做特别说明，其分段数取值为NL=8。

3 柱壳结构自由振动特性分析

3.1 经典边界条件

在前文研究基础上，本节主要对经典边界条件(C-C)下的结构自由振动特性进行计算分析。结构的材料参数为：E=210 GPa，ρ=7 800 kg/m3，μ=0.3。结构参数与表2相同。两端固支边界条件下结构频率参数计算结果如表4所示。

从表4可知，在C-C边界条件下的计算结果与文献的计算结果和有限元仿真结果吻合良好，为进一步验证本文方法的有效性，计算S-S,F-F,F-S,C-S边界条件下的频率参数Ω，并与其他文献结果对比，其对比结果如表5所示(圆柱壳几何参数及材料参数与文献中圆柱壳相同，h/R=0.05，R/L=0.05，m=1)。

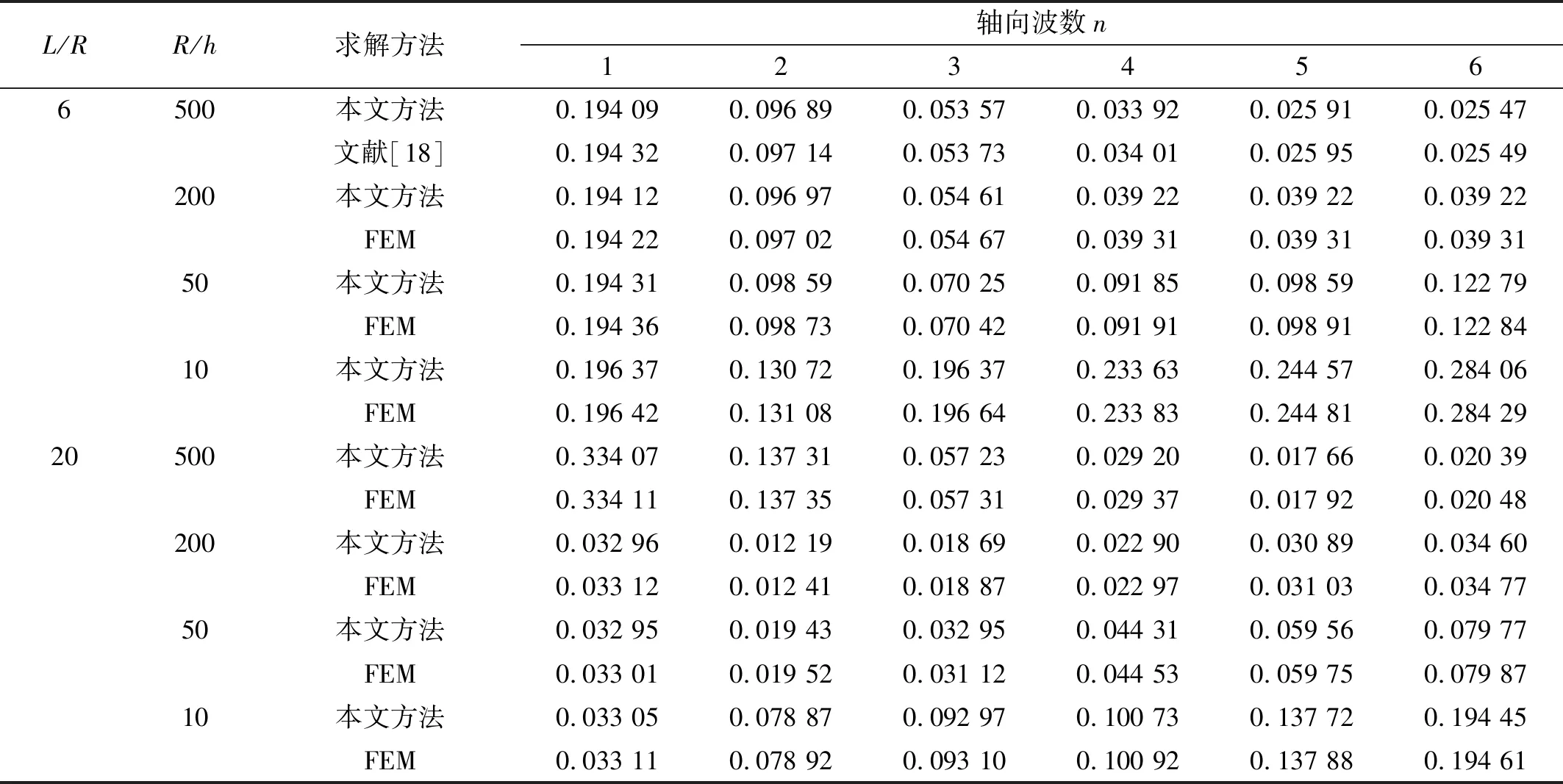
表4 圆柱壳在C-C边界条件下结构频率参数ΩTab.4 Structural frequency parameters Ω of a cylindrical shell under C-C boundary condition

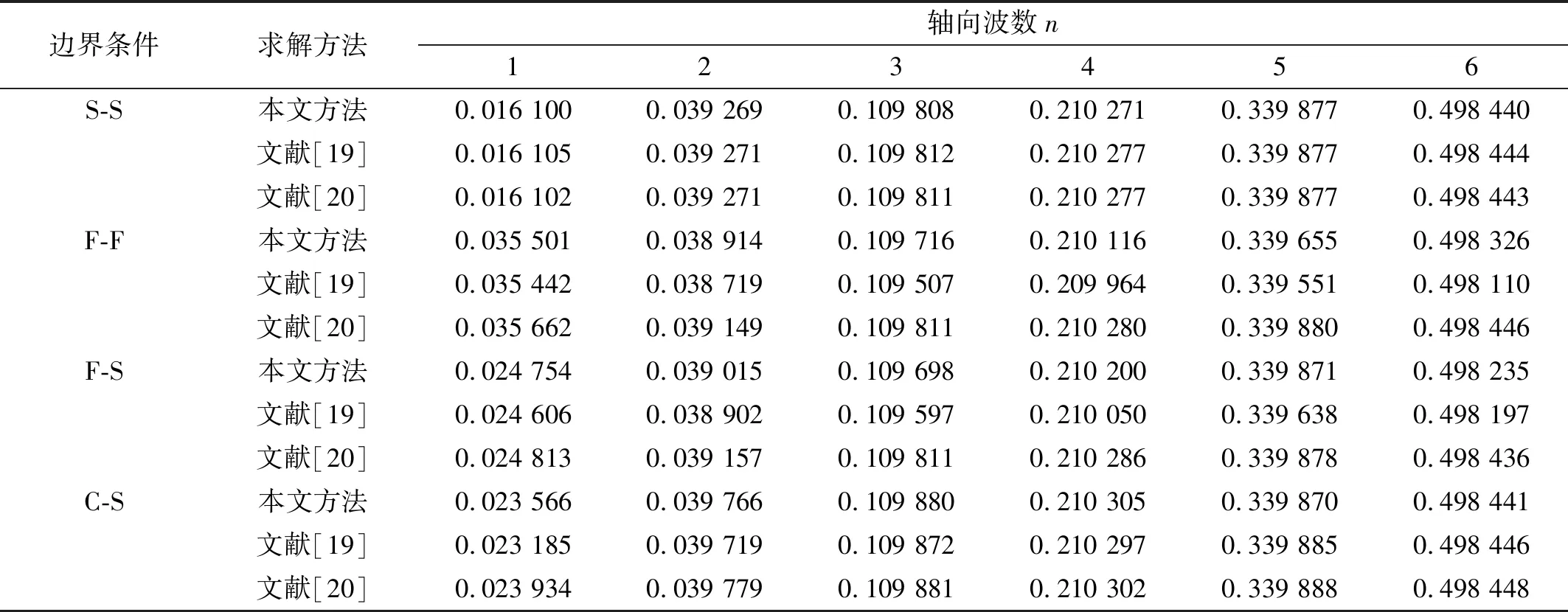
表5 圆柱壳在不同边界条件下文献对比结果Tab.5 Comparison of cylindrical shells under different boundary conditions

从表5中对比结果可以看出，在不同边界条件下，本文方法计算结果与文献对比结果吻合良好，更进一步说明本文方法的有效性。

3.2 一般边界条件

在前文研究基础上，本节主要对圆柱壳结构一般弹性边界条件下的自由振动特性进行研究。材料参数及结构参数与“3.1”节相同。使用区域能量分解法，可通过改变边界控制参数快速形成不同组合边界条件，这也是本方法的优势之一。首先定义三种弹性边界：E1弹性边界，其中只有u向为弹性约束，其余为固定边界条件(u≠0,v=w=∂w/∂x=0)；E2弹性边界，其中只有v向为弹性约束，其余为固定边界条件(v≠0,u=w=∂w/∂x=0)；E3弹性边界，其中只有v向与u向为弹性约束，其余为固定边界条件(v≠0,u≠0,w=∂w/∂x=0)。在u向的弹性约束刚度值大小为κu=4×106N/m，在v向的弹性约束刚度值大小为κv=8×106N/m。表6～表8给出了E1-E2,E1-E3,E2-E3边界条件下结构的无量纲频率参数。

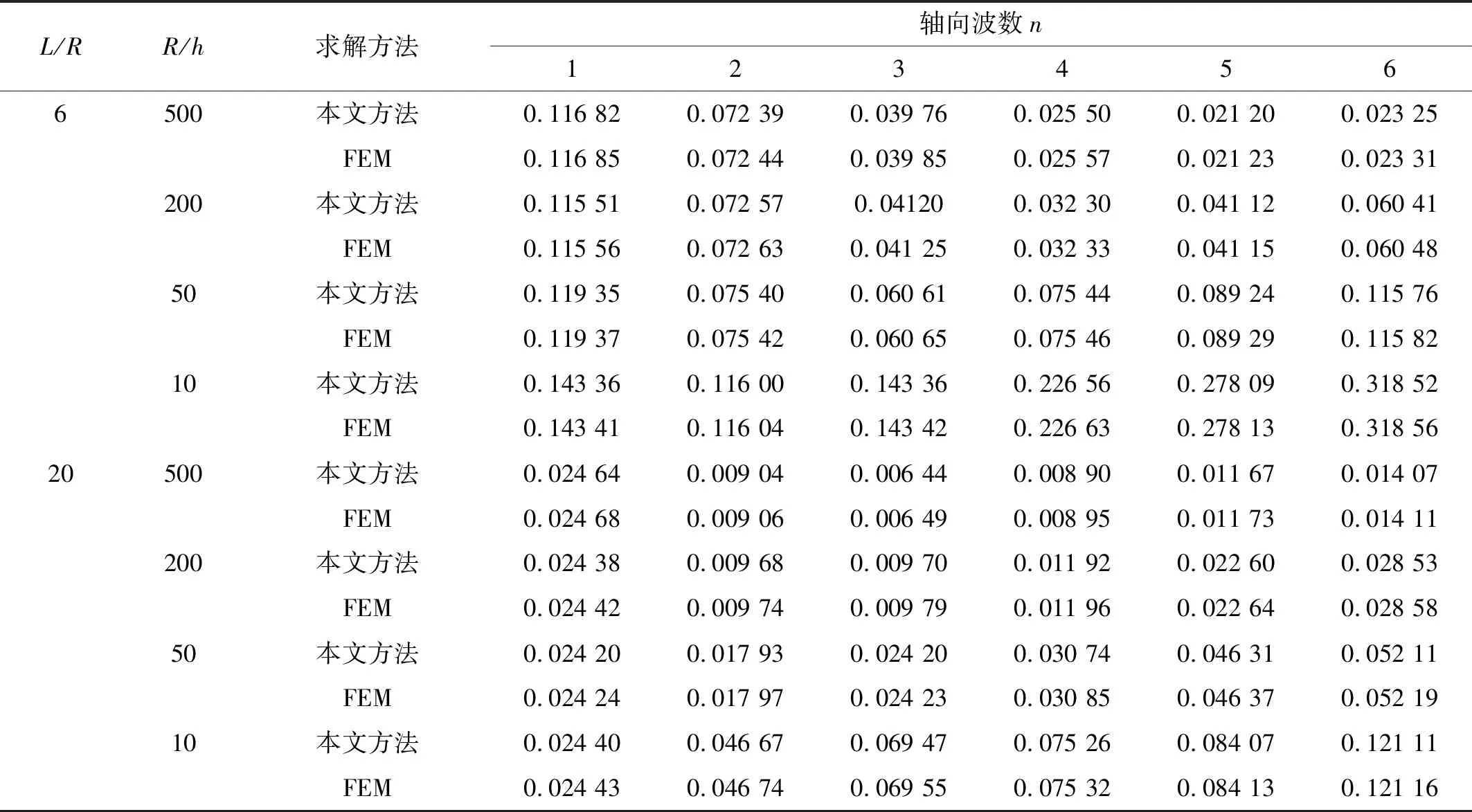
表6 圆柱壳在E1-E2边界条件下频率参数ΩTab.6 The frequency parameters Ω of a cylindrical shell under the E1-E2 boundary condition

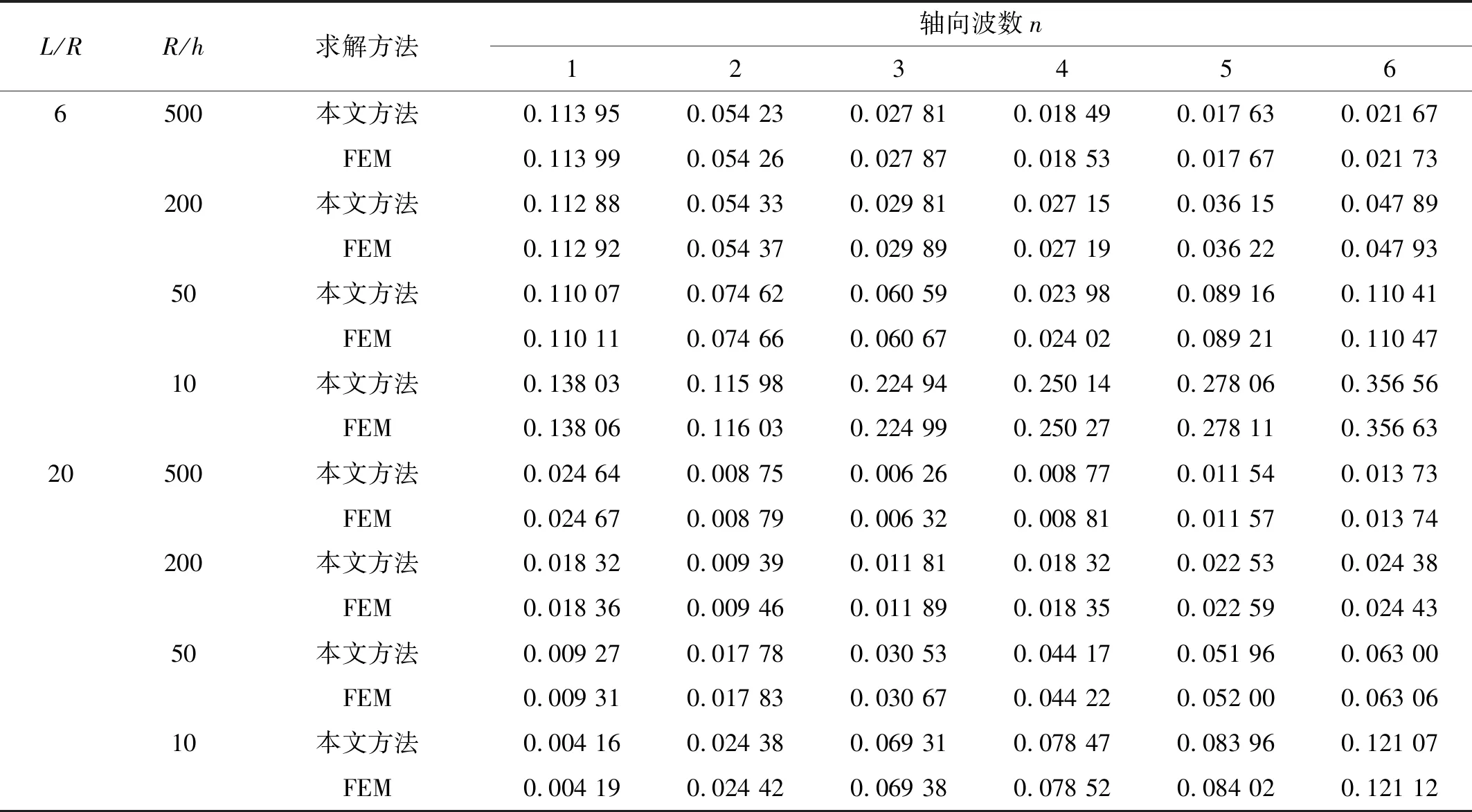
表7 圆柱壳在E1-E3边界条件下频率参数ΩTab.7 The frequency parameters Ω of a cylindrical shell under the E1-E3 boundary condition

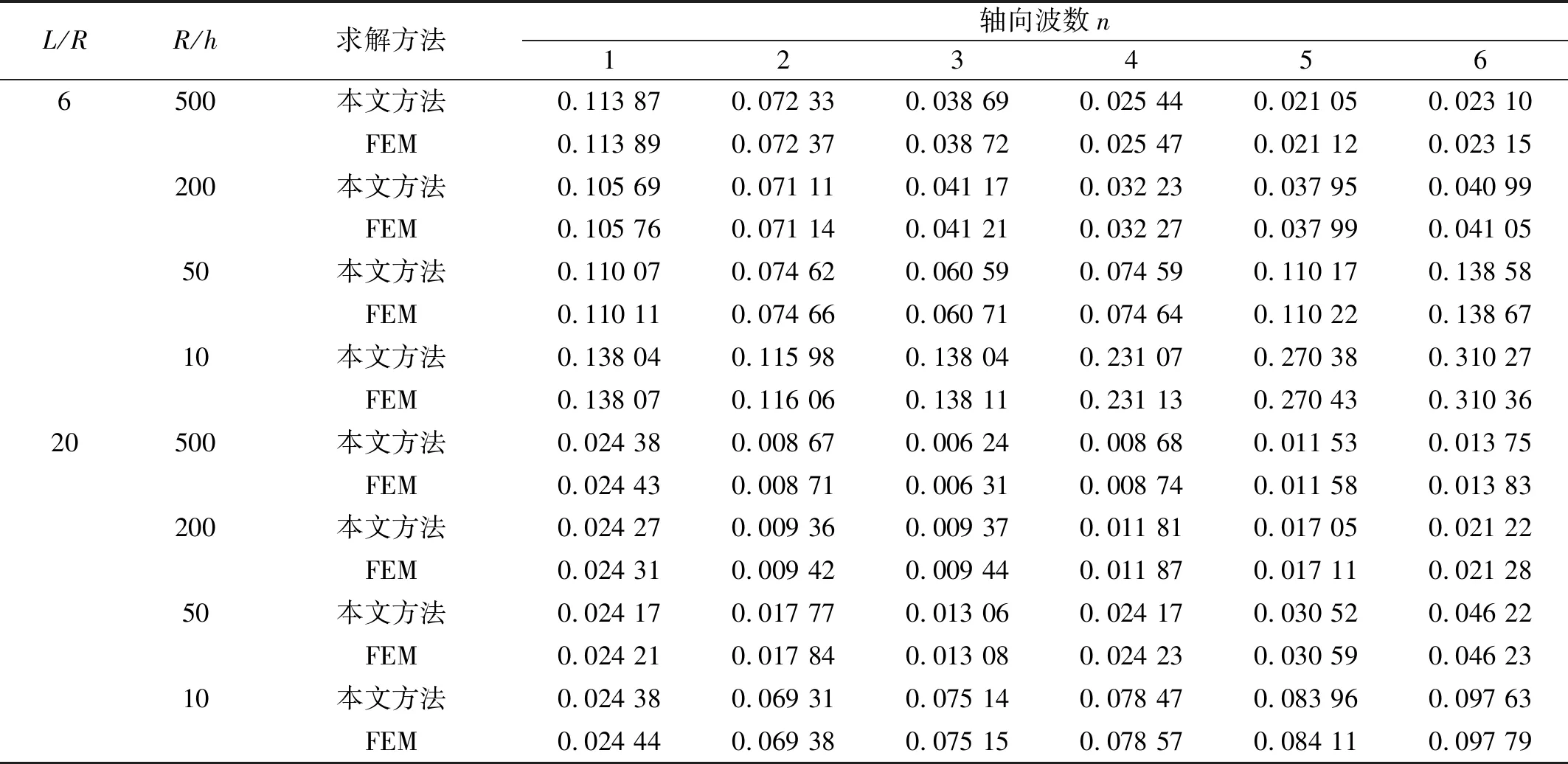
表8 圆柱壳在E2-E3边界条件下频率参数ΩTab.8 The frequency parameters Ω of a cylindrical shell under the E2-E3 boundary condition

由表6～表8可知，在弹性边界条件下，本文的计算结果与有限元计算结果吻合良好，说明本文方法可应用于一般边界条件下圆柱壳结构自由振动特性分析。

在此基础上，计算另外三组边界条件(SS-F，SS-SD，SS-C)圆柱壳结构自由振动特性，为一般边界条件下圆柱壳结构自由振动特性分析提供数据积累(见表9)。

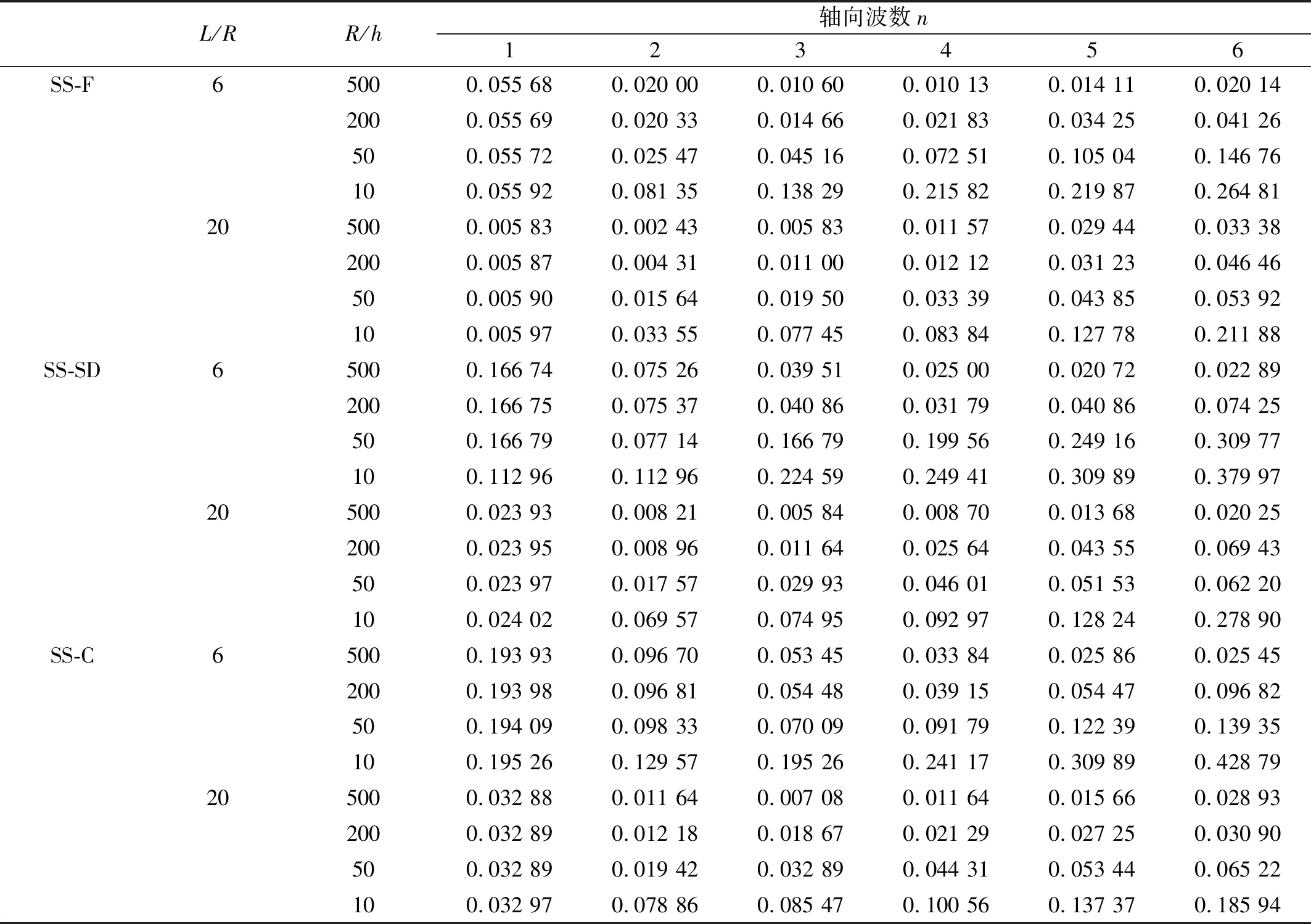
表9 SS-F，SS-SD，SS-C边界条件下圆柱壳结构频率参数ΩTab.9 The frequency parameters Ω under the boundary conditions of SS-F, SS-SD and SS-C

从表9可知，母线与半径长度比对计算结果影响较大，在相同半径长度与厚度比情况下，母线长度增大，结构的固有频率会随之增大。同理，在相同的母线长度与半径的长度比下，结构厚度增大，结构的固有频率也随之增大，但在不同轴向波数情况下，其增长率并不一致。

4 结 论

本文基于区域能量分解法，位移容许函数采用第一类正交切比雪夫多项式与三角级数表示，基于广义变分原理和最小二乘残差原理，建立了一般边界条件下圆柱壳结构自由振动分析模型，并对最小二乘残差加权系数与区域分段数对于数值计算的稳定性进行研究分析，在此基础上，从固有频率参数出发，对经典边界条件及一般弹性边界下圆柱壳结构自由振动特性进行了分析，验证了本文方法的有效性。为柱壳结构的前期快速设计提供一种可靠的手段。研究成果可为一般边界条件下圆柱壳结构自由振动特性分析提供数据积累和方法依据。