基于小波变换的非平稳排气噪声信号阶次分析方法
刘海涛
(华东交通大学 机电与车辆工程学院, 南昌 330013)
阶次噪声在汽车排气噪声中占居主要成分,对汽车声品质有着重要的影响,同时阶次成分的定量提取是排气消声结构分析设计的基础[1]。阶次分析方法主要分为硬件阶次跟踪法和计算阶次跟踪法(Computed Order Tracking, COT)[2],随着计算机技术的发展,计算阶次跟踪法逐渐成为主流[3]。计算阶次跟踪法都采用的是时域等间距的原始数字信号,经过多年发展已形成了多种处理方法。基于短时傅里叶变换的阶次分析方法由Gabor提出,可以对非稳态信号进行时(转速)-频表示,但是不能重构阶次分量的时域波形,无法定量计算阶次声压级,目前许多学者以短时傅里叶变换为基础,结合其它方法对旋转机械进行阶次追踪及运行状态的监测和诊断[4-5]。基于等角度重采样的阶次分析方法最早由Potter[6]提出,该方法对键相脉冲的正时精度非常敏感,转速曲线对于频谱精度也有影响。基于等角度重采样的阶次跟踪分析虽然能够进行时间(转速)-阶次表示,但是不能重构阶次分量的时域波形,主要用于轴承齿轮的故障识别[7-8]。Vold等[9]首次在Kalman滤波器的基础上提出了基于角速度的Vold-Kalman阶次跟踪算法,并后续对VKF进行理论改进,提出了基于角位移的Vold-Kalman阶次分量提取方法[10]。此阶次跟踪分析方法能够对转速变化进行自适应调整,避免了由于时频变换和重采样导致的相位偏移,可以实现阶次分量的时域波形重构,但是不能对信号进行时-频表示,同时需要进行大规模的解耦计算,较难实现在线处理[11]。Albright等[12]提出基于Gabor时频变换的阶次跟踪分析,随后Pan等[13]对该方法进行改进,使得该方法可以解决交叉阶次分离的问题。基于Gabor时频变换的阶次跟踪分析技术,即可对信号进行时-频表示,也可通过重构获得阶次分量的时域波形,从而更加全面地分析阶次噪声。但是这种方法经过时频变换后阶次分量在相位上有偏移,且该方法的时间窗的宽度与频率无关,是一种恒分辨率分析,因而对非平稳时变信号提取的阶次信号存在误差,限制了该方法的应用。
以上阶次分析技术都是以傅里叶变换为基础,而傅里叶变换为线性变换,是一种恒分辨率分析,需要进行信号重构获取阶次分量的时域波形,计算复杂,在线分析实时性较差[14]。加速行驶中的汽车排气噪声是非线性的时变信号,需要一种非线性可变分辨率的分析方法对其阶次噪声成分进行准确追踪提取。相对于傅里叶分析,小波变换提供了一种自适应的时域和频域同时局部细化的变换分析方法[15-16],通过伸缩和平移运算能对信号进行多分辨率细化分析。目前,也有学者采用小波变换进行阶次跟踪分析,但小波变换仅用来进行故障特征的分离,以提高故障诊断识别率[17-18]。本研究目标是准确获取排气噪声中准确的阶次成分时域波动信号,以便于进一步的声品质回放分析及汽车分类识别研究。因而本文拟构造标准的小波函数用于排气噪声中阶次时域信号的准确提取,简化阶次成分提取过程,形成标准的阶次定量分析方法,从而为排气声品质研究及车辆分类识别研究提供可靠的信号分析基础。
1 转速脉冲信号处理
对于旋转设备,阶次信号与转速直接相关,因而阶次分析首先需要获得准确的转速曲线。目前,转速测量装置获得的转速信号一般为脉冲信号,根据相邻脉冲之间的时间间隔及每转脉冲数即可计算转速,各脉冲区间的平均转速计算公式为
(1)
式中:n(t)为发动机转速;z为每转脉冲数;ΔT为相邻两个脉冲之间的时间间隔。
转速脉冲信号是由数据采集器等间距采样获取,设转速脉冲信号中出现的第i个脉冲在信号序列中的序号为sn(i) ,那么第i个脉冲和第i+1个脉冲之间的时间间隔为
ΔT(i)=[sn(i+1)-sn(i)]/fs
(2)
式中:fs为采样频率。联立式(1)和式(2)即可计算出各脉冲区间内的平均转速。而各转速点所对应的时间序列,可由式(3)求得。
tn=sn(i)/fs
(3)
根据式(3),即可求得转速曲线。但由于电气干扰,通过转速脉冲信号计算出的转速曲线一般会存在波动情况,因而需要对转速曲线进行平滑处理。三次样条曲线是分段三次多项式插值,能保证曲线上位置连续、斜率连续以及曲率连续变化,从而形成一条把所有主干点连接起来的平滑曲线。本文中采用三次样条曲线对转速曲线进行插值计算,从而获取光滑的转速曲线。
2 基于小波变换的时变信号阶次提取
小波变换是一种可变分辨率的分析方法,通过伸缩和平移运算能对信号进行细化分析。而运用小波分析进行阶次噪声提取,需要先构造小波函数。
2.1 基小波函数的构建
时变排气噪声信号的阶次提取,其实质是跟踪转速信号换算的阶次中心频率,进行时变带通滤波获取各阶次成分,因而先从带通滤波器出发构建基小波函数。实偶的理想带通传递函数为
(4)
式中:HB(f)为理想带通传递函数;FL为下限截止频率;FH为上限截止频率。理想带通滤波器的频域通带范围为[FL,FH],止带范围为[0,FL] 和[FH,+∞]。实际操作中,理想带通传递函数可以用两个理想低通传递函数之差获得,即
HB(f)=HLH(f)-HLL(f)
(5)
式中:HLH(f)为高频低通传递函数;HLL(f)为低频低通传递函数。
而理想低通传递函数的冲激响应函数是一个辛克函数,其表达式为
hL(t)=2Fcsinc(2Fct)
(6)
式中:hL(t)为理想低通冲激响应函数;Fc为低通截止频率。结合式(6),理想带通传递函数的冲激响应函数为
hB(t)=2FLHsinc(2FLHt)-2FLLsinc(2FLLt)
(7)
式中:FLH为理想带通传递函数上限截止频率;FLL为理想带通传递函数下限截止频率。理想带通传递函数以及理想带通冲激响应函数的波形,如图1所示。

(a)理想带通传递函数
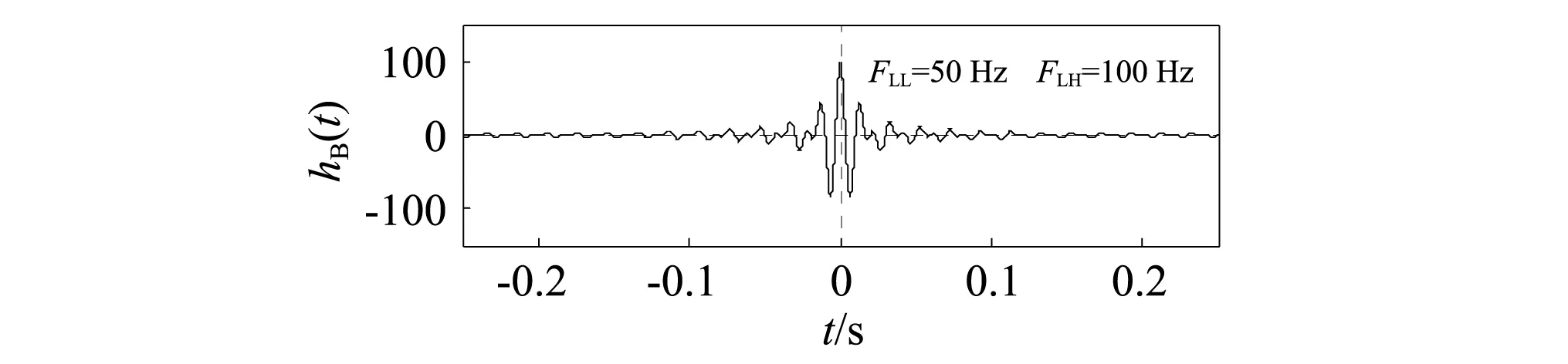
(b)理想带通冲激响应函数图1 理想带通传递函数及冲激响应函数曲线Fig.1 Ideal bandpass transfer function and impulse response function curve
然而进行时变信号中阶次成分的滤波处理时,需要通过带通传递函数中心频率的偏移以及带宽的伸缩实现信号多分辨率细化分析,即带通滤波器的中心频率及带宽需要跟随相关比对时间τ的变化而变化,其数学描述可用式(8)表示。
(8)
式中:wp(τ)为带通滤波器的带宽;fc(τ)为阶次中心频率;τ为相关比对时间系统。
带通滤波器带宽的选择决定了阶次提取的精度,需要根据实际研究对象的信号特征进行合理选取。同时带宽随相关比对时间系统而变化,从而实现信号的多分辨率细化分析。而各阶次中心频率由发动机的转速计算得出,如式(9)所示。
(9)
式中:ε为阶次数,一般发动机点火阶次及其倍频是声能量集中的地方。如对于四冲程四缸发动机,2阶、4阶、6阶、8阶是需要重点关注的阶次。
联立式(7)~式(9),可以得到的理想带通冲激响应函数的表达式
(10)
(11)
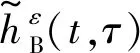
2.2 小波函数的截取分析
归一化的汉明窗函数的表达式为
(12)
式中:Wβ(t)为汉明窗函数;β为窗提升率,其值取β=0.54/0.46;Tw为截取的窗宽,其大小直接决定带通滤波器的过渡带宽BT,两者之间的关系为
(13)
为了验证施加汉明窗以后旁瓣的抑止效果,对式(7)中的理想带通冲激响应函数施加汉明窗进行截取。加窗带通冲激响应函数可以表示成窗函数与理想冲激响应函数之积,即
hwB(t)=Wβ(t)hB(t)
(14)
式中:hwB为加窗带通冲激响应函数,其形成过程可用图2表示。其中FLL=50 Hz ,FLH=100 Hz,Tw=0.2 s。

图2 汉明窗带通冲激响函数的形成Fig.2 The formation of the impulse response function of the Hamming window
为了查看加窗截取后的波动和畸变,对函数hwB(t)进行傅里叶变换,如式(15)所示。
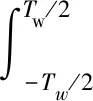
(15)

理想带通传递函数、汉明窗带通传递函数以及矩形窗带通传递函数的曲线,如图3所示。从图3(a)可以看出,加矩形窗的带通传递函数在过滤带有较大的波纹畸变,而加汉明窗实现了平稳过渡。为了显示更加清楚,将纵坐标采用对数显示,如图3(b)所示,加矩形窗的带通传递函数第一旁瓣的衰减量只有22 dB,而加汉明窗函数的第一旁瓣衰减达52 dB,说明汉明窗对带通传递函数的波纹畸变有非常好的抑制作用。因而本文中采用汉明窗函数对基小波进行截取,生成进行相关比对的小波函数,如式(16)所示。
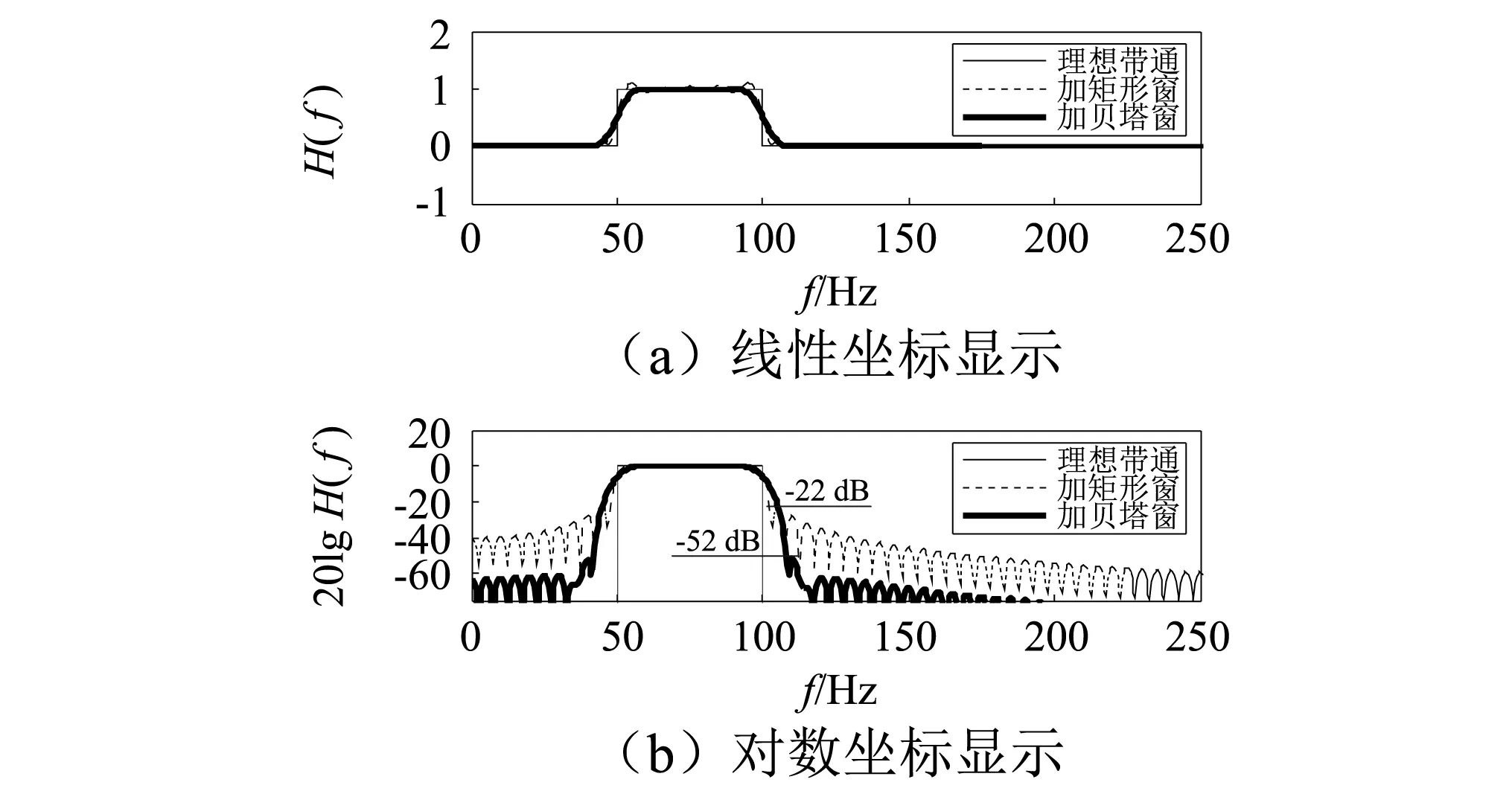
图3 加窗带通传递函数的频谱旁瓣抑制效果对比Fig.3 Sidelobe suppression effect comparison of windowed bandpass transfer function
(16)

2.3 时域信号相关变换
以上分析中获取了加窗小波函数,将其对时变噪声信号进行时域相关变换,即可获取各阶次的时域波动信号。
图4中:p(t)为指采集的噪声信号;pε(t)为指经过时域滤波系统以后的各阶次的时域波动信号。对于时域滤波系统,系统输出信号应该是加窗小波函数与输入信号之间的卷积
(17)
图4 加窗小波函数的时域滤波系统Fig.4 Time domain filtering system with windowed wavelet function
(18)
按式(18)进行比对变换计算即可提取各阶次的时域波动信号。
2.4 转速域阶次声压级的求取
时域波动信号不便于定量对比分析,需将时域阶次信号进行声压级变换,再通过转速曲线插值到转速域,从而为不同消声结构的阶次噪声定量比较提供方便。时变信号的有效声压计算公式为
(19)

声压级变换公式为
(20)
式中:Ls(τ)为时变声压信号的声压级;p0为参考声压,p0=2×10-5Pa。
3 信号采集
3.1 转速信号采集
汽车蓄电池的电压受发电机的影响会产生波动,发电机与发动机直接相连,故电池电压波动的频率与发动机转速正相关。因而可以从汽车点烟器获取波动的电压信号,再经信号调理获取转速脉冲信号。此方法在车内即可操作完成,且不受车辆振动的影响。测试装置示意图如图5所示。

图5 发动机转速测量装置示意图Fig.5 A schematic diagram of the engine speed measuring device
测试中的信号调理仪选用的是德国KMT公司生产的RPM-8000-PRO型汽车专用转速信号调理仪,可直接输出转速脉冲信号。某款1.5 L排量小汽车在二档全加速踏板加速工况下的采集的转速脉冲信号,如图6所示。
由图6可以看出,经过KMT转速仪的处理,所记录的转速脉冲信号由逻辑值0和1组成,单位时间内的脉冲数与转速相关。

图6 汽车发动机转速脉冲Fig.6 Engine speed pulse
3.2 加速工况下排气噪声信号采集
为了获取车辆实际加速工况下的排气辐射噪声信号,需要将传声器固定在汽车车身上,测试传感器安装示意图如图7所示。

图7 运动工况下尾管辐射噪声实车测试装置示意图Fig.7 Schematic diagram of a real vehicle testing device for tail radiated noise measuring under moving conditions
本文中采用某款1.5 L四缸发动机的汽车采集尾管辐射噪声,将传声器安装在车尾端的支架上,支架与车身焊接牢固。传声器与排气管出口的轴线在同一平面内,最低离地不能小于0.2 m。传声器与尾管口轴线的夹角为45°,距离为0.5 m。传声器头部安装有风罩,以消除运动起来以后风的影响。试验在干净平整的噪声测试道路上进行,运动工况为二档全加速踏板加速工况。图8显示了测试实物图,实车测试装备主要包括测试车辆、电脑、数据采集设备、传声器、转速表以及相应的线束。

图8 实车测试装置Fig.8 The real car test device
4 信号处理及分析
4.1 信号预处理结果
采集获得的转速脉冲信号以后,通过式(1)~式(3)即可计算出发动机的瞬时转速,如图9所示。

图9 脉冲信号计算的瞬时转速曲线Fig.9 Instantaneous speed curve calculated by pulse signal
由图9可以看出,在转速较高的区间,由于汽车上电器电信号的干扰,计算出的转速曲线会存在波动情况,因而对其进行三次样条曲线平滑处理,处理后的转速曲线如图10(a)所示。
采集的原始噪声信号ps(t)以及平滑后的转速n(t),如图10所示。
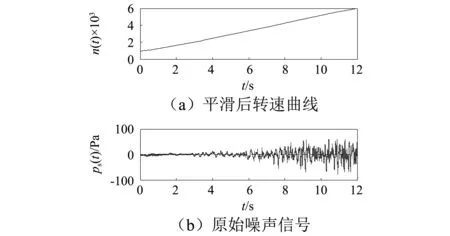
图10 原始排气辐射噪声信号及平滑转速曲线Fig.10 The original exhaust emission noise signal and smoothed speed curve
由图10(a)可以看出,尾管辐射噪声波形起伏较大,可能是由于车身和传感器支架的低频振动引入的干扰信号。因而需要先对原始信号进行高通滤波,滤除低频干扰信号。高通输出信号的滤波表达式如式(21)所示。

(21)
式中:hL(t)为理想低通冲激响应函数,其表达式如式(22)所示。
hL(t)=2FLsinc(2FLt)
(22)
式中:FL为低通截止频率,一般噪声信号取15 Hz即可。滤波前后的尾管辐射噪声信号如图11所示,可以看出高通滤波器滤除了原始信号中的低频波动成分。
对滤波后的尾管辐射噪声信号p(t)进行短时傅里叶变换,其表达式为

(23)
式中:Pr(f,τ)为相关频谱函数,可以绘制成三维色谱图,如图12所示。

图11 尾管辐射噪声高通滤波前后信号Fig.11 The radiated noise signal from the exhaust tail tube

图12 尾管辐射噪声信号色谱图Fig.12 The tail radiated noise signal chromatogram map
从图12中可以看出,尾管辐射噪声信号的阶次能量主要集中在2阶、4阶、6阶,即四缸机的点火频率及其倍频。图中黑色实线是跟据转速信号计算的4阶中心频率,刚好能与阶次线吻合。
4.2 排气噪声阶次分量的时域提取
从图12中可知,汽车加速情况下排气噪声中的阶次成分能量集中在较窄的频带,其带宽基本不随时间变化。因而对于排气噪声阶次成分的滤取,基小波函数中的带宽参数wp(τ)取常量即可。选取合理的参数,通过式(18)中的相关内积计算可获得各阶次成分的时域波动信号,如图13所示。

图13 排气辐射噪声各阶次成分时域波动信号Fig.13 The time domain fluctuation signal of exhaust radiated noise
从图13中各阶次时域波形中,可以清楚看出各阶次在各个时段的噪声信号波动情况。单独分离出来的各阶次时域信号可以直接在听音室进行独立播放,从而实现更加精准的声品质分析,比如各阶次信号单独评价、阶次组合评价,还可对阶次波形幅值进行修改,探索高声品质的阶次分量配比模式,从而为消声器的声学结构设计提供依据。
将提取的2阶、4阶、6阶三种阶次时域波动信号叠加在一起,其表达式为
pεa(t)=∑pεi(t) (i=2, 4, 6)
(24)
然后对pεa(t)按式(23)进行短时傅里叶变换,可得到各阶次的相关频谱函数,绘制成色谱图如图14所示。

图14 各阶次分量色谱图Fig.14 The order noise component chromatogram map
图14显示了叠加的各阶次时域波动信号的色谱图,图中仅有2阶、4阶、6阶三种阶次信号,其它的无关噪声信号全部得到滤除。结合图12、图13及图14可知,按本文提出的基于小波变换的阶次分析方法成功准确提取了排气辐射噪声中的各阶次成分。
4.3 转速域阶次声压级的求取
根据式(19)和式(20)即可获得尾管辐射噪声总声压级以及各阶次成分的声压级曲线,如图15所示。
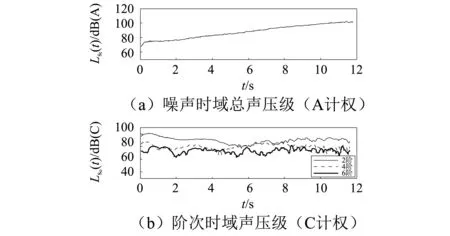
图15 时域总声压级及阶次声压级曲线Fig.15 Time domain total sound pressure level and order sound pressure level curve
从图15可以看出,经声压级变换之后,噪声信号变为声压级曲线,便于对噪声能量的大小进行量化对比分析。
尾管辐射噪声是时变信号,与发动机转速密切相关。将时域曲线变换到转速域,可以更加清楚的显示排气系统阶次消声性能与发动机转速之间的关系。通过平滑后的转速曲线,将声压级曲线的离散的时间序列{tk}代入转速线性函数中,即可得到离散的转速序列{nk},从而实现时域向转速域的变换。按此方法将图15中的曲线变换到转速域,转速域的尾管辐射噪声总声压级Lst(n)和阶次声压级Lso(n)如图16所示。

图16 转速域总声压级及阶次声压级曲线Fig.16 The total sound pressure level and the order sound pressure level curve in the rotational speed domain
从图16中转速域声压级曲线,可以直观的定量分析各转速段噪声相的大小。比如尾管辐射噪声中的4阶线,在1 000~ 1 200 r/min,1 700~2 300 r/min以及3 500~4 500 r/min的转速段都有明显的峰值,是阶次噪声控制中需要重点关注的转速带。因而基于小波变换的尾管辐射噪声阶次成分定量提取方法,为汽车排气噪声的特征分析提供了理论基础和技术手段。
5 结 论
本文从小波变换思路出发,通过理想带通传递函数构建基小波函数,通过中心频率、带宽以及相关比对时间三个参数来控制基小波函数的平移和伸缩,实现局部细化分析;探索小波函数的截取方式对频谱泄漏的影响,选取合适的窗函数截取小波函数,并通过与时域噪声信号的相关比对准确提取各阶次成分的时域信号;通过实车测试获取加速工况下的排气辐射噪声信号,采用构建的小波函数进行阶次提取。实测信号分析结果表明,本文提出的分析方法可准确提取出非平稳排气噪声中的阶次成分。本文研究主要得到以下结论:
(1)提出一种基于小波变换的非线性多分辨率的细化阶次分析计算方法,能够准确提取出非平稳排气噪声中阶次成分的时域波动信号,计算方便快捷。
(2)采用汉明窗截取基小波函数,可以有效抑制过滤带的波纹畸变,极大衰减第一旁瓣衰减,减少频谱泄漏所带来的误差。
(3)通过理想带通冲激响应函数构建的用于阶次成分提取的标准基小波函数,为排气声品质研究及车辆分类识别研究提供可靠的信号分析基础。

