单自由度含对称约束碰振系统周期运动的转迁规律分析
李得洋, 丁旺才, 丁 杰, 李 飞
(1.兰州交通大学 机电工程学院,兰州 730070; 2.天津铁道职业技术学院,天津 300010)
由于制造工艺、机械零部件之间的热胀冷缩等因素的影响,在实际工程力学系统中存在大量的非光滑因素,如列车车轮与钢轨的碰撞、飞船对接引起的碰撞[1]等。近年来国内外学者对含非光滑因素的动力学系统展开了广泛的研究[2],通过建立不同的模型,利用理论分析和数值试验验证逐步揭示了非光滑系统的动力学特性。Shaw等[3]采用接缝法精确地求解了分段线性振子的动力学响应,并通过复合的全局映射研究了系统周期响应的稳定性问题。Bernardo等[4]系统研究了分段光滑系统的擦边流,得到了擦边分岔的规范型映射。Kundu等[5]构建了四种单自由度弹性约束系统Grazing分岔的范式映射,并研究了擦碰轨道邻域内Poincaré映射的特性。徐慧东等[6]研究了一类单自由度分段线性非光滑系统周期运动的分岔现象和混沌行为。张惠等[7]研究了含间隙和预紧弹簧碰撞振动系统由于擦边引起不动点处Jacobian矩阵的行列式和迹的变化特性。吴志强等[8]利用平均法和约束分岔理论分析了一类含非连续阻尼的单自由度分段线性系统参数对系统振动性能的影响。汪诤等[9]应用等效模拟电子电路高效快速的对对称间隙单自由度振动系统进行了数值仿真,为非线性系统的仿真和试验提供了一种参考。
胞映射方法最先由Hsu[10]在20世纪80年代初提出,随后Levitas等[11-12]基于胞映射的思想发展出庞加莱型的简单胞映射法,这种方法是在状态空间的定相位面中形成胞空间,并通过在此空间中运用简单胞映射方法对原动力系统进行研究。本文利用庞加莱型的简单胞映射法对系统周期共存现象进行分析。李健等[13]根据非光滑动力学系统特点,得到了非光滑系统吸引子和吸引域的胞映射计算方法,并在一类单自由度碰振系统上验证了方法的有效性。Chong等[14]利用数值方法对简谐激励下含间隙碰撞振动系统在分岔点附近周期共存现象进行了研究。田亚平等[15]采用PNF(Poincaré-Newton-Floquet)法和延续追踪法研究了三自由度单级齿轮传动系统在多参平面内的分岔、冲击特性随参数转迁和参数间的耦合关系。
近年来学者们大多都是基于单个参数变化下对系统的动力学特性进行研究。为更全面地分析非光滑系统的全局动力学特性,本文在多个参数协同变化下进行数值仿真,同时结合胞映射方法分析了一类单自由度含对称弹性约束碰撞振动系统在不同参数域内经各种非光滑分岔进行转迁的规律。
1 系统的力学模型及运动微分方程
图1所示为单自由度含对称弹性约束碰撞振动系统模型,质量为M的振子由刚度为K1的线性弹簧和阻尼系数为C的线性阻尼器相连接,并在简谐激振力F0sin(ΩT+τ)的作用下沿水平方向振动。以系统的静平衡位置为空间坐标的原点建立坐标系,振子M的位移为X,在振子M的两侧距离为B的位置固定两个刚度为K2的弹性约束。在简谐激励的作用下,当振子的位移较小时,系统为单自由度的线性振动系统;而当振子的位移小于-B或大于B时,振子会与左右两侧的弹性约束接触在一起振动,由于间隙的存在和碰撞的产生,系统会表现出强非线性和非光滑的特性。

图1 单自由度含对称弹性约束碰撞振动系统模型Fig.1 The model of a single-degree-of-freedom vibro-impact system with symmetrical soft constraints
系统无量纲运动微分方程为
(1)

方程的通解为
(2)

2 系统n-1-1S周期运动的周期解


为便于周期运动推导,引入下列符号
则系统n-1-1S周期运动的周期解可表示为
(3)

将t=0及t=t1+代入式(3),可得积分常数关于初始条件的表达式
j1=Φ1(0)-1(z(0)-M1(0)CS-Q)j2=Φ2(0)-1(z(t1)-M2(0)NCS)
(4)
将j1,j2代入式(3)有
(5)

(6)
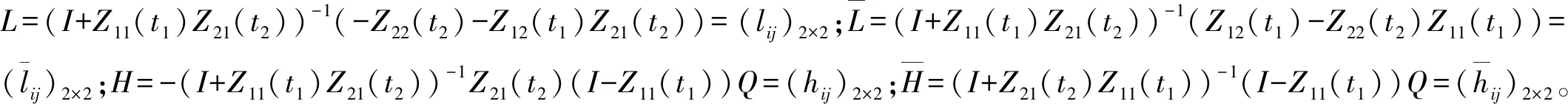
由初始条件x(0)=b和x(t1+)=b可得初相位
(7)
(8)
根据初相位的表达式,可以得到n-1-1S周期运动存在必须要满足的必要条件:



(9)
通过数值方法可获得方程的根t1,进而确定系统n-1-1S周期运动的周期解。
3 系统Poincare映射的建立及稳定性分析
为了研究系统周期运动的稳定性、存在区域以及局部分岔问题,建立三个Poincaré映射选择定相位面可以统计出系统周期运动的周期数;选择碰撞面可以统计出振子与左右约束面的碰撞次数。根据金栋平等研究中的方法选择碰撞面Σp+构造系统Poincaré映射——p∶Σp+→Σp+,则通过Poincaré映射的Jacobi矩阵在不动点处的特征值来研究系统n-p-q运动的稳定性及分岔类型。
4 不同参数域内相邻周期运动转迁规律分析
将系统参数间隙b和激励频率ω作为研究对象。为研究系统周期运动类型和转迁规律的多样性,取系统参数(1):ξ=0.2,μk=100,b∈[0.1,3]和ω∈[0.1,2]。系统在(ω,b)参数平面内周期运动分布图,如图2所示。图中用不同深浅的颜色及相应的符号表示各类

图2 在(ω,b)参数平面内系统周期运动分布图Fig.2 The distribution diagram of periodic motions in the (ω,b)-parameter plane for the system

根据系统周期运动分布及转迁规律的不同,将图2(a)所示的参数平面划分为两个区域:ω∈[0.1,2],b∈[0.1,0.556]区域为参数域Ⅰ;ω∈[0.1,2],b∈[0.556,3]区域为参数域Ⅱ,在b>1.2的区域,系统主要存在1-0-0S,1-1-0,1-0-1和1-1-1S周期运动。1-0-0S与1-1-1S之间主要通过擦边和鞍结分岔相互转迁,1-0-0S与1-1-0,1-0-1周期运动之间主要通过擦边分岔相互转迁。
4.1 参数域Ⅰ内相邻周期运动转迁规律分析
在参数域Ⅰ内,系统在高频区主要以1-1-1S和1-1-1AS周期运动为主;随着ω的减小,1-p-pS和1-(p+1)-(p+1)S周期运动被一些具有相似转迁规律的过渡区隔开,过渡区内各周期运动之间的转迁规律为:在ω从大到小的过程中,1-p-pS周期运动经叉式分岔转迁为1-p-pAS周期运动;在经历若干个倍周期分岔序列(如1-(p+1)-p和1-p-(p+1)倍周期分岔序列等)后从最后一个倍周期分岔序列的混沌运动中退化出1-(p+1)-(p+1)S周期运动。在ω从小到大的过程中,1-(p+1)-(p+1)S周期运动经鞍结分岔进入混沌;在经历若干个逆倍周期分岔序列后从最后一个逆倍周期分岔序列中退化出1-(p+1)-p或1-p-(p+1)周期运动,然后经鞍结分岔转迁成两种反对称1-p-qAS的周期运动,最后经逆叉式分岔转迁为1-p-pS周期运动。过渡区内系统主要通过鞍结、叉式和倍周期分岔进行周期运动之间的转迁,系统周期运动的类型丰富,且在周期运动之间还夹杂着若干混沌带,所以称此区域为“周期夹杂区”。这些周期夹杂区区域大小随着ω的减小会缩小,其左侧边界线由1-(p+1)-(p+1)S周期运动的鞍结分岔点组成,右侧边界线由1-p-pS周期运动的叉式分岔点组成。
由于参数域Ⅰ内各周期运动对应的参数区域随着间隙的增大而逐渐减小,故取小间隙b=0.1时以位于1-1-1S周期运动与1-2-2S周期运动之间的周期夹杂区为例来具体分析上述的转迁过程,系统在定相位面Σn上的分叉图如图3所示,图中用不同深浅颜色来表示不同吸引子,从而可方便观察不同参数处吸引子共存现象。在ω从大到小的过程中,1-1-1S周期运动经叉式分岔转迁为两个反对称的1-1-1AS周期运动(将一个周期运动绕原点旋转180°后,它会和另一周期运动的相图完全重合);随后系统经1-1-1AS周期运动的倍化序列通向混沌运动;随着ω的减小系统经若干个倍周期分岔序列后由混沌退化出1-2-2S周期运动。在ω从小到大的过程中,1-2-2S周期运动首先经鞍结分岔进入混沌;在经历若干个逆倍周期分岔序列后经最后一个逆倍周期分岔序列产生1-2-1或1-1-2周期运动;在ω=2.362 337 7处不动点对应的两个特征值为:λ1=1.000 263 639 007 594,λ2=0.345 025 671 782 827。

图3 b=0.1时系统局部分叉图Fig.3 Local bifurcation diagrams of the system for b=0.1
此时系统发生鞍结分岔,1-2-1或1-1-2周期运动转迁为两种反对称1-1-1AS周期运动,最后1-1-1AS周期运动经逆叉式分岔转迁为1-1-1S周期运动。

结合分岔图和通过胞映射所得到的吸引域分布图可以得出:1-1-1S周期运动转迁到1-2-2S周期运动要经历凸起的周期夹杂区;由于叉式和鞍结分岔的存在使得周期夹杂区内存在丰富的吸引子共存现象;其左侧边界线由1-2-2S周期运动的鞍结分岔点组成,右侧边界线由1-1-1S周期运动的叉式分岔点组成。

图4 b=0.1时定相位面Σn上的吸引域Fig.4 The attractor and its attracting domain on fixed phase Σn for b=0.1
4.2 参数域Ⅱ内周期运动转迁规律分析
由于此系统的对称性,叉式分岔和逆叉式分岔为其特有的分岔类型,擦边分岔与此两种分岔发生的次序不同将会导致1-p-pS与1-(p+1)-(p+1)S周期运动之间的相互转迁变得复杂。以叉式分岔和逆叉式分岔为参考基准,如果擦边分岔发生在叉式分岔和逆叉式分岔之间,擦边分岔将导致1-(p+1)-(p+1)AS与1-(p+1)-p或1-p-(p+1)之间的相互转迁(以b=0.825 5为例分析);如果擦边分岔发生在叉式分岔和逆叉式分岔之后,擦边分岔将导致1-(p+1)-(p+1)S与1-p-pS之间的相互转迁(以b=0.764 8为例分析);倍周期分岔如果发生在叉式分岔后,擦边分岔在此过程中将会导致混沌运动与3-(3p+1)-(3p+1)S周期运动、混沌运动与1-p-pS周期运动之间的相互转迁(以b=0.700 5为例分析)。
当不出现叉式分岔时,由于擦边分岔和鞍结分岔的不可逆,将会导致在1-p-pS与1-(p+1)-(p+1)S周期运动之间存在多态共存区(以b=0.6为例分析)。
结合系统在碰撞面Σp+上的单参分岔图和图2所示的周期运动分布图对以上参数所代表的系统转迁规律进行详细的分析(颜色较浅表示ω从大到小变化时得到的分岔曲线,颜色较深表示ω从小到大变化时得到的分岔曲线)。
(1)取b=0.6时系统的单参分岔图(见图5)并结合图2(a)有:
①随着ω的减小,在ω=0.598 26时系统出现1-1-1S擦边运动(如图6所示,虚线表示弹性约束的位置,论文后面相图中的情况和此处一致),由于擦边分岔的奇异性导致振子与两侧约束面碰撞次数同时加一,而周期数不变,1-1-1S周期运动转迁为1-2-2S。同理,在ω逐渐减小的过程中会有一系列的1-p-pS周期运动通过擦边分岔转迁为1-(p+1)-(p+1)S周期运动,并且1-(p+1)-(p+1)S周期运动对应的参数域逐渐变窄,当p足够大时,系统表现为Chatting-impact动力学特性。所以随着ω的逐渐减小,在参数域Ⅱ内存在如下的周期运动转迁规律

图5 b=0.6时系统单参分岔图Fig.5 The single-parameter bifurcation diagram of the system for b=0.6
②随着ω的增加,在ω=0.636 812 12处不动点对应的两个特征值为
λ1=1.000 622 463 428,λ2=0.019 303 201 837。
此时系统发生鞍结分岔,由此导致振子与两侧约束面碰撞次数同时减一,1-2-2S周期运动转迁为1-1-1S周期运动。所以在参数域Ⅱ内随着的逐渐变大存在如下的周期运动转迁规律
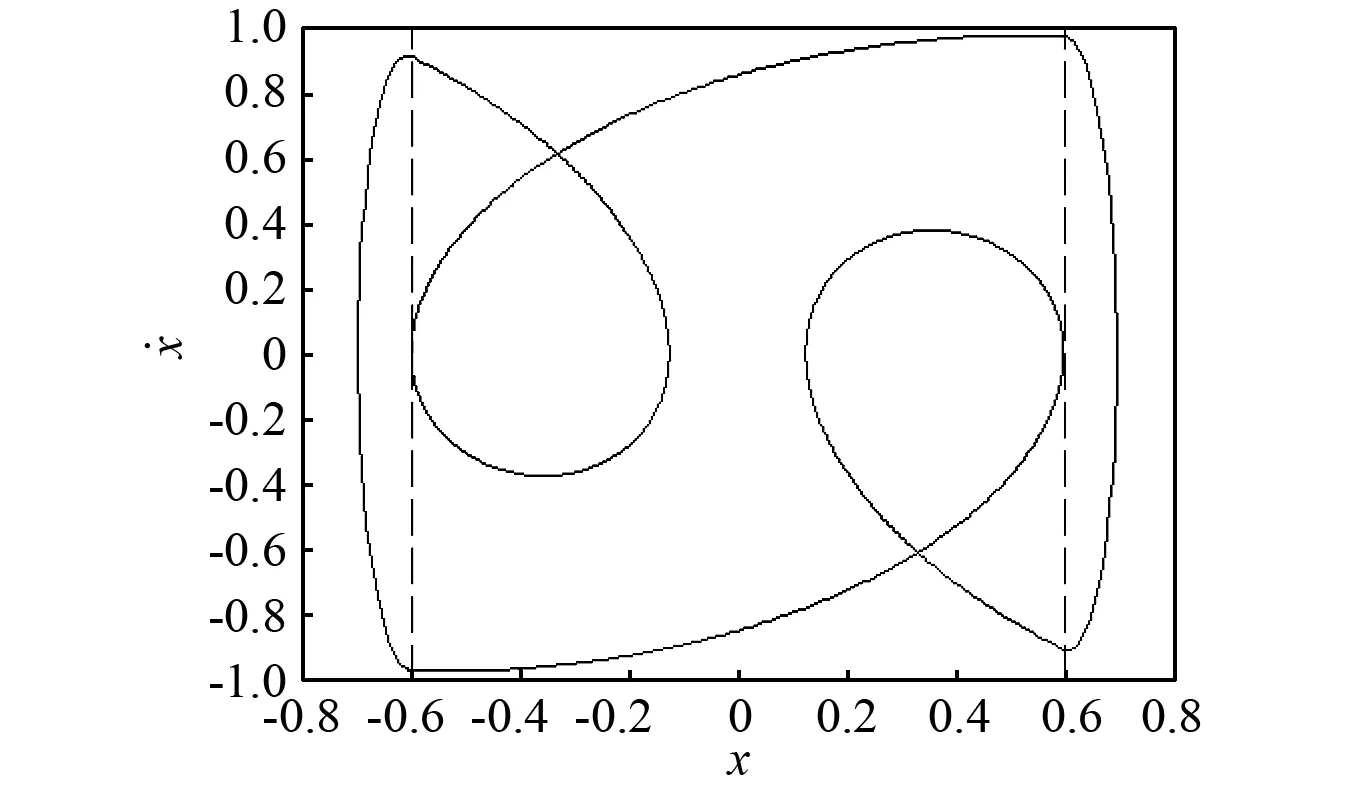
图6 振子1-1-1S擦边运动的相图Fig.6 Phase plane of 1-1-1S grazing motion


图7 b=0.6时定相位面Σn上的吸引域Fig.7 The attractor and its attracting domain on fixed phase Σn for b=0.6
通过以上分析可以总结出:在参数域Ⅱ内1-p-pS与1-(p+1)-(p+1)S周期运动在相互转迁的过程中会经历1-p-pS与1-(p+1)-(p+1)S周期运动共存的过渡区,导致转迁过程不可逆。由于此过渡区内仅仅共存有相互转迁的这两个周期运动,与前面定义的周期夹杂区在共存周期运动的个数和转迁的过程上有明显的区别,所以将此区域定义为“多态共存区”。此区域的左侧边界线由1-p-pS周期运动的擦边分岔点组成,右侧边界线由1-(p+1)-(p+1)S周期运动的鞍结分岔点组成。
(2)当b=0.825 5,b=0.764 8和b=0.700 5时,系统的单参分岔图如图8所示,结合图2(b)~图2(d)可以观察到:在每个1-p-pS周期运动擦边分岔的边界处分布着具有相似转迁规律的过渡区。
过渡区内都存在以下两条基本的转迁规律


图8 系统的单参分岔图Fig.8 The single-parameter bifurcation diagram of the system



图9 周期运动的相图图9 Phase plane portraits of periodic motions

图10 b=0.700 5时Σn截面上的吸引域Fig.10 The attractor and its attracting domain of periodic motion of the system for b=0.700 5

通过以上的分析可得出:由于擦边、叉式和倍周期分岔的同时存在以及产生顺序不同导致1-p-pS与1-(p+1)-(p+1)S周期运动在转迁的过程中有过渡区的存在;对称周期运动之间、非对称周期运动之间、混沌运动与3-(3p+1)-(3p+1)S周期运动、混沌运动与1-p-pS周期运动之间通过擦边分岔相互转迁。此区域的左侧边界线由1-(p+1)-(p+1)S周期运动的叉式分岔点组成,右侧边界线由1-p-pS周期运动的擦边分岔点组成。
5 结 论
本文以单自由度含对称弹性约束碰撞振动系统为研究对象,根据系统周期运动的边界条件和衔接条件确定了n-1-1S周期运动的周期解;在参数ω和b协同变化下进行数值仿真,同时结合庞加莱型胞映射方法详细分析了系统的周期运动转迁规律和全局动力学行为。
(1) 在ω∈[0.1,2],b∈[0.1,0.556]的参数域Ⅰ内,系统在高频区主要以1-1-1S和1-1-1AS周期运动为主;1-p-pS和1-(p+1)-(p+1)S周期运动之间的周期夹杂区具有相似的周期转迁规律:1-p-pS与1-p-pAS周期运动通过叉式分岔转迁;1-p-pAS,1-(p+1)-p,1-p-(p+1)周期运动经倍周期分岔进入混沌;1-(p+1)-p或1-p-(p+1)周期运动经鞍结分岔转迁为1-p-pAS周期运动;混沌运动退化为1-(p+1)-(p+1)S周期运动。共存的周期吸引子主要有:两个反对称的2i-2ip-2ipAS周期运动、2i-2i(p+1)-2ip与2i-2ip-2i(p+1)(i=0,1,2,…)周期运动以及1-(p+1)-(p+1)S周期运动与混沌等。
(2) 在ω∈[0.1,2],b∈[0.556,3]的参数域Ⅱ内:① 1-p-pS在周期运动发生擦边分岔的边界处分布着具有相似转迁规律的过渡区,过渡区内的转迁过程主要有:1-(p+1)-(p+1)S周期运动经叉式分岔转迁为1-(p+1)-(p+1)AS周期运动;1-(p+1)-(p+1)S周期运动与1-p-pS周期运动之间通过擦边分岔相互转迁;1-(p+1)-(p+1)AS与1-(p+1)-p,1-p-(p+1)周期运动之间通过擦边分岔相互转迁;混沌运动与3-(3p+1)-(3p+1)S周期运动、混沌运动与1-p-pS周期运动之间通过擦边分岔相互转迁;② 在有多态共存区的区域,由擦边和鞍结分岔完成1-p-pS与1-(p+1)-(p+1)S周期运动之间相互转迁,由于擦边分岔和鞍结分岔的分岔点不在同一位置,使得系统在这两个分岔点之间的参数区域共同存在两个稳定的1-p-pS与1-(p+1)-(p+1)S周期运动。

