基于频率-波数分析的激光Lamb波传播特性试验研究
刘增华, 冯雪健, 任 捷, 王双全, 何存富 ,吴 斌
(1. 北京工业大学 机械工程与应用电子技术学院,北京 100124;2. 北京工业大学 北京市精密测控与仪器工程技术研究中心,北京 100124)
金属板状结构在航空工业和舰船工业等领域有着大量的应用[1-2],其健康状况关系到整个部件以及整个设备的完整性,安全性和使用寿命,因此开展金属板状结构缺陷检测研究具有重要的应用潜力和科研意义。Lamb波因其传播距离较远、衰减小和对不同类型的缺陷均具有合理灵敏度等特点,在板类结构无损检测和结构健康监测方面展现出了巨大的应用潜力[3-5]。分析Lamb波在波导结构中传播时信号特征的变化是Lamb波检测技术的基本思想,通常采用一对传感器即可完成Lamb波信号的激励和接收[6]。为了获取更多的缺陷信息,提高缺陷检测精度,基于传感器阵列的Lamb波检测技术已被国内外众多学者广泛研究和发展[7-12]。取得的研究成果表明该技术可有效地实现缺陷的识别和定位,但在缺陷定量检测方面仍存在较多挑战[13]。主要包括:①传感器阵列和缺陷之间的相对位置会影响缺陷的检测能力;②由于Lamb波的频散和多模态特性,接收信号复杂难以分析,使得不易在时域或频域内有效地提取Lamb波信号中的缺陷信息;③接收信号中包含的缺陷信息和缺陷尺寸之间的定量关系往往不明确,给缺陷的定量造成一定困难。
各种类型的传感器,如压电传感器、电磁声传感器、空耦传感器、光纤传感器,激光传感器,已用于Lamb波信号的激励或接收[14-19]。近年来,随着激光超声检测设备的长足发展,以激光多普勒测振仪(Laser Doppler Vibrometer)和双波混频干涉仪(Two-wave Mixing Interferometer)为代表的激光超声检测设备被广泛用于Lamb波波场的采集[20-21]。利用激光以一定步长在空间上密集扫描接收Lamb波信号可获得整个扫描区域中的波场数据。通过一帧一帧的回放可直观地看到不同时刻下Lamb波与结构特征或损伤之间的相互作用过程[22]。
波场数据中包含了丰富的缺陷信息,为弥补阵列检测技术在缺陷定量检测方面的不足,各类波场分析方法被广泛研究和发展。一些学者相继提出先采用阵列检测方法确定缺陷的位置,再利用波场分析等技术对缺陷进行定量表征[23]。Mallet等[24]采用压电激励、激光扫描接收的方式获得缺陷铝板上的波场信号,以接收信号幅值的包络用于缺陷成像。Köhler等[25]采用压电激励、激光扫描接收的方式获得波场信号,分别以强度和快照的形式实现了声场的可视化。Lee等[26-27]采用脉冲激光扫描激励、压电接收的方式获得复合材料板中的波场信号。利用相邻信号相减算法削弱波场中的入射信号,保留由缺陷引起的异常信号,最后利用整个信号长度内的最大峰峰值对缺陷进行成像。在此基础上,针对复合材料机翼铆钉处的脱粘缺陷,融合波数域滤波算法提取并保留波场信号中由脱粘引起的信息,最终利用能量法实现了脱粘成像。
上述研究成果中主要是对波场数据直接运用能量法对缺陷成像,或者是先对信号进行预处理然后运用能量法进行缺陷成像。值得注意的是,上述方法虽可用于缺陷大小的评估,但对于缺陷深度的评估尚显不足。缺陷会引起板厚的变化,对于特定模态和中心频率下的Lamb波信号在经过缺陷时则体现为波数的改变。为了获取与缺陷有关的波数信息,基于多维傅里叶变换的分析技术被发展用于缺陷定量评估。Ruzzene[28]利用压电激励,激光空间二维扫描接收的方式获取空间波场信号。最终,利用空间-波数滤波器提取出波场信号中微弱的缺陷信息,识别出铝板中的裂纹。Park等[29]采用全激光激励接收的方式获取空间波场信号,构造空间-波数滤波器提取波场中的驻波成分,实现了复合材料板中分层和脱粘缺陷的定位。Yu等[30]在铝板中采用压电激励,激光空间一维扫描接收的方式,获取时间-空间波场。通过二维傅里叶变换将信号从时间-空间域转换到频率-波数域,识别出了其中包含的模态成分。最后,采用短空间二维傅里叶变换方法得到波数在扫描路径上的分布情况,确定出通槽在扫描路径上所处的位置。Kudela等[31]采用压电激励,激光在空间二维扫描接收的方式,获取空间波场信号,采用波数滤波算法克服边界反射信号的影响,实现了铝板中裂纹尺寸和方向的评估。Rogge等[32]利用局部波数估计算法实现了复合材料板中分层缺陷的定量检测,并利用仿真数据研究了局部波数估计算法的适用范围。Flynn等[33]采用全激光激励接收的方式获取空间波场信号,利用局部波数估计算法分别实现了铝板、钢管以及复合材料机翼上厚度减薄区域的轮廓重构。朱倩等[34]采用了一种波数滤波损伤成像算法,对不同时刻的波场进行波数分析,根据不同波数所占的权值不同,采用波数域内加窗的方法滤除健康信号,并通过二维能量图实现了双层层压板中凹槽缺陷的定位成像。顾林霞[35]建立了缺陷铝板的三维有限元模型,得到仿真信号,采用局部波数估计的算法实现了不同形状和深度缺陷的定量评估。
近年来,基于频率-波数分析的缺陷检测算法主要为局部波数估计算法和波数滤波算法被广泛发展。研究的方向主要是针对不同类型的缺陷和损伤程度进行定量评估,评价上述两类算法的检测能力和精度,而对于算法本身没有更进一步的发展[36-37]。在Lamb波信号处理方面,在频率-波数域内进行滤波实现模态分离,获得较为纯净模态的波场信号[38]。此外,Ianni等[39]为了减少波场信号采集时间,提高检测效率,发展了基于压缩感知的波场重构技术。刘增华等[40]采用全激光激励接收的方式获取时间-空间波场信号,通过二维傅里叶变换将激光Lamb波信号从时间-空间域转换到频率-波数域,识别出激光Lamb波信号中包含的模态。
根据上述国内外研究现状可知,基于波数分析算法,非接触缺陷定量检测的研究还相对较少。基于此,本文采用全光学型激光超声激励接收系统,获取激光Lamb波时间-空间波场信号。通过二维傅里叶变换对该波场信号中包含的模态成分进行分析。为了保留在二维傅里叶变换中丢失的空间信息,借鉴短时傅里叶变换的思想,采用短空间二维傅里叶变换的方法得到信号的幅值-空间-波数表示。根据幅值-空间-波数谱可直观看出波数在扫描路径上的变化情况,据此可判别缺陷在扫描路径上的位置。最后,利用带通滤波结合连续小波变换的方法对幅值-空间-波数谱进行了优化。优化后的幅值-空间-波数谱只存在理论上应出现的波数成分,只有少量的干扰存在,与文献中采用压电激励激光接收得到的试验结果较为一致。
1 理论基础
时间和空间在傅里叶变换以后分别对应频率和波数,频率-波数曲线作为Lamb波频散特性的表现形式之一,为频率-波数域内研究Lamb波传播特性奠定了理论基础。
1.1 二维傅里叶变换
在空间上以步长Δx为间隔一维扫描接收M组Lamb波信号,每组采样点数为N,可得到一个M×N的时间-空间波场矩阵u(x,t)。类似于一维傅里叶变换,通过二维傅里叶变换将u(x,t)变换到频率-波数域内,得到频率-波数矩阵U(k,ω)为
(1)
式中:x为激励接收传感器之间的距离;t为信号接收的时长;ω为角频率;k为波数。以沿x正方向传播的信号为例,频率f0=150 kHz,波数k0=0.5 rad/mm,表达式为
u0(x,t)=sin(2π·150 000t-0.5x)
(2)
该表达式对应的时间-空间波场如图1(a)所示。将该时间-空间波场信号按照式(1)做二维傅里叶变换可得频率-波数谱,如图1(b)所示。从图1(b)中可以看出,该频率-波数谱的峰值位于坐标(f0,k0)处,对应波场信号中包含的频率成分和波数成分,据此可用于识别波场信号中包含的模态成分。频率-波数谱中峰值周围的成分是傅里叶变换能量泄漏的结果。
1.2 空间-频率-波数分析
通过二维傅里叶变换将u(x,t)从时间-空间域变换到频率-波数域,可揭示在时间-空间域内无法直接观察到的Lamb波传播特性。但由于二维傅里叶变换丢失了时间和空间信息,因此根据某一中心频率下的幅值-波数分布无法得知波数随空间位置的变化情况。为此,借鉴短时傅里叶变换的思想,采用短空间二维傅里叶变换保留空间信息,得到某一中心频率下的幅值-空间-波数谱。短空间二维傅里叶变换表达式为

图1 仿真波场信号频率-波数分析Fig.1 Frequency-wavenumber analysis of simulated wavefield signals

(3)
式中:xi为空间位置索引;W为空间窗函数。当|x|≤Dx/2时W的表达式为
(4)
式中:Dx为空间上窗的宽度。当|x|>Dx/2时,W(t,x)=0。
图2为空间-频率-波数分析的流程图,共分为四步:①确定二维窗函数的类型和宽度;②将二维窗函数的起始位置和时间-空间波场矩阵的起始位置对齐后相乘,完成截取;③对截取后得到的时间-空间波场矩阵做二维傅里叶变换,在得到的结果中选择某一中心频率下的幅值-波数谱作为当前窗函数所在位置的波数分布;④按固定步长移动窗函数至下一个位置,重复步骤②~步骤③,直到完成对全部波场信号的截取和变换。根据扫描路径上波数随空间位置的变化情况,可以确定缺陷在扫描路径上的具体位置。
1.3 连续小波变换
点光源激励出的激光Lamb波信号具有宽频和多模态的特点[41],采用连续小波变换提取特定中心频率信号,便于缺陷识别。对于任意平方可积的函数f(t)(即f(t)∈L2(R))的连续小波变换为
(5)
式中:t为时间;R为实数集;L2(R)为平方可积函数集;ψ(t)为一个基本小波或母小波。将母小波ψ(t)经伸缩和平移后可得小波序列
(6)
式中:a为伸缩因子;b为平移因子。

图2 空间-频率-波数分析的流程图Fig.2 Flow diagram of space-frequency-wavenumber analysis
2 试验装置
全光学型激光超声检测系统由激励单元、接收单元和扫描单元组成,如图3所示。在激励方面,激光控制器向Nd: YAG脉冲激光器提供能量使其内部晶体发生能级跃迁产生脉冲激光,经激光激励探头发出并作用在铝板表面。同时,激光控制器向示波器提供同步触发信号保证激光超声信号的同步激励接收。在接收方面,由连续光纤激光器输出连续激光,经分光器后分成两束。一束作为参考光直接输入到解调器,另一束经激光接收探头照射到铝板表面,然后将经铝板表面反射后携带了超声信号的激光(信号光)再经激光接收探头接收并输入到解调器中。在解调器中利用参考光和信号光将超声信号解调出来,最后由示波器接收显示。激光接收探头安装在二维扫描架上,由计算机控制可实现探头位置的精确移动和定位。为避免热弹机制产生的空气冲击波对接收信号产生影响,将激励和接收探头分置铝板两侧。
系统采用的Nd: YAG脉冲激光器在工作状态下产生的激光波长为1 064 nm,有效持续时间10 ns,激光单脉冲能量0~50 mJ,聚焦时光斑直径约为1.2 mm。通过激光控制器可实现激光单脉冲能量的调节和激发方式的选择。激光超声接收采用美国IOS公司双波混频干涉仪AIR-1550-TWM,连续激光波长为1 550 nm,光斑半径最小可达200 μm,检测带宽125 MHz。试验中,为保证激光是在热弹机制下激发超声信号,避免对铝板表面造成损伤,激光单脉冲能量设为10 mJ。为了提高信噪比,保持激光激励和接收光束与铝板垂直,并在待检测区域粘贴反光胶带(3M公司生产,型号8850,约0.1 mm厚)。为进一步提高信噪比,在同一位置重复接收多次后取平均。激发出的超声信号最后由数字示波器Tektronic DPO 4054B接收并实时显示。

图3 全光学型激光超声检测系统示意图Fig.3 Schematic diagram of the all-optical laser ultrasonic testing system
待检铝板尺寸为1 000 mm×1 000 mm×0.89 mm,在板上加工通槽模拟铝板处于有缺陷状态,将激励光斑作为原点,缺陷右端中心坐标为(150,495)。从接收侧看,待检铝板示意图如图4所示。本文分别在有缺陷和无缺陷两块铝板中开展试验研究。无缺陷铝板P1;以及有缺陷铝板P2,缺陷尺寸为20 mm×2 mm。信号激励接收方式按照图4所示,激励光斑位置保持不变,接收光斑起始位置与激励光斑相距10 mm,以步长0.2 mm沿x正方向过缺陷直线扫描接收,共采集1 301组数据。设置示波器采样率为50 MHz。

图4 待检铝板示意图(mm)Fig.4 Schematic diagram of the test aluminium plate(mm)
3 试验结果分析
3.1 激光Lamb波时间-空间波场分析
铝板P1和P2上接收得到的激光Lamb波时间-空间波场如图5所示。从图5中可以看出,随着激励和接收距离的增加,在时间上,波场信号的振动次数逐渐增加。这是因为激光Lamb波是宽频信号,当激励和接收距离较近时信号传播距离不够,各频率成分处于相互叠加状态,此时表现为各频率成分振动的合成;随着激励和接收距离的增加,各频率成分在传播过程中逐渐分离,表现出各自的传播特性。还可以看出,对于某一位置处接收到的Lamb波信号,在时间上的接收顺序为先高频后低频,而且低频成分能量较高;对于某一时刻空间上存在的Lamb波信号,表现为高频成分传播的距离更远。这是由于点光源激励出的激光Lamb波信号以低频为主,同时由于接收光束和铝板保持垂直,使得接收光束对Lamb波离面位移比较敏感,因此接收信号中主要为低频的A0模态。所以接收到的波场信号表现出,高频成分能量较低、波速较快,低频成分能量较高、波速较慢的特点,这和低频段内理论A0模态群速度随频率变化的规律一致。
对比图5(a)和图5(b)可以看出,入射的激光Lamb波信号在缺陷处发生了反射和绕射。借助时间-空间波场,直观地显示了激光Lamb波的传播特性。为进一步揭示激光Lamb波的传播特性,下面对激光Lamb波信号进行频率-波数分析。

图5 激光Lamb波时间-空间波场Fig.5 Time-space wavefield of laser-induced Lamb waves
3.2 激光Lamb波频率-波数分析
对激光Lamb波时间-空间波场做二维傅里叶变换得到频率-波数谱,将幅值取对数以便清楚地显示信号中包含的模态成分,如图6所示。图中虚线是0.89 mm厚铝板中Lamb波的理论频率-波数曲线。
从图6中可以看出,试验得到的激光激励Lamb波模态的频率-波数谱和理论频散曲线相吻合,其中不仅包含低阶模态A0,S0,还包含高阶模态A1,S1,低阶模态的能量大于高阶模态的能量,并且低频处A0模态的能量最强,和“3.1”节分析结论一致。同时从图6中还可以看到明显的能量泄漏成分。注意到,在图6(b)中存在负波数成分。负波数表示Lamb波传播方向和扫描方向相反,是缺陷处Lamb波反射信号在频率-波数域内的表现形式。为了得到某一中心频率下波数沿扫描路径的变化情况,下面进行空间-频率-波数分析。

图6 激光Lamb波时间-空间波场的频率-波数谱Fig.6 Frequency-wavenumber spectrum of time-space wavefield of laser-induced Lamb waves
3.3 激光Lamb波空间-频率-波数分析
本文以中心频率160 kHz为例,分析波数沿扫描路径的变化情况。选择宽度50 mm的二维汉宁窗,移动步长0.2 mm,对图5中的时间-空间波场信号进行短空间二维傅里叶变换,可得到中心频率160 kHz下的幅值-空间-波数谱,如图7所示。
图7直观地显示了沿扫描路径A0模态波数的变化情况。如图7(a)所示,对于无缺陷铝板,只存在入射波对应的波数谱。而对于缺陷铝板,除了入射波对应的波数谱,由缺陷引起的反射波和绕射波对应的波数谱都可以被直观的看到,如图7(b)所示。从图7中还可以看出,入射波、反射波以及绕射波对应的波数谱都集中在0.88 rad/mm位置处,和理论值较为一致(0.89 mm厚铝板中频率160 kHz的A0模态理论波数为0.89 rad/mm)。反射波是起始于缺陷相对于入射波反向传播的信号,如图7(b)所示,反射波对应的波数谱起始于理论缺陷位置(虚线为缺陷理论位置,D=150 mm)。因此,在幅值-空间-波数谱中,可根据反射波对应的波数谱的起始坐标确定缺陷的位置。注意到,图7中存在着一定的干扰成分,会影响Lamb波传播特性的分析以及缺陷识别。该干扰成分是由逐次二维傅里叶变换中产生的能量泄漏造成的。为了减小干扰的影响,需在进行空间-频率-波数分析之前对原始激光Lamb波信号进行预处理。
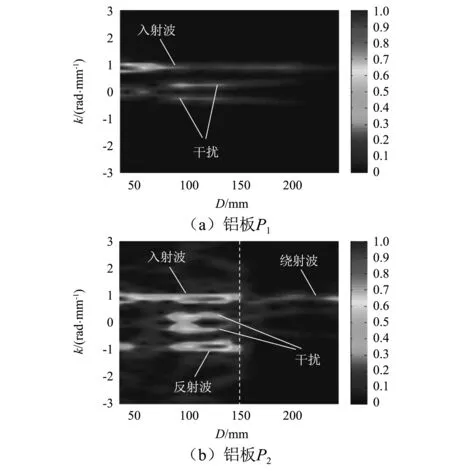
图7 中心频率160 kHz下的幅值-空间-波数谱Fig.7 Amplitude-space-wavenumber spectrum at the center frequency of 160 kHz
3.4 空间-频率-波数分析结果优化
低频处泄漏出来的能量和有用模态成分的能量相当,因此在幅值-空间-波数谱中可以看到明显的干扰成分。针对干扰存在的原因,本文采取从原始激光Lamb波信号中提取特定中心频率下窄带信号的方法,使信号能量集中在中心频率附近以减小干扰。利用连续小波变换可以从宽频Lamb波信号中提取出一个窄带的Lamb波信号[42]。由于各组激光Lamb波时域信号的特征差异较大,使用同一个母小波对整个波场信号进行提取效果不佳,给信号提取带来了不便。因此,对原始波场信号先进行带通滤波,在此基础上再利用连续小波变换获取单频信号。
根据小波系数的香农熵最小理论[43],选取gaus9为母小波,利用连续小波变换提取中心频率160 kHz的Lamb波信号。铝板P1上,接收光斑在距离激励光斑90 mm处接收到的Lamb波时域信号及其频谱如图8所示。如图8(a)所示为原始激光Lamb波时域信号,其中包含了一些高频噪声。图8(b)所示为原始激光Lamb波信号频谱,进一步可以看出,激光Lamb波信号频带宽且以低频为主。对原始激光Lamb波信号进行小波降噪后,利用带通滤波及连续小波变换提取中心频率160 kHz的Lamb波信号,结果如图8(c)所示,从中可以明显地看出直达波信号。图8(d)所示为利用带通滤波及连续小波变换提取中心频率160 kHz的Lamb波信号频谱,从中可以看出信号的频带已很好的集中在160 kHz附近。

图8 铝板P1中距离激励光斑90 mm处的激光Lamb波时域信号及频谱Fig.8 Time domain signal and spectrum of laser-induced Lamb waves at x=90 mm in aluminium plate numbered P1
铝板P2上,接收光斑在距离激励光斑90 mm处接收到的Lamb波时域信号及其频谱如图9所示。其中,图9(a)为原始激光Lamb波时域信号,该信号中包含许多高频噪声,从图中无法直观地看出直达波信号和缺陷回波信号,但根据0.06 ms以后信号幅值多次不规律振荡现象,可推断出该时刻后信号中同时包含了除直达波以外的其它成分。图9(b)为原始激光Lamb信号频谱。利用带通滤波及连续小波变换提取中心频率为160 kHz的Lamb波信号如图9(c)所示,从中可以直观地看出直达波和缺陷回波。图9(d)为利用带通滤波及连续小波变换提取的中心频率160 kHz的Lamb波信号频谱,可以看出信号的频带已很好的集中在160 kHz附近。
将图5中对应的1 301组激光Lamb波信号全部采用带通滤波结合连续小波变换的方法进行提取得到中心频率160 kHz的波场信号,如图10所示。相较于原始激光Lamb波波场信号,图10中更清楚地展现出Lamb波信号在缺陷附近的入射、反射和绕射现象。

图9 铝板P2中距离激励光斑90 mm处的激光Lamb波时域信号及频谱Fig.9 Time domain signal and spectrum of laser-induced Lamb waves at x=90 mm in aluminium plate numbered P2
对图10中的时间-空间波场信号进行二维傅里叶变换,结果如图11所示。提取后Lamb波信号的频率-波数谱和理论A0模态频散曲线相吻合,表明提取过程没有造成信号本身特性的改变,且能量已很好地集中在中心频率160 kHz附近。从图11(b)可以看出,负频率-波数谱的能量要低于正频率-波数谱的能量,与信号在整个传播过程中入射波和绕射波的总能量大于反射波能量的规律一致。

图10 中心频率160 kHz下 的时间-空间波场信号Fig.10 Time-space wavefield at the center frequency of 160 kHz
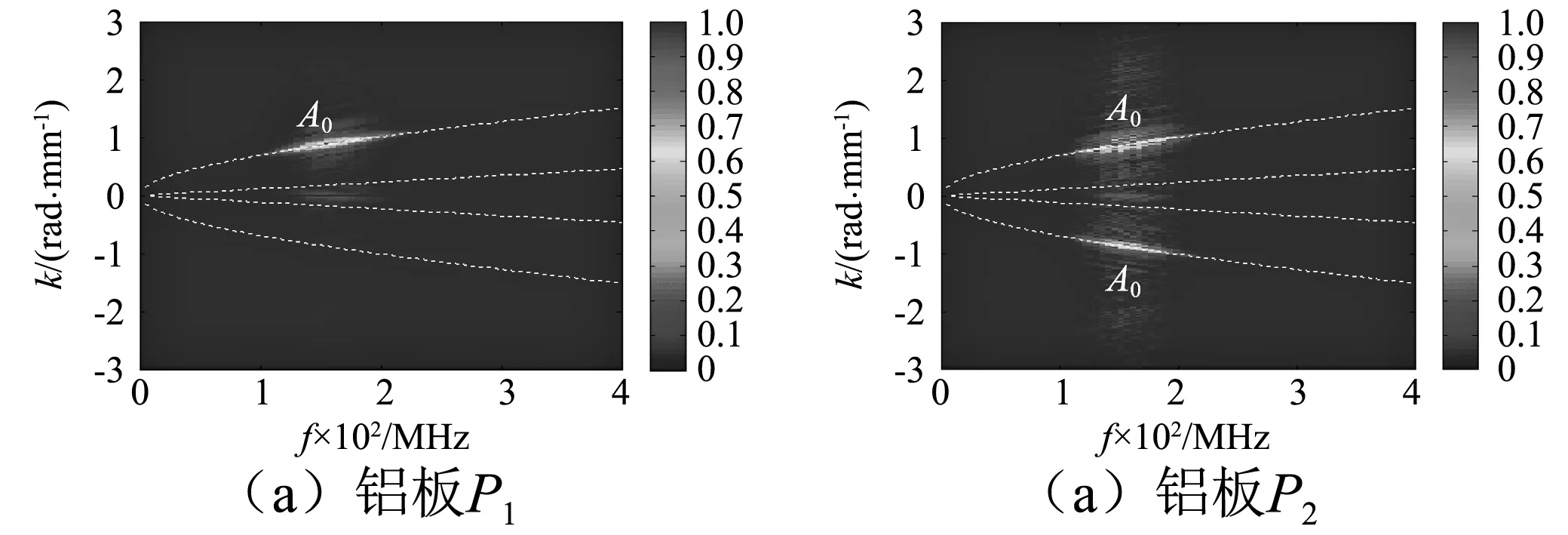
图11 中心频率160 kHz下的时间-空间波场信号 的二维傅里叶变换结果Fig.11 Two-dimensional Fourier transform results of time-space wavefield at the center frequency of 160 kHz
对提取后的波场信号进行短空间二维傅里叶变换,其它参数保持不变,结果如图12所示。从图中可以看到,经过带通滤波结合连续小波方法提取后幅值-空间-波数谱中的干扰得到了很好的消除。同时可以看出幅值-空间-波数谱具有较好的信噪比,

图12 中心频率160 kHz下的幅值-空间-波数谱Fig.12 Amplitude-space-wavenumber spectrum at 160 kHz center frequency
波数谱都集中在0.88 rad/mm位置处,和理论值较为一致。根据反射波对应的波数谱的起始坐标可有效确定缺陷的位置(虚线为缺陷理论位置,D=150 mm)。
4 结 论
相较于压电传感器激励的Tone burst信号,点光源激励、激光接收得到的Lamb波信号呈现宽频带并以低频为主的特点。激光Lamb波波场信号经二维傅里叶变换后在低频处产生的能量泄露会成为在频率较高处得到的幅值-空间-波数谱中的干扰,造成了伪波数成分的出现。对于壁厚减薄缺陷产生的新波数成分理论上在幅值-空间-波数谱中可以被直观的看到,利用波数和板厚之间的关系便可实现缺陷深度的定量评估,而伪波数成分的存在会使造成对板结构健康状况的误判断。因此,减弱低频成分能量泄露引起的干是十分必要的。在原有波数分析方法的基础上,通过带通滤波结合连续小波变换的方法提取单频信号有效的消除了泄露干扰。因此,本文的研究结果提供了一种针对波数分析算法的非接触缺陷定量检测的方法。

