高速圆柱滚子轴承保持架振动特性研究

张文虎， 胡余生， 邓四二， 徐 嘉， 胡永乐

(1. 河南科技大学 机电工程学院，河南 洛阳 471003；2. 空调设备及系统运行节能国家重点实验室，广东 珠海 519000)

圆柱滚子轴承由于较小的摩擦因数、优良的高速性能等优点，被广泛应用于航空发动机主轴、齿轮箱、机器人变速装置等机械传动系统中。对于高速运转的圆柱滚子轴承，滚子与保持架之间的频繁碰撞与摩擦将引起保持架的振动。研究表明：在高转速下，由于滚子对保持架的频繁碰撞与摩擦引起的保持架振动往往是引起保持架失效的主要原因之一[1-2]。因此，对于高速圆柱滚子轴承保持架振动特性的研究就显得非常重要。

国内外学者对滚动轴承保持架进行了广泛研究：Gupta[3-4]采用古典微分方程的方法建立了圆柱滚子轴承的动力学分析模型，研究了稳定工况下保持架的打滑和运行稳定性；立石佳男等[5]用三个涡流式传感器检测角接触球轴承保持架X，Y，Z方向的振动位移，测定在各种不同工作条件(转速、载荷、润滑及间隙)下的保持架涡动；Ghaisas等[6]基于简化的润滑剂拖动模型，研究了保持架兜孔间隙、引导间隙、滚子直径及内圈倾斜角对保持架涡动轨迹和保持架速度偏差比的影响，并使用保持架速度偏差评定保持架的稳定性； Selvaraj等[7]用试验方法分析了诸如转速、径向载荷、润滑油黏度、滚子个数和轴承温度等因素对圆柱滚子轴承保持架打滑的影响。研究结果表明：对于高速轴承，轴承元件动态的不稳定性是造成轴承失效的主要原因。Stevents[8]通过试验研究了角接触球轴承保持架的不稳定性。结果表明：保持架的不稳定表现为径向的高频振动。Tada[9]分别通过对理论与试验相结合的分析方法对角接触球轴承保持架的振动与噪声进行了分析。研究表明：通过调整预载荷、降低润滑油黏度及轴承旋转加速度、减小保持架不平衡量可以有效的降低保持架的振动与噪声。Zhang等[10]建立了高速圆柱滚子轴承动力学模型，分析了四种航空润滑油对保持架质心轨迹的影响，并使用了庞加莱图分析保持架的稳定性；杜辉等[11-14]基于滚动轴承的动力学理论，将保持架视为刚性体，研究了轴承工况参数与结构参数对保持架动态特性以及滚子的打滑和受载个数的影响。周延泽等[15]基于修正的Craig-Bampton子结构模态综合法，分析了保持架环平面内的弯曲振动、面外扭转振动等，并给出高阶共振和冲击作用是引起保持架疲劳断裂的主要原因。杨海生等[16]以滚动轴承的动力学理论为基础，将保持架进行柔性化处理，研究了高速圆柱滚子柔性保持架的动态特性，并对保持架的模态和应力分布情况进行了分析。刘秀海[17]在Gupta等的动力学模型基础上，考虑了油膜阻尼与黏滞阻尼的影响，建立了高速油润滑圆柱滚子轴承的动力学分析模型，较为全面的研究了轴承载荷、转速、保持架的间隙比以及滚动体数量等因素对高速轴承的保持架动态特性影响。邓四二等[18]建立了圆柱滚子轴承动力学分析模型，研究了保持架引导方式、内外套圈旋转方式以及保持架间隙比对保持架质心轨迹和打滑率的影响。姚廷强等[19]分析了工况条件对圆柱滚子轴承的内圈中心振动、滚子倾斜扭转振动及保持架轴向振动的影响。赖拥军等[20]在弹性流体动力润滑的基础上提出一个高速球轴承保持架振动响应模型，并建立了保持架的动力学方程，对某型号航空发动机的主轴承保持架进行研究，研究表明：高阶共振与过渡过程的冲击作用是导致保持架疲劳断裂的重要原因。覃庆权等[21]针对10 MW高温气冷堆氦气汽轮机发电系统(HTR-10 GT)中的辅助球轴承的工作特点，采用有限元方法研究分析了保持架的离心应力与自由振动特性，并讨论了不同结构参数对保持架振动特性的影响。

综上所述，国内外对于保持架特性的研究主要集中在轴承的工况参数、结构参数以及润滑剂对保持架的动态性能的影响方面。而对于保持架振动特性的研究，主要采用有限元的方法，且集中在球轴承的保持架方面，而有关保持架振动的试验研究方面也较少，对于高速圆柱滚子轴承保持架振动特性方面的研究相对匮乏。鉴于此，本文在滚动轴承动力学理论的基础上，建立高速圆柱滚子轴承非线性动力学微分方程组，研究高速圆柱滚子轴承结构参数与工况参数等因素对保持架振动特性的影响。本文的研究结果可为高速圆柱滚子轴承的结构设计和使用提供一定的理论依据。

1 高速圆柱滚子轴承动力学模型

本文研究的高速圆柱滚子轴承采用4109航空润滑油进行润滑，外圈固定，内圈旋转，保持架由外圈引导，并假设轴承各零件的质心和形心重合，且不存在加工误差。

1.1 圆柱滚子轴承的坐标系

根据圆柱滚子轴承的结构特点，建立以下五种坐标系(见图1)：

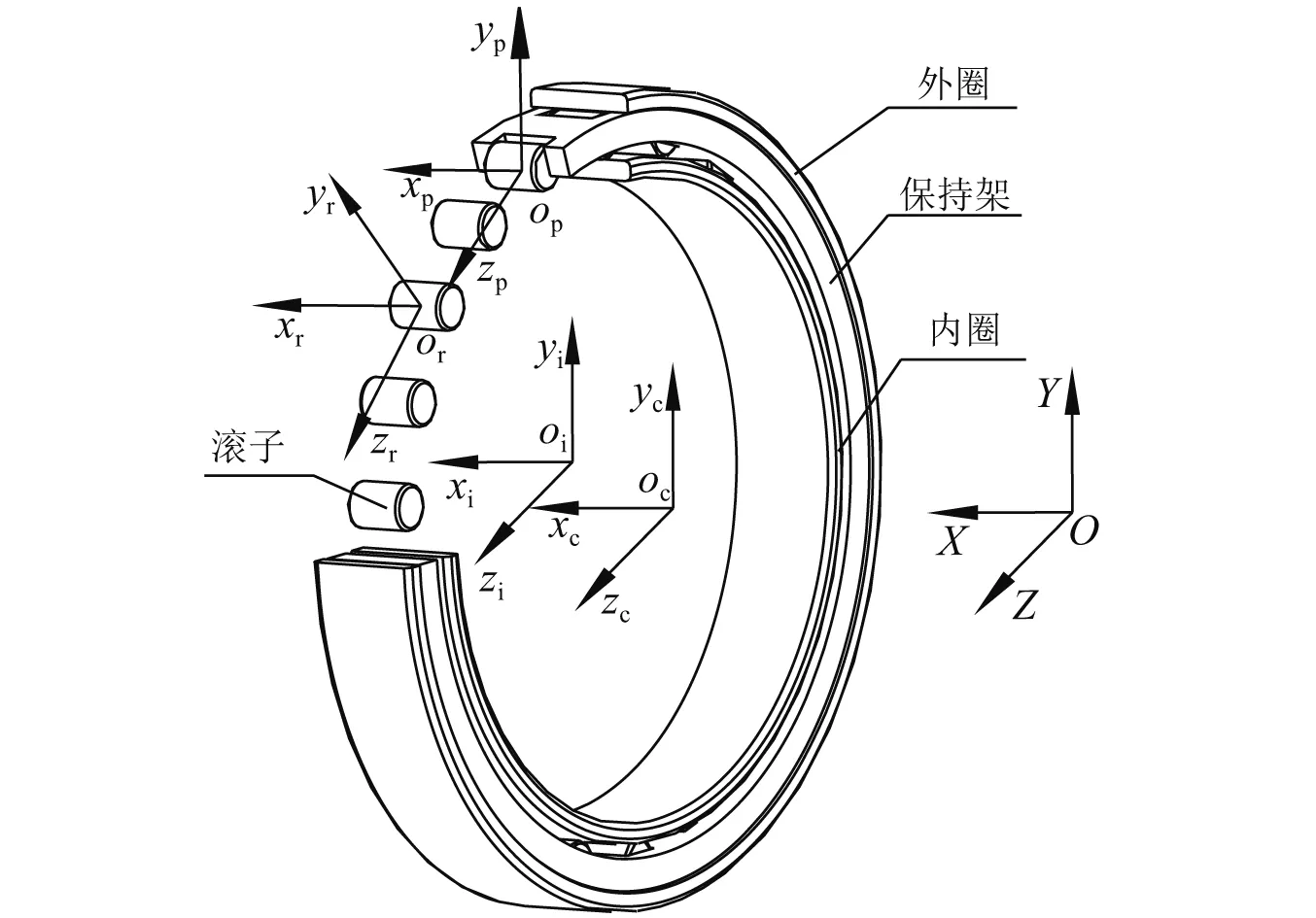
图1 圆柱滚子轴承坐标系Fig.1 Coordinate system of cylindrical roller bearing

(1) 轴承惯性坐标系{O;X,Y,Z}，X轴与轴承转轴重合，YZ面与通过轴承中心的径向平面平行。此坐标系在空间中固定不变，其他坐标系均参照此坐标系来确定；

(2) 滚子质心坐标系{or;xr,yr,zr}，此坐标系的原点or与滚子的几何中心重合，yr轴沿轴承径向方向，zr轴沿轴承周向方向。此坐标系随着滚子中心一起移动，但不随滚子自转，每个滚子都有属于自己的滚子局部坐标系；

(3) 保持架质心坐标系{oc;xc,yc,zc}，此坐标系由惯性坐标系{O;X,Y,Z}平移得到，坐标原点oc与保持架几何中心重合，坐标系随保持架一起移动和旋转；

(4) 内圈质心坐标系{oi;xi,yi,zi}，此坐标系由惯性坐标系{O;X,Y,Z}平移得到，坐标原点oi与内圈几何中心重合，坐标系随内圈一起移动和旋转；

(5) 保持架兜孔中心坐标系{op;xp,yp,zp}，此坐标系开始时与滚子质心坐标系重合，以后随保持架一起移动和旋转，此坐标系的原点op与保持架兜孔几何中心重合，每个兜孔都有属于自己的局部坐标系。

工作前后的圆柱滚子轴承示意图如图2所示。

图2 圆柱滚子轴承示意图Fig.2 Schematic diagram of cylindrical roller bearing

图2中，Oi，O′i为轴承工作前、后的内圈中心位置；Fr为施加在轴承内圈上的径向载荷；ur为轴承的径向游隙；ωi为轴承内圈角速度；φj为第j个滚子的方位角。

1.2 滚子非线性动力学微分方程组

高速圆柱滚子轴承在工作过程中，滚子受到内、外滚道对其的法向作用力、油膜拖动力、保持架的碰撞力和滚子自身的离心力以及它们所产生的附加力矩的共同作用，滚子的受力如图3所示，图3中所有作用力及力矩的表达式参考文献[22]。

图3 滚子受力示意图Fig.3 Schematic diagram of roller forces

滚子的非线性动力学微分方程组可表示为

(1)

1.3 保持架非线性动力学微分方程组

圆柱滚子轴承在启动过程中，其保持架受到滚子的碰撞力、(内)外圈的引导力以及油/空气混合物对保持架的端面和表面的阻力的共同作用，保持架的受力示意图如图4所示。

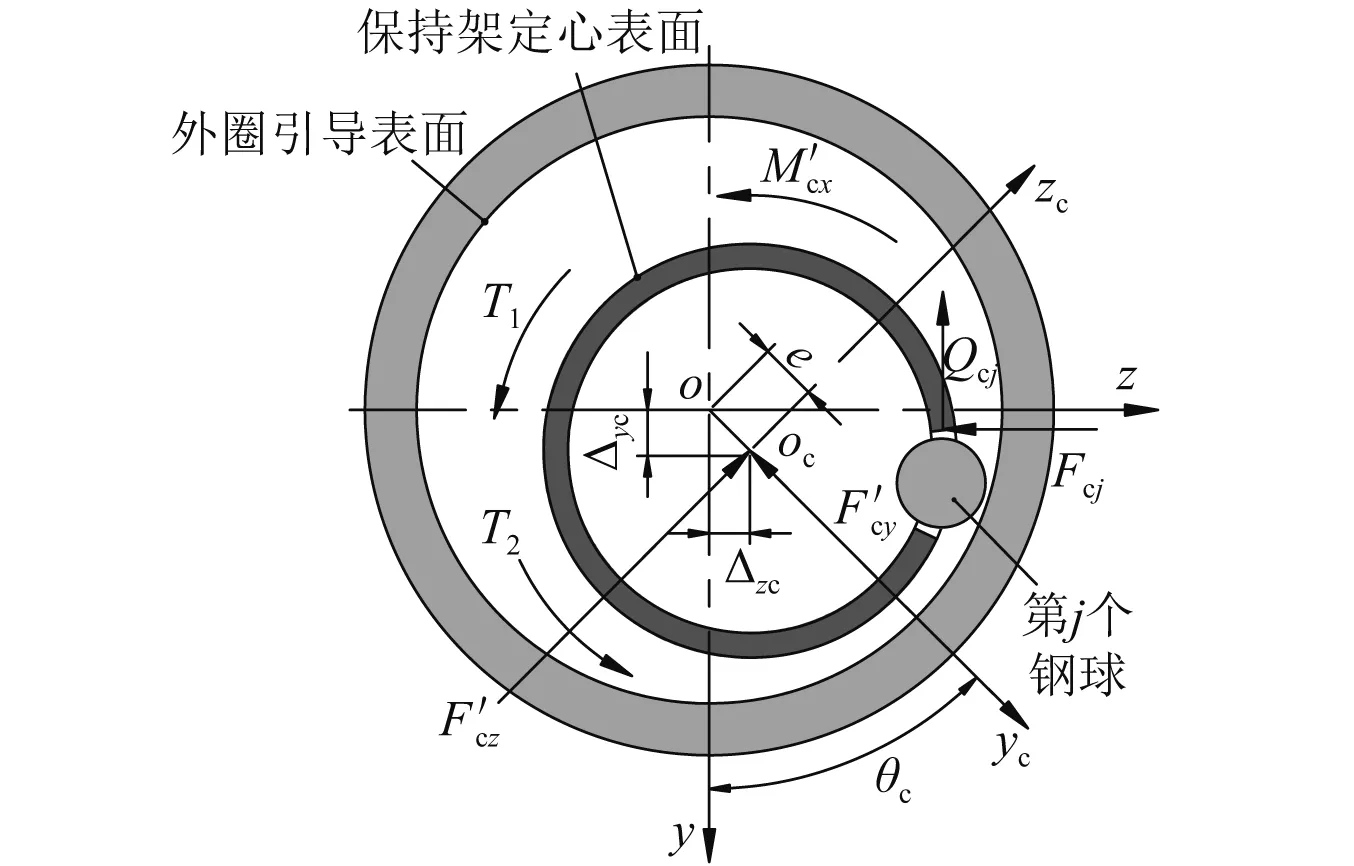
图4 保持架受力示意图Fig.4 Schematic diagram of cage forces

保持架的非线性动力学微分方程组如式(2)所示

(2)

1.4 内圈非线性动力学微分方程组

内圈受到滚子和径向载荷的共同作用。内圈的非线性动力学微分方程组如式(3)所示

(3)

2 高速圆柱滚子轴承保持架振动特性分析

以某型号高速圆柱滚子轴承为研究对象，采用GSTIFF变步长积分算法求解轴承的非线性动力学微分方程组(见式(1)～式(3))，研究轴承结构参数(径向游隙、保持架引导间隙、保持架兜孔周向间隙)与工况参数(径向载荷、轴承转速)对高速圆柱滚子轴承保持架振动特性的影响。轴承的主参数如表1所示。

表1 轴承主参数Tab.1 Main parameters of bearing

本文通过研究保持架Y向(即：径向载荷Fr方向)振动加速度的时域、频谱以及振动加速级，进而对保持架的振动进行评价。其中，振动频谱通过对振动加速度进行快速傅里叶变换(Fast Fourier Tranform,FFT)得到，保持架的振动加速度级定义为[23]

(4)

式中：Lrms单位为dB;arms为振动信号的均方根值,m/s2;a0为参考加速度级，a0=9.81×10-3m/s2。

2.1 径向载荷对保持架振动特性的影响

当轴承径向间隙为0.06 mm，保持架引导间隙为0.6 mm，保持架兜孔周向间隙为0.2 mm，保持架兜孔轴向间隙为0.2 mm，轴承转速为10 000 r/min，轴承径向载荷范围为1 000～5 000 N，研究径向载荷对保持架振动特性的影响。

图5为不同径向载荷下保持架的振动加速度。图6为不同径向载荷下保持架的振动频谱图。图7为径向载荷对保持架振动加速度级的影响规律。

图5 不同径向载荷下保持架振动加速度Fig.5 Vibration acceleration of cage under various radial loads

图6 不同径向载荷下保持架的振动频谱图Fig.6 Vibration spectrum of cage under various radial loads

图7 径向载荷对保持架振动加速度级的影响Fig.7 Effect of radial load on cage’s vibration acceleration level

由图5可知：随着径向载荷的增加，保持架振动加速度的最大值呈减小的趋势。由图6可知：随着径向载荷的增加，fc，2fc，3fc(fc为保持架涡动频率)对应的幅值都呈减小的趋势，但其4fc处对应的幅值呈现先减小后增加再减小的趋势；随着径向载荷的增加，保持架的5fc及更高倍频处的振幅显著降低，甚至消失。由图7可知：随着径向载荷的增加，保持架的振动加速度级呈现逐渐减小的趋势。

通过对图5～图7的分析可知：随着径向载荷的增加，保持架的振动随之减弱。导致上述现象的主要原因是：随着径向载荷的增加，使得轴承承载区的滚子个数增加，推动保持架转动的滚子个数增加，滚子与兜孔横梁间的摩擦力增大，导致保持架在径向平面内受到限制，保持架振动减小。

2.2 轴承转速对保持架振动特性的影响

当轴承径向游隙为0.06 mm，保持架引导间隙为0.6 mm，保持架兜孔周向间隙为0.2 mm，保持架兜孔轴向间隙为0.2 mm，径向载荷为3 000 N，轴承转速范围为8 000～16 000 r/min，研究轴承转速对保持架振动特性的影响。

图8为不同转速下保持架的振动加速度。图9为不同转速下保持架的振动频谱图。图10为轴承转速对保持架振动加速度级的影响规律。

图8 不同转速下保持架的振动加速度Fig.8 Vibration acceleration of cage under various rotational speeds

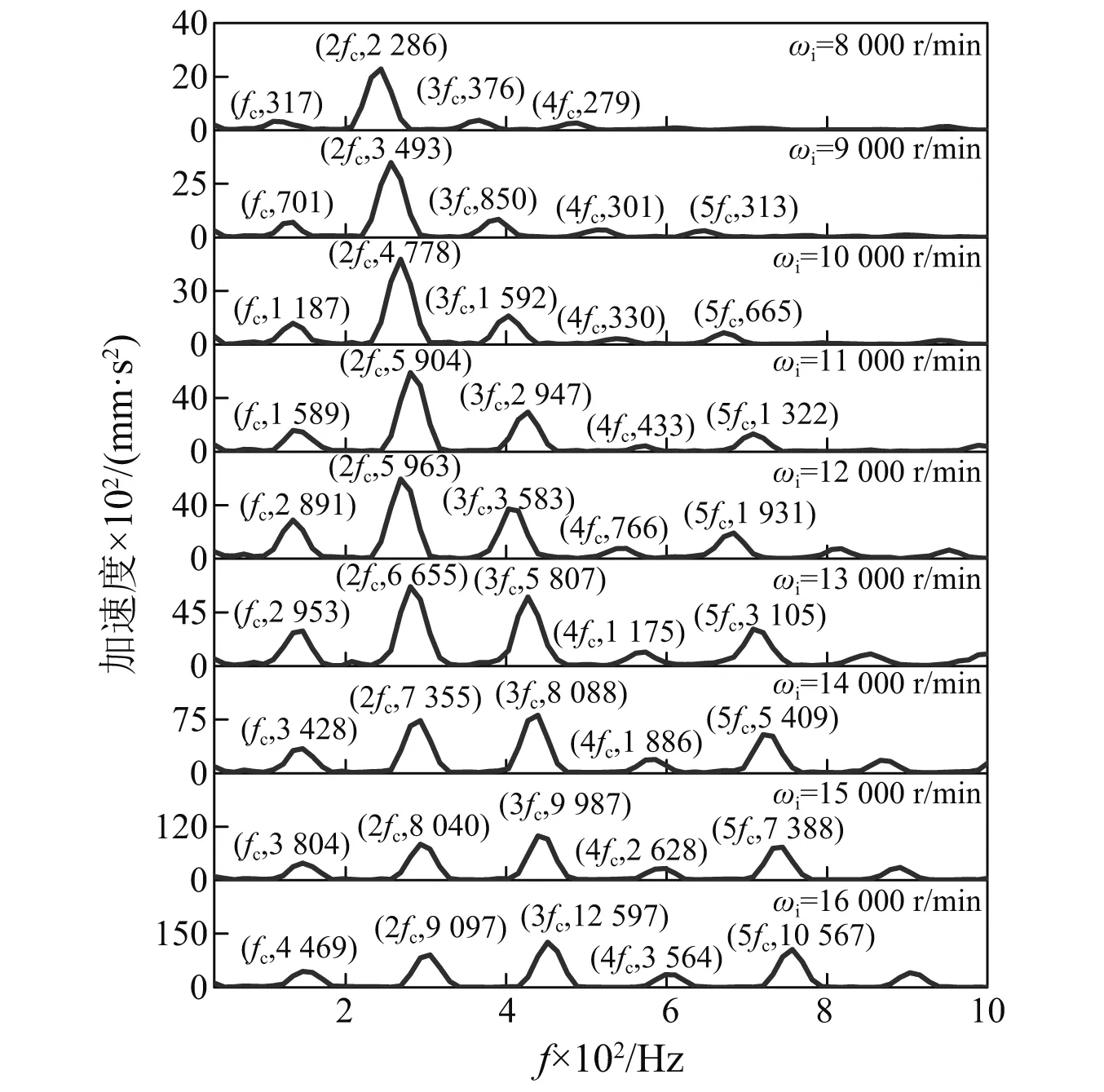
图9 不同转速下保持架的振动频谱图Fig.9 Vibration spectrum of cage under various rotational speeds

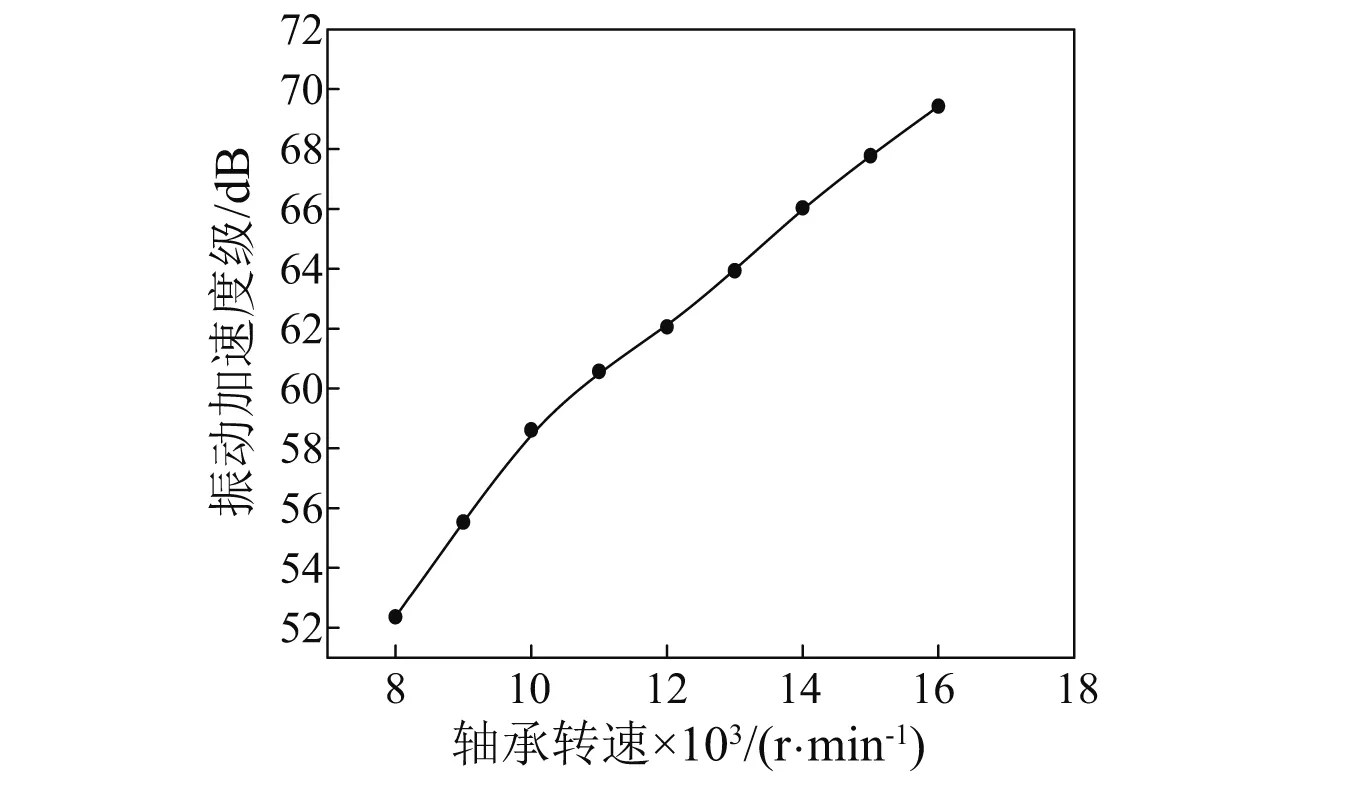
图10 轴承转速对保持架振动加速度级的影响Fig.10 Effect of rotation speed on cage’s vibration acceleration level

由图8可知：随着轴承转速的增加，保持架的振动加速度呈现增加的趋势。由图9可知：随着转速的增加，fc与其各倍频处对应的幅值都呈增大的趋势；同时，随着轴承转速的增加，保持架的5fc及更高倍频处的振幅显著增加，保持架可能发生高频振动。由图10可知：随着轴承转速的增加，保持架的振动加速度级呈现增大的趋势。

通过对图8～图10的分析可知：随着轴承转速的增加，保持架的振动随之增大。导致上述现象的主要原因是：随着轴承转速的增加，滚子离心力增大，使得滚子外抛，内滚道对滚子的拖动力减小，导致滚子与保持架兜孔横梁之间的摩擦力减小，对保持架径向振动的限制降低，振动范围增加，同时滚子推动保持架的作用力变得不均匀，滚子与保持架的之间的转速差变大，滚子对保持架的冲击频率增加，从而使得保持架的振动增加。

2.3 轴承径向游隙对保持架振动特性的影响

当保持架引导间隙为0.6 mm，保持架兜孔周向间隙为0.2 mm，保持架兜孔轴向间隙为0.2 mm，径向载荷为3 000 N，轴承转速为10 000 r/min，轴承径向游隙变化范围为0～0.2 mm时，研究径向游隙对保持架振动特性的影响。

图11为不同径向游隙下保持架振动加速度。图12为不同径向游隙下保持架振动频谱图。图13为径向游隙对保持架振动加速度级的影响规律。

由图11可知：随着轴承径向游隙的增加，保持架的振动加速度随之增大。由图12可知：当轴承径向游隙小于0.12 mm，随着轴承径向游隙的增加，fc，2fc，3fc与5fc处对应的幅值都呈增大的趋势；当轴承径向游隙大于0.12 mm时，fc，2fc与3fc处对应的幅值随着轴承径向间隙的增加而增加，但其增加幅值较小；轴承径向间隙对保持架4fc处幅值的影响比较复杂。由图13可知：当轴承径向游隙在0～0.05 mm内时，随着轴承径向游隙的增加，保持架振动加速度级迅速增加，幅度增加较大；当轴承径向游隙在0.05～0.20 mm时，随着轴承径向游隙的增加，保持架振动加速度级增加，但增加幅度较小。

图11 不同径向游隙下保持架的振动加速度Fig.11 Vibration acceleration of cage under various radial clearances

图12 不同径向游隙下保持架的振动频谱图Fig.12 Vibration spectrum of cage under various radial clearances

通过对图11～图13的分析可知：随着轴承径向游隙的增加，保持架的振动随之增大，较小的径向游隙有利于降低保持架的振动。导致上述现象的主要原因是：随着径向游隙的增加，轴承的受载区域减小，承载当径向游隙为0.06 mm，保持架兜孔周向间隙为0.2 mm，保持架兜孔轴向间隙为0.2 mm，轴承径向载荷为3 000 N，轴承转速为10 000 r/min，保持架引导间隙uy变化范围为0.2～1.2 mm时，研究引导间隙对保持架振动特性的影响。

图13 径向游隙对保持架振动加速度级的影响Fig.13 Effect of radial clearance on cage’s vibration acceleration level

滚子个数减少，保持架转速变化范围较大，同时承载滚子受到作用力增大，使得滚子对保持架的冲击作用增加，导致保持架的振动加剧。

2.4 保持架引导间隙对保持架振动特性的影响

图14为不同保持架引导间隙下保持架的振动加速度。由图14可知：随着保持架引导间隙的增加，保持架的振动加速度呈现先降低后增加的趋势。说明过小或过大的保持架引导间隙均不利于降低保持架径向方向的振动。

图15为不同保持架引导间隙下保持架的振动频谱图。通过图15可知：当保持架引导间隙小于0.5 mm时，随着保持架引导间隙的增加，fc与其各倍频处对应的幅值呈现迅速减小的趋势；当保持架引导间隙大于0.5 mm时，fc，2fc，3fc，4fc及5fc处对应的幅值随着轴承引导间隙的增加而增加，说明存在一个最佳的保持架引导间隙使保持架在径向方向的振动最小。同时从图15中可以明显观察到：随着保持架引导间隙的增加，保持架的涡动频率fc的大小减小，产生这一现象的主要原因是：随着保持架的引导间隙增加，保持架涡动半径也随之增加，在转速不变的条件下，其涡动频率减小。

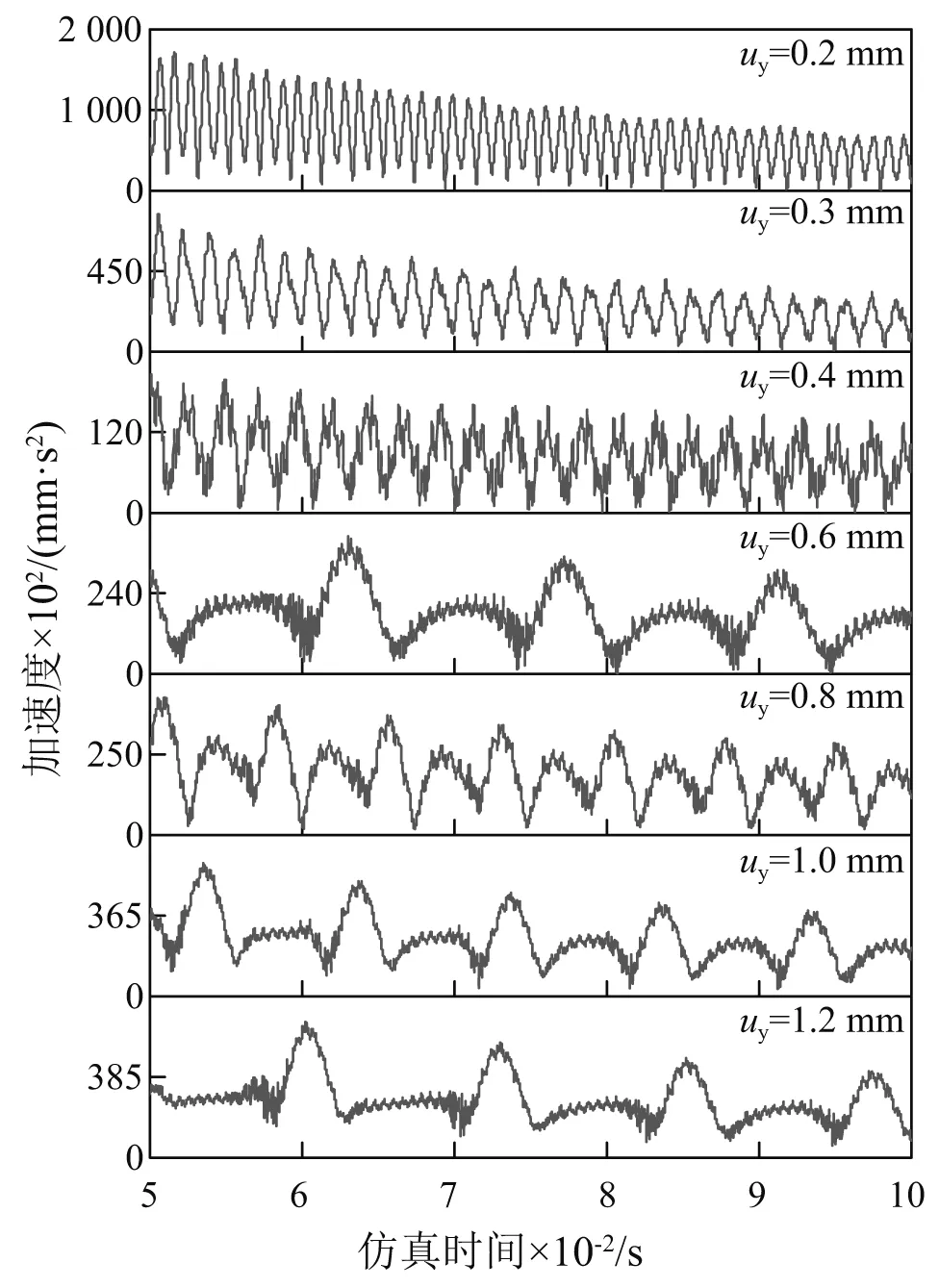
图14 不同引导间隙下保持架的振动加速度Fig.14 Vibration acceleration of cage under various guide-land clearances

图15 不同引导间隙下保持架的振动频谱图Fig.15 Vibration spectrum of cage under various guide-land clearances

图16为保持架引导间隙对保持架振动加速度级的影响规律。由图16可知：当保持架引导间隙小于0.5 mm时，随着保持架引导间隙的增加，保持架的振动加速度级随之减小，减小的幅度较大；当保持架的引导间隙大于0.5 mm时，随着保持架的引导间隙的增加，保持架的振动加速度级随之增加。说明过大或过小的保持架引导间隙均不利于降低保持架径向方向的振动。

从图14～图16可以得到：随着保持架兜孔周向间隙的增加，保持架的振动呈现减小后增大的趋势，存在一个最佳的保持架引导间隙范围使得保持架的振动较小。导致上述现象的主要原因是：当保持架引导间隙较小时，保持架将于引导套圈发生频繁的激烈碰撞，使保持架振动加大；当保持架引导间隙过大时，引导套圈对保持架的引导作用被弱化，滚子与保持架的频繁碰撞将成为保持架振动的主要原因。

图16 引导间隙对保持架振动加速度级的影响Fig.16 Effect of guide land clearance on cage’s vibration acceleration level

2.5 保持架兜孔周向间隙对保持架振动特性的影响

当轴承径向游隙为0.06 mm，保持架引导间隙为0.6 mm，保持架兜孔轴向间隙为0.2 mm，轴承径向载荷为3 000 N，轴承转速为10 000 r/min，保持架兜孔周向间隙ucr变化范围为0.05～0.6 mm时，研究保持架兜孔周向间隙对保持架振动特性的影响。

图17为不同保持架兜孔周向间隙下保持架的振动加速度。图18为不同保持架兜孔周向间隙下保持架的振动频谱图。

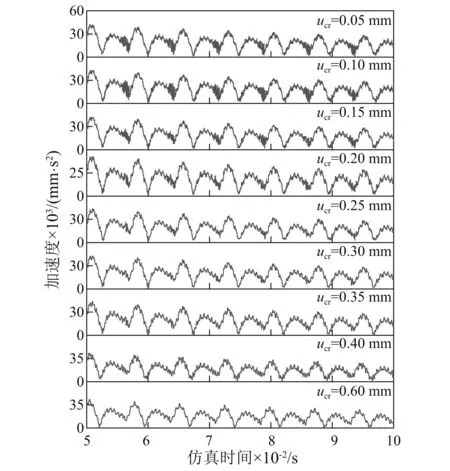
图17 不同兜孔周向间隙下保持架振动加速度Fig.17 Vibration acceleration of cage under various pocket circumference clearances

由图17可知：随着保持架兜孔周向间隙的增加，保持架的振动加速度呈现减小后增大的趋势。图18则可明显看出：随着保持架兜孔周向间隙的增加，保持架fc及其各倍频处对应的幅值呈先减小后增加的趋势。

图18 不同兜孔周向间隙下保持架的振动频谱图Fig.18 Vibration spectrum of cage under various pocket circumference clearances

图19为不同保持架兜孔周向间隙对圆柱滚子轴承的保持架振动加速度级的影响规律。通过图19可知：当保持架兜孔周向间隙小于0.2 mm时，随着兜孔周向间隙的增加保持架的振动加速度级呈现减小的趋势；当保持架兜孔周向间隙大于0.2 mm时，保持架振动加速度级随着兜孔周向间隙的增加呈现增大的趋势。

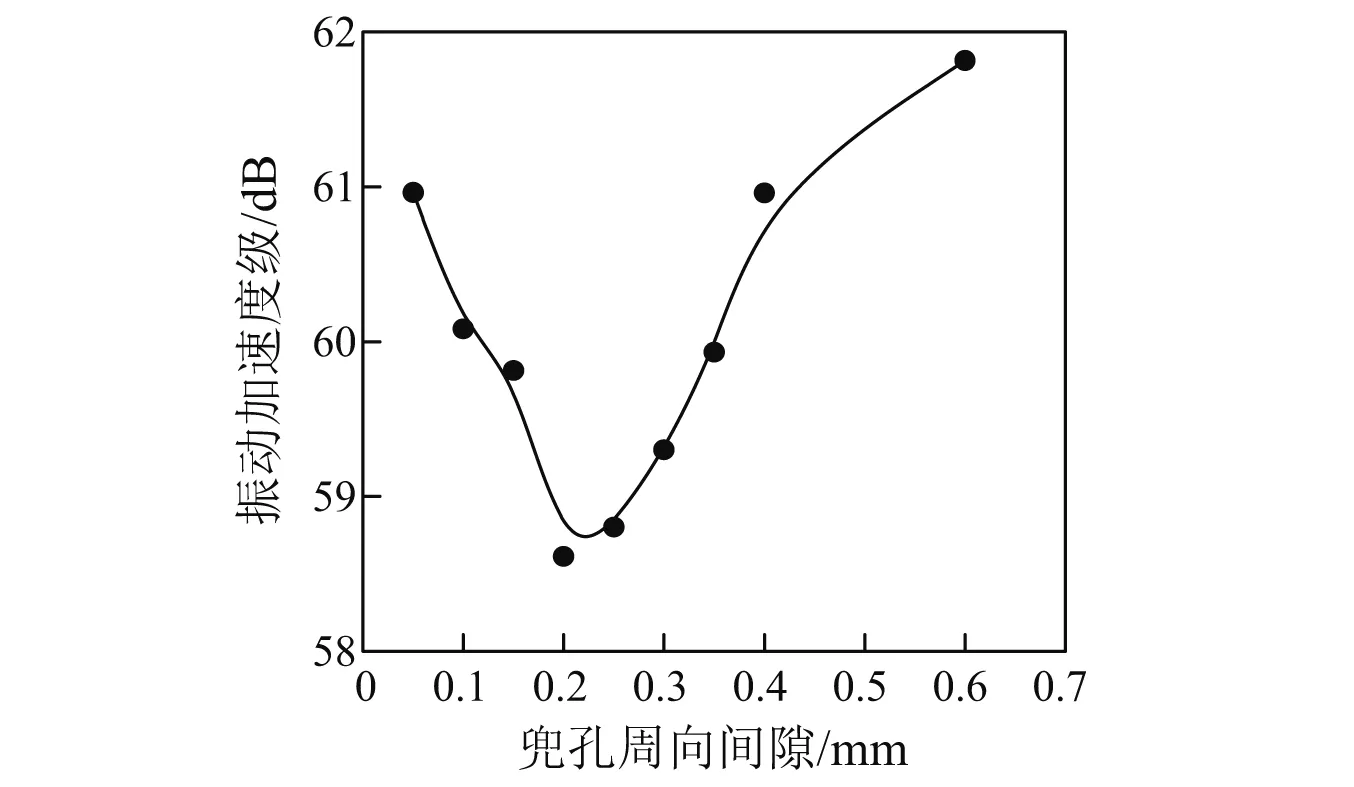
图19 兜孔周向间隙对保持架振动加速度级的影响Fig.19 Effect of pocket circumference clearance on cage’s vibration acceleration level

从图17～图19可以得到：随着保持架兜孔周向间隙的增加，保持架的振动呈现减小后增大的趋势，存在一个最佳的兜孔周向间隙范围使得保持架的振动较小。导致上述现象的主要原因是：当保持架兜孔间隙较小时，随着兜孔间隙的增加，滚子与保持架兜孔之间的冲击频率降低，使得保持架振动减小；当兜孔间隙过大时，随着兜孔周向间隙的增加，滚子对保持架的限制降低，使得保持架振动增加。

3 试验验证

本文采用航空发动机主轴轴承保持架动态性能试验机测量保持架的打滑率，以验证本文所建立模型和计算结果的正确性，试验机如图20所示。试验机中采用磁敏元件—霍尔元件对保持架的转速进行测量。磁块在保持架的安装位置如图21所示，在保持架的基准面上间隔180°对称镶嵌两个反向安装的磁块。通过测量得到保持架的转速换算得到保持架的打滑率，并与仿真结果进行对比。

图20 保持架性能试验机Fig.20 Testing machine for cage’s performance

图21 保持架磁块镶嵌示意图Fig.21 Schematic diagram of cage’s magnetic patch installation

当轴承转速为10 000 r/min，径向载荷范围为1 000～5 000 N时，保持架打滑率对比图如图22所示。当径向载荷为3 000 N，轴承转速范围为8 000～12 000 r/min时，保持架打滑率如图23所示。

图22 径向载荷对保持架打滑率的影响Fig.22 Effect of radial loads on cage’s slip ratio

图23 轴承转速对保持架打滑率的影响Fig.23 Effect of bearing speeds on cage’s slip ratio

由图22和图23可知：试验测的保持架打滑率与本文计算得到的保持架打滑率随径向载荷和轴承转速的变化规律基本一致，两者之间的具有一定的误差，但最大误差不超过15%，说明本文所建动力学模型与计算结果较为正确性。

4 结 论

(1) 轴承的工况条件对保持架的影响较大，适当的增大径向载荷有利于降低保持架在径向平面内的振动，而过高的轴承转速则会加剧保持架在径向平面内的振动。

(2) 随着轴承径向游隙的增加，保持架在径向平面内的振动先迅速增加后缓慢增加。因此，在保证轴承其它性能要求的前提下，可以适当减小轴承径向设计游隙或在安装过程中适量增加的径向预紧来降低保持架的振动。

(3) 过大或过小的保持架引导间隙和兜孔间隙均会加剧保持架的振动，存在一个最佳的保持架引导间隙和兜孔周向间隙设计范围能够有效的降低保持架振动。

致谢

感谢空调设备及系统运行节能国家重点实验室的支持。