基于柔性单元的一维列车碰撞模型及参数校正

秦睿贤， 周俊先， 陈秉智

(大连交通大学 机械工程学院， 辽宁 大连 116028)

耐撞性已成为轨道车辆的重点研究问题之一，列车在受到冲击后的结构响应得到了越来越多的关注, 现有轨道车辆均采用被动安全设计来最大程度上降低在突发事故中的人员伤亡与货物损失[1-2]。尤其是在2008年欧洲规范[3]发布以后，新车型均要进行耐撞性的评估。目前的列车级耐撞性评估方法主要有两类：数值模拟;实物实验。试验周期长,可重复性差,成本高等因素是实验可行性低的主要因素，新造列车进行完整的编组耐撞性实验在世界上尚未有先例,但是编组缩比实验已取得进展[4]。

基于显式动力分析方法进行列车级的碰撞分析时，求解机时长，数据规模较大，至少在目前的硬件条件下采用完整列车有限元模型进行能量设计方案选优是不经济的。单纯从数学模型角度来求解复杂结构的碰撞响应是非常复杂的，为了降低单次分析时间， 用于车辆碰撞分析的简化模型得到了大量研究，基于多体动力学方法，众多学者建立了不同的简化模型，在节省机时的同时可以准确预测列车碰撞响应。

简化模型[5-7]及参数校正[8-9]在汽车的碰撞研究中应用较多。小波分析,基于实车碰撞实验数据的集中参数模型参数校正方法,非线性回归模型和前馈神经网络等被用于研究车辆碰撞响应的预测和重现[10-13]。弹簧质量模型的适用性也得到了广泛研究，Pawlus等[14]研究了基于试验数据的车辆简化模型参数，从车辆动态响应和能量吸收方面确定了简化模型与实际模型的一致性；Klausen等[15]建立了非线性刚度阻尼特征的单弹簧模型用于车辆碰撞分析，采用萤火虫算法反求刚度阻尼参数，并对比了不同简化模型与实际碰撞实验数据的结果差异。

简化模型在铁路车辆中的应用也逐渐丰富，LU[16]较早地采用线性弹簧质量模型研究了不同编组下的各车辆连挂界面处的能量吸收情况。Fmilho等[17]、Milho等[18]提出一种验证过的多体模型用于列车耐撞性元件设计，并讨论了模型简化方法在碰撞元件设计中的适用性。李本怀等[19]提出了一种质量-弹簧能量分配方法, 用于设计前期快速匹配B型车设置压缩吨位和吸能区参数关系。除了传统的质量弹簧模型，新的单元也被广泛用于简化模型的构建。Moumni等[20]提出一种包含梁单元、塑性铰、非线性接触弹簧、刚体块的简化模型，成功用于车辆设计前期的碰撞过程的变参数分析。Dias等[21-22]基于塑性铰提出了一种刚柔多体动力学模型对多节编组列车进行了概念设计阶段的耐撞性指标优化，获取了最佳耐撞性指标下的设计方案。唐兆等[23]采用机器学习方法获得了碰撞过程中车辆的刚度与阻尼特性，获得了简化模型与实际模型较好的结果一致性。已有研究成果表明，在列车碰撞问题中采用简化模型是可行的，但是对车体的建模考虑较少，实际车体在冲击过程中的响应是不可忽略的。

本文在已有研究的基础上，提出了一种列车碰撞模型中车体的简化方法，并对车体等效单元进行了参数校正，建立了一种包含参数校正的非线性杆元、质量单元、非线性弹簧单元的列车一维碰撞模型，可用于列车初期能量优化配置参数研究。

1 车体纵向特性

碰撞过程的列车可以看作是一个多体能量耗散系统，冲击波从车头碰撞界面依次向尾车传播，应力波的反射会造成编组中的每辆车都将受到多次不同程度的压缩与拉伸，头车在车钩剪切失效后，车体前端成为被撞击面，压缩载荷方向更接近车体的纵向中心线，车体受载响应过程更接近于轴向压缩；而中间列车，以第二节为例，由于中间车钩不具备剪切功能，车体压缩载荷与纵向中心线偏离，压缩载荷对车体产生显著弯矩。根据受到载荷形式不同和外形结构差异，在列车编组中选择头车Tc与第二节中间车M为典型车辆，分析车体在受到冲击时的响应过程。

头车Tc和中间车M的有限元计算模型见图1，车辆一位端放置刚性墙块体，质量为20 000 kg，转向架与轨道之间建立主从接触关系，车辆二位端车钩安装位置处施加三向位移约束，刚性墙对车辆的冲击速度参考文献[3]中对固定编组列车对撞情景的速度设置为36 km/h。车钩采用非线性弹簧模拟，输入车钩力-行程曲线。在PAM-CRASH软件中对2辆车的冲击工况进行求解计算，输出在冲击过程中刚性墙块体的纵向速度、位移时程曲线，数据输出间隔设置为1 ms。

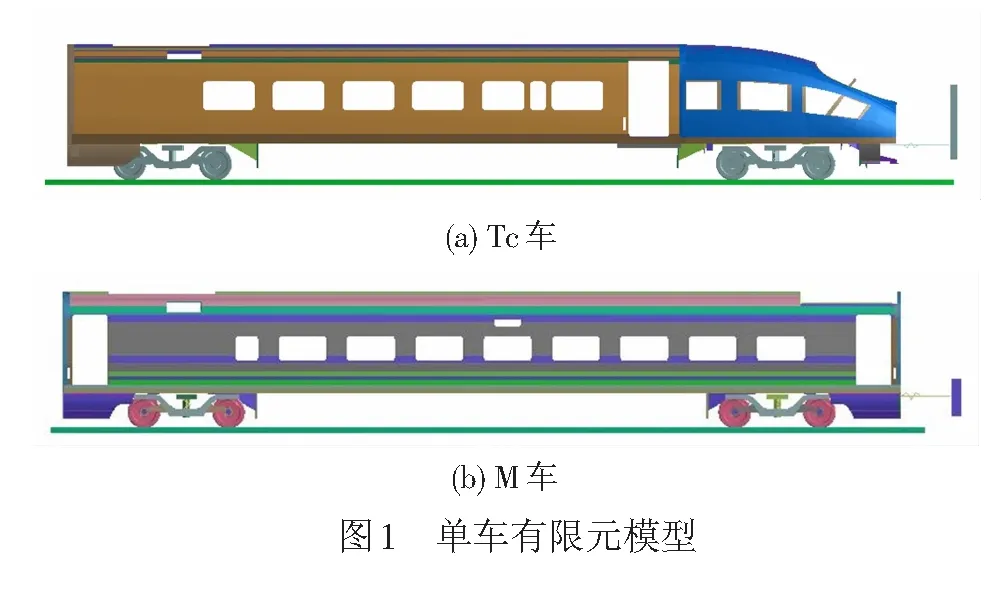
单车模型分析主要是为了获取冲击车体过程中刚性墙的速度、位移时程曲线，用于本文第4节中与一维模型进行数据匹配。车体受到的撞击力与车体纵向变形曲线见图2，车体的载荷-行程曲线将作为一维模型中车体的初始等效刚度。

2 单车简化模型

由于车体结构包含了较多的不规则几何特征，显然，获得车体在特定方向上的刚度与阻尼参数的理论解析解是很困难的，较为可行的办法是通过优化方法与有限元分析结合，获得较为接近的数值解。

为了获取非线性杆元模拟车体纵向响应特征时的等效参数，在图1所示的列车完整有限元模型上进行简化，去除转向架、轨道、车体等部分，只保留车钩弹簧单元、刚性墙，以非线性杆单元代替车体，建立单车碰撞的一维模型，见图3，其边界条件施加与本文第1节中实际车辆计算模型完全保持一致。

图3所示的非线性杆单元可以视为广义Kelvin模型，可以通过非线性函数来定义弹簧和阻尼的力学行为，杆元的纵向力为

( 1 )

δ=L-L0

( 2 )

( 3 )

通过两种不同模型下获得的刚性墙的纵向响应的一致性来反求简化模型中杆元的等效参数，主要是杆元纵向加载时的刚度与阻尼特征曲线，完成单节车辆在指定边界条件下的参数校正。

3 参数校正

单车的参数校正问题可采用优化方法进行求解，使得一维模型的响应输出结果与实际模型求解结果的拟合度达到匹配的参数就是要求解的优化问题的最优解。分别提取三维模型与一维模型计算得到的刚性墙速度、位移数据，计算不同模型下响应数据的差方和SSD，SSD计算方法为

( 4 )

式中：i为曲线上数据点编号；n为曲线上数据点的数量；Ti为第i个数据点的输出时间；Kl为刚度曲线上第l个离散值；Cm为阻尼曲线上第m个离散值；Yi为响应指标目标值。

在图2曲线上取10 个内点，将纵坐标值解析为设计变量；参考文献[23]中求得的阻尼曲线变化趋势，为车体假设一条初始阻尼曲线，速度范围为0～10 m/s，在曲线上取10 个内点并将其定为设计变量。

车体等效参数反演优化问题的数学描述为

minSSD

s.t. 0≤Kl≤12 000l=1,2,…,10

0≤Cm≤12 000m=1,2,…,10

( 5 )

这里选择车体冲击过程中刚性墙的动态响应作为反求简化单车模型参数问题的目标，主要有位移和速度2个参量。单车简化模型中的刚度、阻尼参数校正前后与实际模型计算的刚性墙的速度位移曲线对比见图4。对Tc车来说，参数校正后的简化模型计算所得的刚性墙响应曲线与实际模型计算的响应曲线拟合效果比较理想，但是M车的参数校正后简化模型计算的响应曲线与实际模型存在一定偏差，尤其以速度曲线差异明显。说明用非线性杆元模拟车体的受冲击行为时，Tc 车的等效模拟结果要优于M车，仅以冲击物的响应作为目标不足以更好地表征车体受冲击时的响应特征，尤其是对于M车。

4 结果讨论

4.1 指标选择对校正结果影响

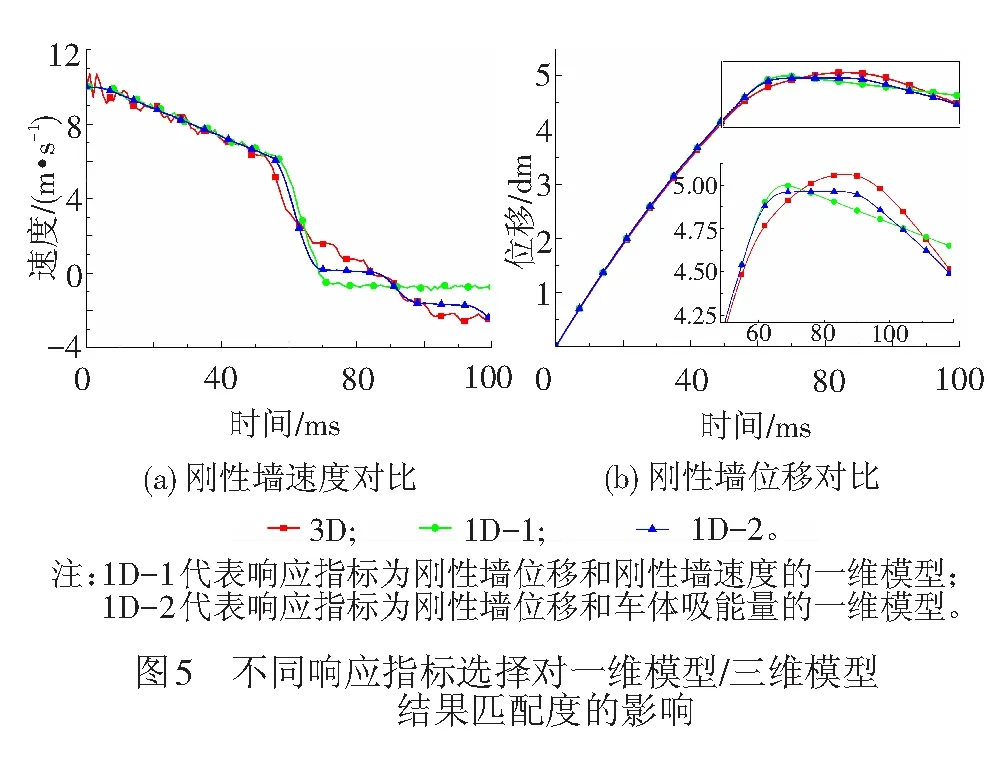
M车的校正效果欠佳，在速度衰减段与真实三维模型计算情况偏差较大。为了验证这种情况是否因为参数校正问题中目标选取不同所致，对参数校正指标进行了重新确定。参考以往的整列编组列车耐撞性分析数据，车体结构在碰撞过程中存在一定的能量吸收，考虑车体自身内部响应指标是否可以提高参数校正后一维模型响应与三维模型响应的匹配度？基于这种考虑，针对M车的一维模型参数校正问题，重新定义了匹配目标，既考虑了外部刚性墙的响应，又加入了车体结构的能量吸收。选择不同响应优化得到的校正结果对比见图5情况。从图5(a)中可以看出，在目标响应中加入车体能量指标时，一维模型计算的结果更接近实际三维模型结果，特别是从60 ms开始对应的减速段，一维模型计算的速度曲线表现出了持续衰减特征，单车的一维模型与三维模型计算的刚性墙速度趋势匹配度得到改善。图5(b)为采取不同指标时刚性墙位移变化曲线对比情况，考虑车体吸收能量后，位移曲线与三维模型中刚性墙位移走势更接近，峰值误差控制在5%内，相比三维模型，一维模型计算所得的刚性墙位移峰值出现时刻略提前25 ms。

4.2 不同算法对校正结果影响

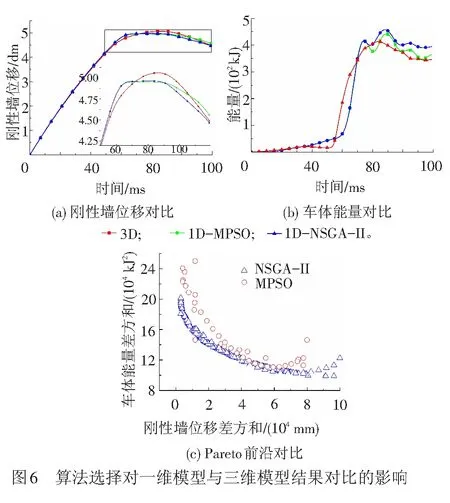
为了测试不同的优化算法得到的参数对一维模型计算结果的影响，以车体能量与刚性墙位移作为目标响应，分别采用NSGA-Ⅱ遗传算法和多目标粒子群算法(MPSO)对单车车体简化单元进行参数校正，见图6(a)所示。不管是采用NSGA-Ⅱ遗传算法还是多目标粒子群算法得到的校正参数，一维模型计算得到的刚性墙位移变化与三维模型基本一致，误差控制在5%以内。但是对于车体吸收能量，采用NSGA-Ⅱ算法得到的校正参数时，一维模型计算得到的数据更为接近三维模型计算结果，多目标粒子群算法次之，见图6(b)，在50～80 ms上升段，校正后的一维模型在能量吸收上表现出较为明显的滞后，而且能量达到稳定值所需时间比实际三维模型小，达到稳定值后能量有轻微震荡。这也反映出一维模型中响应信息纵向传播过程要快于实际三维模型，由于结构的本身差异，这种响应传播差异无法消除。图6(c)给出了两种算法得到的多目标最优解Pareto前沿，在一维模型的参数校正问题中，优化计算量相当的情况下，从得到的最优解数量和解的均布性方面来看，NSGA-Ⅱ算法显然优于粒子群算法。

5 简化模型验证

由图4和图5给出的对比结果表明，在刚性墙冲击单车工况中，单节车体的一维模型与三维模型计算得到的刚性墙速度与位移吻合较好。但是对比响应局限于刚性墙本身，由于未考虑车体自身响应，所以有必要进行一维模型代替三维模型分析可行性的进一步验证。通过对比车体单元吸能、车体纵向变形量进一步验证Tc车和M车一维模型准确性。从前面的响应指标对模型计算结果影响来看，采用车体吸收能量和刚性墙位移作为指标得到的一维模型校正结果具有较好精度，这里采用1D-2一维模型，将分析结果与对应的三维模型计算结果对比，考虑到在冲击过程中的车体的响应数据波动，这里延长了冲击求解时间，Tc车为350 ms，M车为250 ms。

简化车体模型和三维模型计算的车体单元吸能和车体纵向变形量对比见图7。车体在纵向冲击载荷下，应力波对车体造成多次加载与卸载，车体纵向变形呈现出明显的波动，波动段曲线平均值即为车体的残留塑性变形。总体来看，一维模型计算得到的纵向变形曲线波动比三维模型更为明显，能量曲线也出现相同的变化规律。Tc车的一维模型计算的能量曲线在175～200 ms范围内出现明显的峰值，随后回落至平稳波动状态，这种现象是由前端中心车钩剪切后空行程结束车体瞬时承载所致。M车车钩未设置剪切，车体承载过程不发生间断，未出现能量曲线剧烈波动。

由图7(a)可见，一维模型计算的能量吸收曲线与车体纵向变形曲线与三维计算模型的趋势基本一致，数值吻合度较好。由图7(b)可见，M车的能量吸收达到峰值后出现小幅波动。

Tc车和M车的一维模型和三维模型计算的车体能量吸收与纵向车体变形量见表1，其中M车的一维模型计算纵向变形误差为8.42%，能量误差9.83%，计算误差高于Tc车，两车的数据误差均不超过20%，计算误差在工程应用接受范围之内。

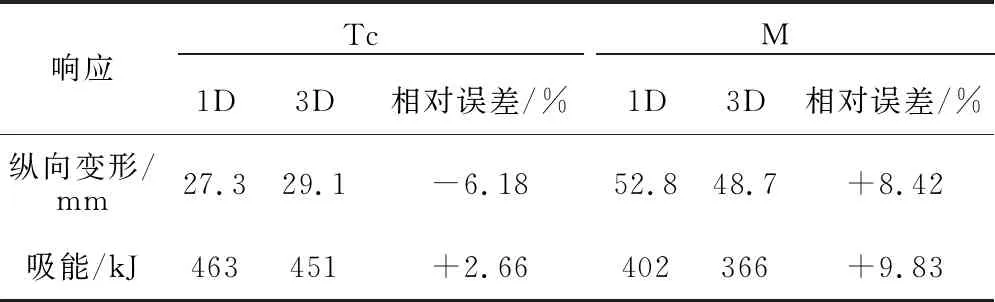
表1 一维模型与三维模型响应对比

6 算例

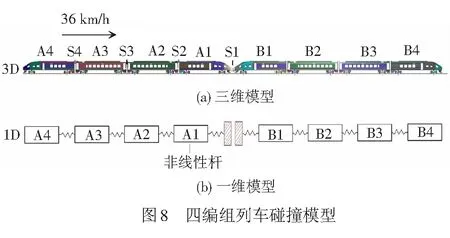
为了验证单车参数在整列编组模型中的适用性，这里建立了四编组列车对撞的一维模型，建立并求解了三维四编组有限元对撞模型与一维模型进行数据对比。

用于列车对撞分析的三维有限元模型包含单元总数为6 920 489，节点总数为6 067 564，其中包括105 个弹簧单元和刚性单元, 6 678 670个壳单元，241 714个实体单元。计算模型求解在HP Z840 Workstation(CPU E5-2670，2.3 GHz，RAM 64 GB)上进行，模型求解时间1 000 ms，CPU耗费机时101 h，计算模型文件大小886 MB, 输出间隔为60 ms，仿真计算完成后产生11.14 GB的数据文件。

按照实际的列车编组信息，建立了与实际编组模型对应的一维模型，见图8。其中车体的纵向特征由非线性杆元表征，刚度与阻尼参数取校正后的数值。采用非线性弹簧阻尼单元模拟车钩的吸能行为。

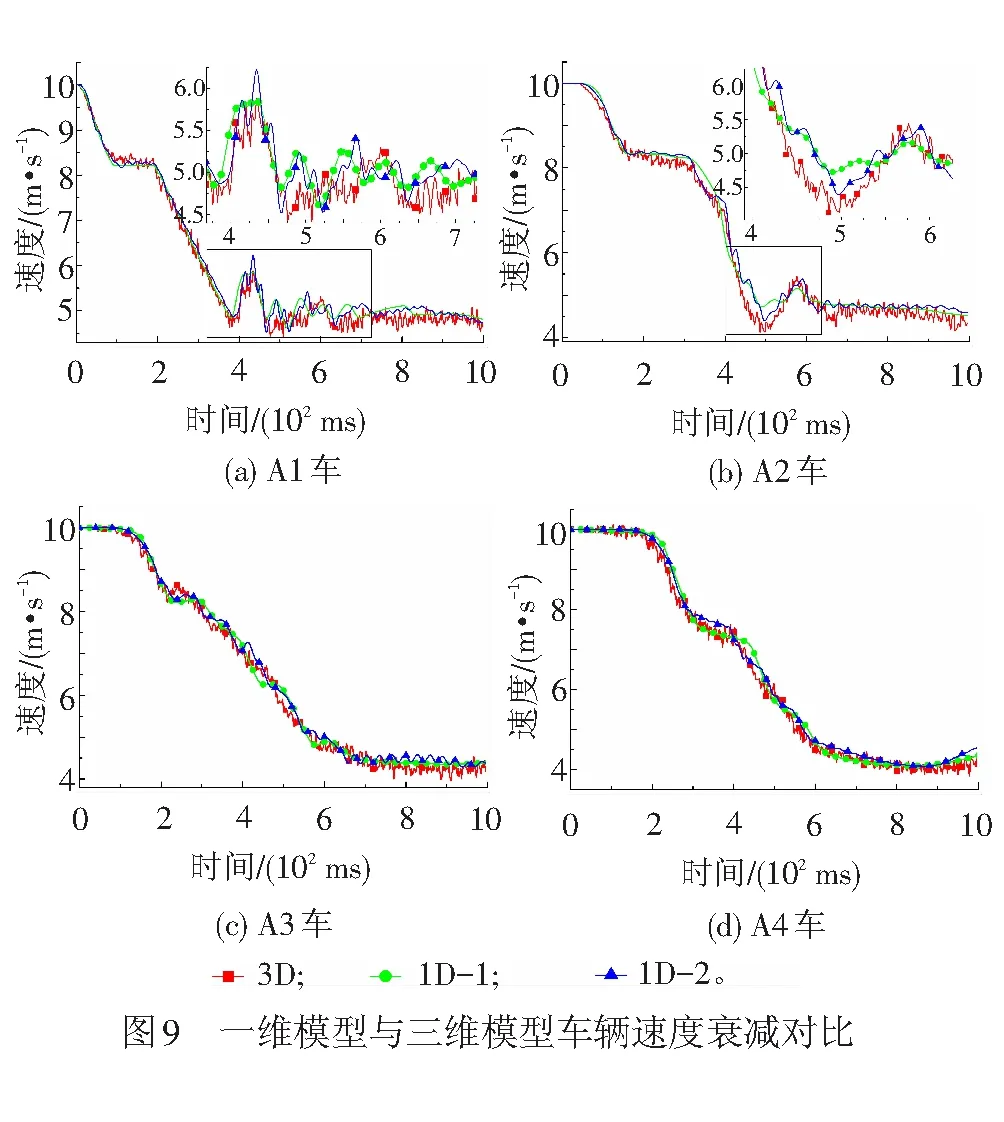
为了验证车体杆元的校正参数对于编组列车纵向碰撞响应的预测情况，分别采用三维模型与一维模型进行36 km/h碰撞工况下的碰撞分析，提取了各个车辆的纵向速度时程数据并进行结果对比。两种一维模型和三维模型计算得到的运动列车各车辆在对撞工况下的速度衰减曲线见图9。A1车和A2车由于车端车钩吸能元件发生完全压溃，速度在5 m/s附近出现多次震荡，车体在此时受到的冲击载荷较大，一维模型与三维模型的速度衰减曲线匹配程度也反映了车体简化单元是否较好地表征车体的纵向特性。相比三维模型计算结果，两种一维模型计算的A1车的速度在460～700 ms区段内均有提前，A2车的速度在500 ms左右，显示了两种一维模型的明显差异，一维模型对应的速度震荡与三维结果更为接近。A3车和A4车中一维模型与三维模型计算得到的速度衰减曲线走势基本一致，这主要是由于A3、A4车两端的车钩尚未完全压溃，车体承受的最大载荷即为车钩稳态压溃载荷，车体承受冲击作用要显著小于A1车和A2车。

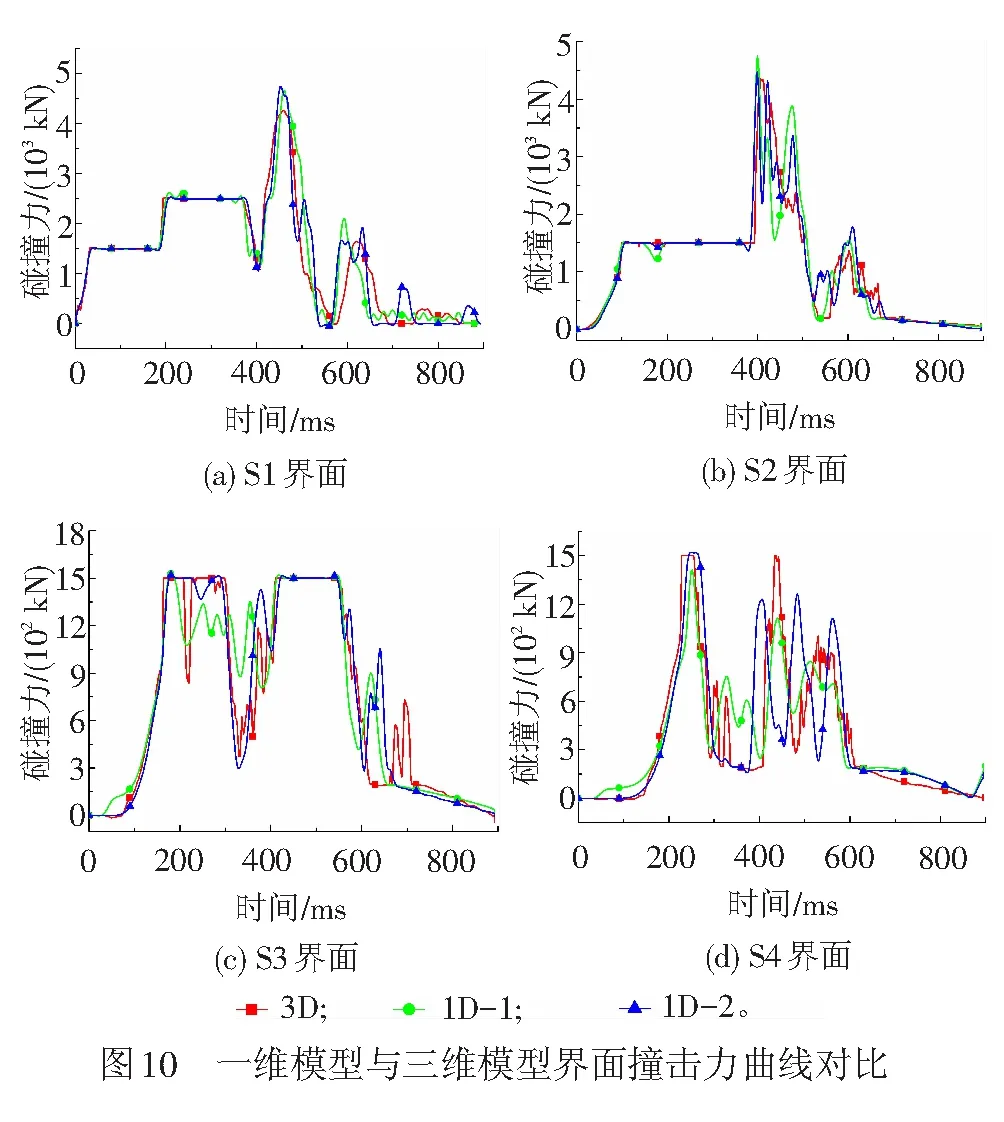
两种一维模型和三维模型计算所得到的列车连挂界面S1-S4(见图8)车钩力变化曲线对比见图10。S1和S2处的车钩达到满行程后随即出现了较大的峰值力，截止碰撞过程结束，S3和S4界面处车钩仍有剩余行程，界面力峰值未超过车钩稳态压溃载荷。显然，在车钩完全压溃的界面S1、S2处，1D-2模型对应的车钩力与三维模型计算结果吻合程度要优于1D-1模型，在车钩未完全压溃界面S3、S4处，1D-2模型计算结果也要比1D-1模型接近三维模型计算结果。

两种一维模型预测的峰值力差异不大，车钩完全压溃界面S1和S2处不同模型计算的界面力峰值对比情况见表2，1D-2模型计算的S1界面力峰值误差为11.31%，略高于1D-1的9.64%，而对应的S2界面峰值力相对误差明显小于1D-1。

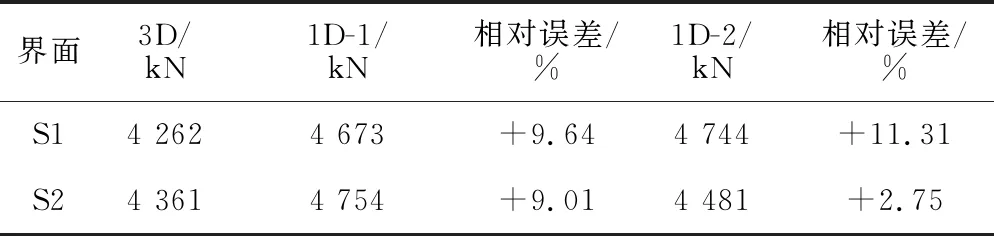
表2 不同模型计算界面力峰值对比

7 结论

本文建立了一种基于非线性杆元的列车碰撞一维模型，并通过参数校正的方法获取了简化单车模型中车体的等效参数，最后将单车一维模型推广至列车碰撞模型，并采用编组算例验证了其可行性，得出以下结论：

(1) 通过非线性单元来表征车体在纵向冲击载荷下的响应是可行的，但是需要对简化单元进行参数校正，校正后的一维模型可用于列车耐撞性方案前期设计评估和选优。

(2) 单车的一维模型校正中，在优化计算量相当的情况下，推荐采用NSGA-Ⅱ算法，可以获得较多的最优解和分布均匀的Pareto前沿，可供最优解选取和方案决策。

(3) 在一维模型参数校正的指标选择上，兼顾车体本身的内部响应和外部响应能获得较好的等效参数，一维模型与三维模型匹配度较好。