考虑川藏铁路控制性工程的甲供物资基地选址决策方法

张 锦， 徐君翔， 郭静妮， 唐秋宇

(1. 西南交通大学 交通运输与物流学院， 四川 成都 610031；2. 西南交通大学 综合交通大数据应用技术国家工程实验室， 四川 成都 610031)

川藏铁路的规划和建设是助推交通强国、交通强省战略实施的国家重大任务之一。铁路线路起于四川省成都市，经雅安、康定、昌都、林芝至西藏拉萨，线路全长1 838 km，预计建设总工期为12年[1]。川藏铁路沿线具有板块运动活跃、地质灾害频繁、气候条件恶劣等特点，线路“穿七江过八山”，桥梁结构复杂、超长深埋隧道众多，川藏铁路雅林段的桥隧比高达92.6%，工程建设中的物资保障面临巨大挑战[2]。2019年即将启动的大渡河特大桥、折多山隧道、怒江大桥和易贡隧道作为川藏铁路雅林段“两桥两隧”控制性工程，预计整个工期为10年，因此有必要研究适用于川藏铁路工程建设的甲供物资基地选址模型与选址决策的方法，解决物资供给问题。关于选址问题国内外的许多专家学者很早就开始研究，主要从无备选址和有备选址两方面研究。无备选址方面，主要考虑改进模型与算法研究各类问题的选址布局及优化，以优化选址策略、提高选址效率和选址精确合理性。通过采用遗传算法、蚁群算法、禁忌搜索算法、聚类分析、神经网络模型、深度学习算法等方法[3-7]，解决物流节点、电动车充电桩、医疗设施、客货运车站等实际问题的选址优化问题[8-9]。有备选址方面，主要针对不同实际问题，考虑多属性多准则因素，对各类实际问题的选址方案进行评价和决策，通过采用模糊理论、二元语义群决策法、灰色关联分析、前景理论、证据理论等方法[10-12]，解决配送中心、应急救援中心等公共服务设施的选址方案综合评估与精准决策的问题[13-15]。虽然目前在选址问题研究的理论与方法上取得了许多成果，研究成果在实际问题中也得到了应用，但是面对物资需求不确定性大、施工交通组织困难、工程环境艰险复杂的川藏铁路工程中的甲供物资基地选址问题，现有的理论与方法不足以支撑研究[16]。

川藏铁路雅林段2019年开工“两桥两隧”控制性工程，工程特征为建设周期长、施工难度大、施工技术要求高，对川藏铁路雅林段整个工程项目推进具有重大影响，因此如何在保障控制性工程建设能顺利推进的同时满足将来铁路沿线其他工程项目的甲供物资供给需求，亟待研究科学合理的选址方法。本文研究拟假设有备选址情景下的工程建设甲供物资基地选址决策问题，创新之处在于选址决策针对川藏铁路“两桥两隧”控制性工程的建设特征、建设周期、建设环境、长远战略等，从决策者决策心理行为角度出发改进传统前景理论，将决策行为考虑为冒险型、保守型和中间型，定义基于直觉模糊交叉熵的新记分函数，并定义组合赋权模型，利用各选址决策方案的综合前景值大小对比得到最优选址方案。

1 直觉模糊集和记分函数

定义[17]假设X是一个给定的论域，则X上的一个直觉模糊集A可记为

A={〈x,μA(x),θA(x)〉|x∈X}

式中：μA(x)、θA(x)分别为论域X中的元素x属于A的隶属度和非隶属度，且有μA(x)∈[0,1],θA(x)∈[0,1],0≤μA(x)+θA(x)≤1。

πA(x)为x对A的犹豫度。

πA(x)=1-μA(x)-θA(x)

为了方便起见，直觉模糊集也可以表示为A=〈μA(x),θA(x),πA(x)〉。在一个直觉模糊集A中，其隶属度μA(x)、非隶属度θA(x)和犹豫度πA(x)表示对于任一元素x属于直觉模糊集A的支持、反对和中立3种态度的程度。记分函数S(A)是用函数关系将直觉模糊数转化成具体数值来确定模糊集排序关系的一种排序思路，最早是由Chen等[18]于1994年定义

S(A)=μA(x)-σA(x)

式中：σA(x)为非隶属度，与定义中的θA(x)含义相同。该记分函数表示的直觉模糊数隶属度与非隶属度的差值，差值越大，直觉模糊数越大，但是此记分函数忽略了犹豫度πA(x)对决策的影响，当两个直觉模糊数差值相同，但是隶属度和非隶属度不同的情况下将难以比较大小。

Hong等[19]定义直觉模糊数的精确函数C(A)为

C(A)=μA(x)+σA(x)

C(A)值越大说明方案的已知信息越多，方案就越优。但是精确函数必须与得分函数同时使用才能得到直觉模糊数的大小。

Ye[20]将犹豫度考虑到记分函数中，利用参数λ来反映犹豫度πA(x)的作用，他提出的改进记分函数为

S(A)=μA(x)-σA(x)+λπA(x)

λ∈[0,1]，但是其值的确定很难找到合理的依据，因此也不能通过该记分函数科学合理反映直觉模糊数的大小。

王坚强等[21]综合考虑了直觉模糊集中的隶属度、非隶属度和犹豫度对决策结果的影响，提出了用直觉模糊交叉熵来定义记分函数。

S(A)=

式中：H(x)为直觉模糊交叉熵。

该记分函数S(A)综合考虑了隶属度和非隶属度的交互关系来确定犹豫度的大小，但是如果隶属度和非隶属度相同的情况下，就不能用记分函数来比较，需要进一步考虑。

由于本文考虑基于前景理论的决策方法是建立在决策者非理性心理的基础上的，以上的不同记分函数定义方法考虑层面各有侧重，但都未引入决策者的心理行为，因此均不适合用于本文的研究，针对本文实际研究背景需要重新构造记分函数。

2 基于改进前景理论的直觉模糊多属性决策方法

2.1 新的记分函数

直觉模糊交叉熵可以运用隶属度与非隶属的交互关系来确定犹豫度，从而优化当隶属度、非隶属度和犹豫度之间信息不确定的情况下，记分函数构造的缺陷问题，但是会导致直觉模糊集中的隶属度与非隶属度相同情况下需要进行二次比较的问题。因此本文的研究考虑才用直觉模糊交叉熵并引入指数函数的形式构造新的记分函数。定义：假设任意直觉模糊集A=〈μA(x),θA(x),πA(x)〉，则直觉模糊集A的记分函数为

( 1 )

( 2 )

( 3 )

( 4 )

新的记分函数利用直觉模糊交叉熵解释了原来记分函数中犹豫度、隶属度和非隶属三者之间的关系依据，并改进了基于直觉模糊交叉熵改进记分函数之后由于隶属度和非隶属度相等情况下，需要进行二次比较的问题，若在此记分函数中出现μA(x)=θA(x)，则有

( 5 )

2.2 改进前景理论

Kahneman等[22]通过大量的心理行为实验于1979年提出了前景理论。前景理论由价值函数和概率权重函数共同组成，即

V=h(p)u(q)

( 6 )

( 7 )

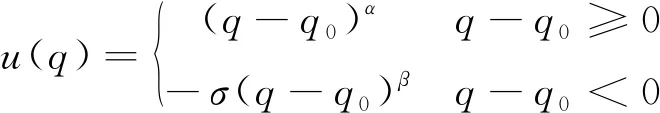
( 8 )

式中：V为前景价值；h(p)为概率权重函数；u(q)为价值函数；χ为风险收益态度系数，0<χ<1；δ为风险损失态度系数，0<δ<1；h+(p)为收益权重函数；h-(p)为损失权重函数；q-q0为决策方案相对于参考点的差异值，当q-q0≥0时，u(q)为收益值，当q-q0<0时，u(q)为损失值；α和β为风险态度系数，0<α<1，0<β<1；σ为损失规避系数，σ越大则决策者对损失的敏感度越高。

由于决策者在做决策时存在不同的决策偏好，决策者按性格类型可分为冒险型、中间型和保守型，考虑通过改进传统前景理论模型来刻画人们在面对损失和收益情况时不同心理表现，即损失厌恶心理。因此通过改进传统前景理论模型中的价值函数和概率权重函数来定义的新模型表现形式为

( 9 )

(10)

(11)

2.3 权重计算方法

目前关于指标权重确定方法分为主观赋权法和客观赋权法，主观赋权法主要是根据决策者的经验判断来赋予权重，不考虑评价指标的内部关联情况，常见的有专家评判法和层次分析法(AHP)；客观赋权法主要通过定量分析，考虑指标之间的内在联系，客观赋予权重，但是忽略了决策者的经验偏好等，常见的有粗糙集赋权法、相关系数法和熵值法。因此，为了使指标的权重值具有实际性和准确性，从而适用于对本文实际应用背景下的决策研究，考虑采用主观赋权法和客观赋权法相结合的主客观赋权法来确定决策指标的权重。

G1法是在传统的AHP法进行改进基础上提出的一种主观赋权法，不仅能够满足一致性检验的要求，还能避免了AHP法中计算量大、计算过程多、结果精度不高的缺点，适用于同一层级的指标权重计算。采用G1法进行指标权重计算的步骤见图2。

Step1数据标准化处理

由于在风险预警指标中的量纲和数量级均存在差异，因此需要消除因量纲不同对评价结果产生的影响，首先对指标进行标准化处理。

(12)

Step2确定信息熵值和信息效用值

指标的信息效用值Ii取决于该指标的信息熵Ei与1之间的差值，差值越大则信息效用值越大，权重也就越大。

(13)

(14)

Ii=1-Ei

(15)

Step3确定各决策指标的权重值

熵值法求指标的权重值就是利用该指标的信息价值Gi进行计算，其值越高对评价的重要性就越大。

(16)

(17)

假设由主客观赋权法求得的权重值为W1i和W2i，A和B分别表示G1法和熵值法的相对重要程度，A+B=1，则主客观赋权的权重值Wi为

Wi=AW1i+BW2i

(18)

2.4 方案决策步骤

基于改进前景理论的直觉模糊多属性决策方法步骤如下：

Step3确定指标权重。根据式(18)计算各决策指标的组合权重值，记为

W={w1,w2,…,wn}

Step4计算各类型决策偏好下各备选方案的综合前景值，完成不同偏好下的决策方案的排序。根据

j=1,2,…,mi=1,2,…,n

(19)

可以计算出各决策方案的综合改进前景值，若综合改进前景值Ui越大则对应的方案就越优。

3 川藏铁路控制性工程建设中的选址决策

本文重点研究的是川藏铁路雅安至林芝段的工程建设中的甲供物资基地选址问题，根据在川藏铁路雅安至林芝段上的“两桥两隧”控制性建设工程特征，结合川藏铁路雅林段上的沿线重点难点工程布局，考虑有拟备选址的情况下采用基于改进前景理论的直觉模糊多属性决策方案实现甲供物资基地选址方案决策。川藏铁路雅林段的“两桥两隧”工程建设特征见表1，川藏铁路雅林段沿线重难点工程布局概况见图3。

表1 “两桥两隧”控制性工程建设特征

3.1 考虑“两桥两隧”控制性工程建设拟备选址分析

由川藏铁路沿线重点难点工程布局图和川藏铁路控制性工程建设特征可知，川藏铁路雅林段的大渡河特大桥工程和折多山隧道工程靠近雅安康定，易贡隧道和怒江特大桥靠近波密林芝，因此可基于控制性工程的分布拟考虑修建2个甲供物资基地，从近期看可服务于雅林段控制性工程建设物资供给保障，从远期看可服务于雅林段之间的其他桥隧工程建设物资供给保障。雅林段拟备选址假设为泸定、康定、雅江、理塘、白玉、江达、昌都、邦达、八宿、波密和林芝11个地点，由于蒲江已规划有物流中心，因此不考虑在雅安规划物资供给基地。这11个备选址都是川藏铁路沿线必经的地点，具体的铁路车站选址位置还未确定，这11个备选址依次位于四川盆地、川西高山峡谷区、川西高山原区、藏东南横断山区、藏南谷底区等5个地貌单元，区域山高谷深、地形条件极其复杂、地质灾害频繁，跨越14条江河和21座4 000 m以上的雪山，川藏铁路工程在这11个地方建设的沿线桥梁隧道比例为86%，其中雅安至林芝段的桥隧比高达92.6%。

全面综合客观地考虑川藏铁路雅林段控制性工程以及沿线重难点工程的甲供物资基地选址决策影响指标和因素，顺利保障川藏铁路工程建设的开展和提高物资运输效率。通过归纳梳理大量文献，结合川藏铁路工程建设的实际环境，并综合相关领域专家意见，最终确定了决定“两桥两隧”工程建设中的甲供物资基地选址的12项指标，将其整合成了6项指标(c1～c6)，见图4。

3.2 基于改进前景理论的直觉模糊多属性决策下的选址结果

某施工单位考虑依托川藏铁路“两桥两隧”控制性工程计划在川藏铁路雅林段选址修建2个大型甲供物资供给基地，现有11个备选方案，3.1节中已列出。在决策这11个备选方案时需要考虑6项指标，分别是交通运输c1，地质条件c2，气候环境c3，选址特征c4，工程建设c5和通讯条件c6。由于川藏铁路沿线施工环境极其复杂，施工作业受气候条件影响极大，因此可以将决策方案分为春季选址决策方案(P1)，夏季选址决策方案(P2)，秋季选址决策方案(P3)和冬季选址决策方案(P4)，其概率影响经专家评估依次是0.35，0.20,0.30,0.15(4个季节的概率大小是笔者通过参与设计院和工程院召开关于川藏铁路工程建设相关省部级重大课题得到的模糊评估值)。直觉模糊决策矩阵经专家打分得到，专家的可信度标准从专家的工龄、学历、专业、经历、职称5个方面来评判，具体标准权重见表2。直觉模糊决策矩阵见表3～表6。

表2 专家评分权重标准

专家可信度的计算式为

(20)

表3 春季选址直觉模糊决策矩阵S1

表4 夏季选址直觉模糊决策矩阵S2

表5 秋季选址直觉模糊决策矩阵S3

表6 冬季选址直觉模糊决策矩阵S4

D1=

D2=

D3=

D4=

(1) 若决策者为冒险型，则0<α<1,0<β<1，令α=β=0.5，χ=δ=0.6，σ=1,λ=2.5，得到的改进前景决策矩阵为

V1=

(2) 若决策者为保守型，则α>1,β>1，令α=β=2.5，χ=δ=0.6，λ=1,σ=2.5，得到的改进前景决策矩阵为

V2=

(3) 若决策者为中间型，则α=β=1，χ=δ=0.6，λ=σ=1，得到改进前景决策矩阵为

V3=

Step3根据式(18)得到指标ci的权重值为w1=0.252,w2=0.256,w3=0.168,w4=0.044,w5=0.128,w6=0.152。

Step4根据式(19)得到方案的综合前景值结果见表7。

表7 不同决策偏好下的综合前景值结果

由不同决策偏好下的综合前景值结果可知，若决策者为冒险型，则最佳选址方案为康定和波密；若决策者为中间型，则最佳选址方案为林芝和康定；若决策者为保守型，则最佳选址方案为林芝和泸定。不同偏好下的决策结果见图5。由于川藏铁路雅林段的工程建设复杂，桥隧工程项目众多，控制性工程所处建设位置处于复杂艰险高原高寒山区，为了保障整个工程顺利推动实施，支撑川藏铁路建设中后续重大工程的开展，笔者建议甲供物资基地选址采用保守型的选址结果，建议相关决策者选择林芝和泸定两个地方作为甲供物资基地，林芝和泸定两个地方从施工环境、气候条件、地质构造等多方面考虑都是最符合目前选址条件。

4 结论

川藏铁路雅安至林芝段工程建设从“两桥两隧”控制性工程动工开始，保障控制性工程的顺利推动对整个工程建设的影响至关重要。本文的研究是考虑面向川藏铁路控制性工程建设的拟备选址情景下，甲供物资基地选址决策问题，从决策者的决策心理行为出发改进了传统的前景理论价值函数和概率权重函数，并提出了一种新的记分函数，通过组合赋权法确定了决策指标的权重，构建基于决策者不同决策偏好下的改进的综合前景决策矩阵，通过对比综合前景值得出不同决策偏好下的最优选址方案。本文的研究将前景理论应用到了实际工程问题中，同时也也为直觉模糊多属性决策方法提供了一种新的思路，还为推动川藏铁路工程建设起到重要支撑作用。未来还可以继续深入研究不同决策方法在川藏铁路工程建设中的甲供物资基地选址中的应用，考虑用各种决策方法的对比得到的选址方案，体现选址方法在不同情境中的适用性。