二维调和分数阶扩散方程的数值模拟
陈景华,陈雪娟,章红梅
(1.集美大学理学院,福建 厦门 361021;2.福州大学数学与计算机科学学院,福建 福州 350108)
分数阶导数可模拟物理领域中的许多问题[1-5],与离散随机游走过程联系紧密[6]. 一个阶数α(α<2)的空间分数阶导数可模拟具有长尾幂律性态的粒子跳跃,其跳跃步长的分布为P[J>x]≈x-α,而一个阶数β<1的时间分数阶导数可模拟长尾幂律性态粒子的跳跃,其两次跳跃的等候时间为P[W>t]≈t-β.本文中我们关注的是调和分数计算,其分数阶导数是通常的分数阶导数乘上一个指数因子的卷积核.这个调和分数阶导数可模拟调和的指数幂律,粒子的跳跃长度为P[J>x]≈x-αe-λx[7-8]. 调和扩散方程已广泛应用于地球物理[9-12]和金融[13-14]等领域.在金融领域里,调和稳定的过程可模拟具有半长尾性态的价格截断.近年来关于分数阶数值方法已有不少的成果[15-22],但是关于调和分数阶扩散方程的数值方法还比较少.Sabzikar 等[23]给出一个调和分数阶差分格式求解调和分数阶扩散方程.Baeumer等[24]给出粒子追踪法和差分法来求解具有漂流项的调和分数阶方程.Zhang等[25]发展了一个新的数值算法求解Riesz调和空间分数阶扩散方程.以上所考虑的方程都是一维调和分数阶方程. 本文中考虑二维调和分数阶方程,采用隐式交替方向法(ADI)和Crank-Nicolson(C-N)离散格式求解二维调和分数阶方程,并证明所给出的差分格式是无条件稳定和收敛的.
1 数值离散
Podlubny等[26]给出了左侧和右侧Riemann-Liouville (R-L)分数阶导数的定义:
这里u(x)定义在[a,b]区间,1<α≤2,Γ(·)是Gamma函数.
在此基础上给出α阶左侧和右侧的R-L标准调和分数阶导数的定义[23-24].
定义1如果u(x)∈[a,b],则∀λ≥0,α阶左侧和右侧R-L标准调和分数阶导数的定义分别用式(1)和(2)表示:
(1)
(2)
这里1<α≤2.

本文中考虑如下具有左侧R-L标准调和分数阶导数的二维扩散方程:
(x,y)∈Ω=(xL,xR)×(yL,yR),
0≤t≤T.
(3)
其中:1<α≤2,1<β≤2; 扩散系数:d(x,y)>0,e(x,y)>0;q(x,y,t)是源项. 方程(3)可模拟长时间随机游走极限,其平面跳跃的随机点(X,Y)坐标的分布为:P[X>x]≈x-αe-λ1x和P[Y>y]≈y-βe-λ2y,且X,Y是相互独立的. 假设这个分数阶扩散方程(3)在以下初始和边界条件下有光滑的唯一解,并设初始条件为:
u(x,y,0)=f(x,y),(x,y)∈Ω,
(4)
Dirichlet边界条件为:
u(x,y,t)=B(x,y,t),(x,y)∈∂Ω,
0≤t≤T.
(5)
这里加上一个限制条件B(xL,y,t)=B(x,yL,t)=0. 这个条件的设置是有实际意义的:可以设想平面区域足够大时,溶质在地下水层的扩散,在左边界和下边界浓度为0.
注2如果方程(3)中α=β=2,λ=0,则二维调和分数阶扩散方程就退化成经典的二维扩散方程.
接下来采用左移位的Grünwald估计和ADI,建立方程(3)的二阶C-N格式.
引理1[24]设1<α≤2,f∈Wn+3,1(R),n是整数且n≥1.设p∈R,h>0,λ≥0.定义左移位的 Grünwald-Letnikov(G-L)调和算子:
这里h是空间步长,权重系数为
则∀x∈R存在不依赖于h、f、x和λ的常数aj使得:
O(hn).
αλα-1f′(xj)+O(h),
(6)
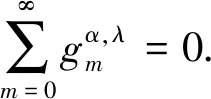


(7)
这里
(8)
(9)
方程(10)可写成算子的形式:
0≤i≤Nx,0≤j≤Ny,
n=0,1,…,N-1.
(11)

(12)
(13)
(14)
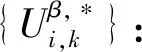
(15)

(16)
以下是求解式(15)、(16)的具体步骤. 首先将式(15)展开写成:
i=1,2,…,Nx-1,
固定j=k(k=1,2,…,Ny-1).
(17)
从式(17)可以得到一个Nx-1个的线性方程,这里第i个方程表示如下
i=1,2,…,Nx-1.
系数Ai,m,(i=1,2,…,Nx-1,m=0,1,…,i+1) 定义如下:
小儿脏腑柔弱,气血未充,腠理不固,易为外邪侵袭。外感时邪,正邪相搏而致外感发热。热极易生风,加之小儿肝常有余,肝风内动易致惊风。风性善行而数变,故小儿病情发展变化迅速,合并症多,应尽快予以诊治,以免贻误病情。根据中医“异病同治”的治疗原则,由各种不同疾病引起的发热经中医辨证论治后都可选用相应的中成药物治疗。而西医多采用静脉给予抗感染抗病毒药物,同时给予口服退热药或冰袋物理降温等治疗,虽亦有效,但因小儿畏惧打针吃药,往往不配合医护人员的操作,增加了治疗难度,而选择热毒宁注射液灌肠则为临床医护人员提供了方便,减轻患儿的痛苦。
Ai,m=
(18)
系数Bi,m(i=1,2,…,Nx-1,m=0,1,…,k+1)定义如下:
Bi,m=
(19)
类似的,固定i=k(k=1,2,…,Nx-1),j=1,2,…,Ny-1,把方程 (16)重新写为:
(20)
因此上述的方程组就是求解Ny-1个线性方程,在(xk,yj)处,第j个方程形式如下:
j=1,2,…,Ny-1,
这里系数
m=0,1,…,j+1) 分别定义如下
(21)
(22)
2 稳定性和收敛性证明
这一节,证明方程(3)的差分格式(10)是相容且无条件稳定的,因此是收敛的.
证明这个证明类似文献[27]. 主要的差别是Grünwald 权重系数由调和加权系数来替换。

定理2方程(3)的差分格式(10)是无条件稳定的.
证明主要采用圆盘定理和矩阵的特征值来证明稳定性.
方程(12)可写成矩阵的形式
(I-S)(I-T)Un+1=(I+S)(I+T)Un+Rn+1,

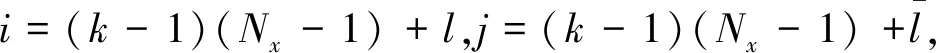
si,j=
(23)
注意到
容易计算得到
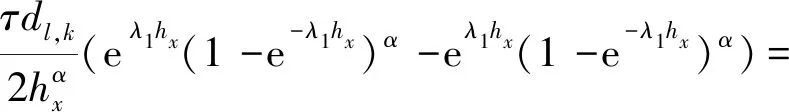
0,
(24)

3 数值例子
这节考虑平面矩形区域Ω=(0,1)×(0,1)上的二维调和分数阶扩散方程

q(x,y,t)=
(25)
初始条件参数设置为λ1=λ2=0.5,α=β=1.7,k1=k2=3,
边界条件为
u(0,y,t)=0,
u(x,0,t)=0,
精确解为
同时取误差范数为最大误差:

表1给出了外推前的最大误差、误差率和外推后的最大误差、误差率的比较. 可以观察到外推前的误差率接近:
外推后的误差率接近:


表1 外推前后最大误差、误差率的比较
4 结 论
本文中发展了一个分数阶交替迭代法并结合C-N格式和Richardson外推法数值模拟二维调和分数阶扩散方程,采用矩阵分析方法结合圆盘定理证明差分格式的稳定性和收敛性. 此数值方法也可运用于非线性源项的高维调和分数阶反常扩散方程.

