八元数闭逐块光滑流形上的奇异积分
龚定东
(浙江理工大学理学院,浙江 杭州 310018)
八元数作为一种非交换非结合的代数,是一种特殊的Clifford代数,也是最大的除代数.关于八元数的函数论已有诸多学者作了研究[1-6],而且八元数的分析理论在科学技术领域中也有重要的应用[7].
在复分析中,Cauchy型积分及其奇异积分理论是一个十分丰富且极其重要的研究课题[8-12].对八元数而言,Li等[3]和Wang等[6]研究了八元数的积分表示.Wang等[6]讨论了八元数中具有光滑边界域上的奇异积分理论,进一步的研究还有待完善.受文献[8-10]中方法的启发,本文中利用八元数的Cauchy型积分研究奇异积分.
1 闭逐块光滑流形与八元数的Cauchy核
首先回顾一下八元数代数O的基础理论.八元数的单位元记为
e0,e1,e2,e3,e4,e5,e6,e7,其中e0=1.
八元数O中的任一元素x∈O可表示为
x=x0e0+x1e1+x2e2+x3e3+x4e4+x5e5+x6e6+x7e7,
其中xj∈R,j=0,1,…,7.
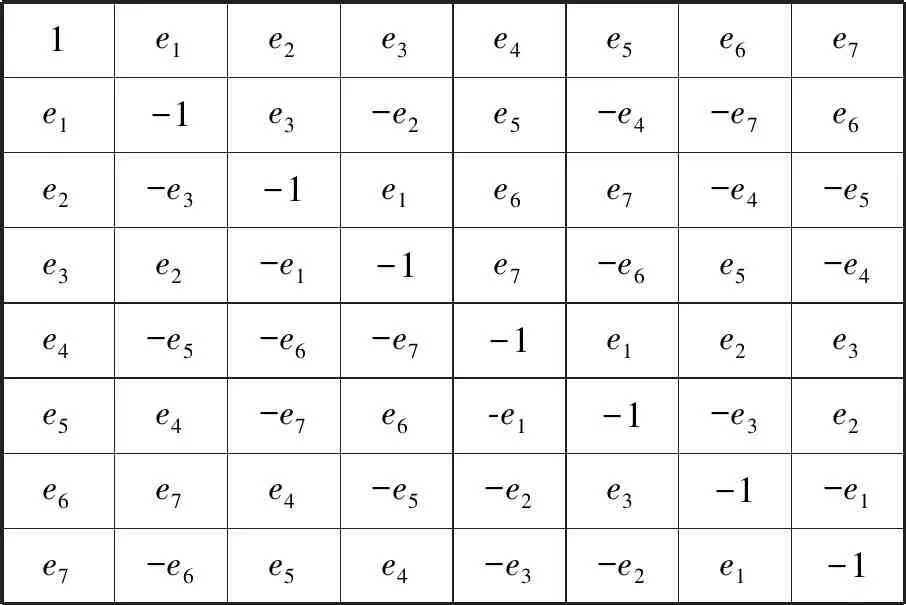
八元数中乘法满足如下的单位元基本乘法表(行乘以列)(见图1).
1e1e2e3e4e5e6e7e1-1e3-e2e5-e4-e7e6e2-e3-1e1e6e7-e4-e5e3e2-e1-1e7-e6e5-e4e4-e5-e6-e7-1e1e2e3e5e4-e7e6-e1-1-e3e2e6e7e4-e5-e2e3-1-e1e7-e6e5e4-e3-e2e1-1
图1 单位元基本乘法示意图
Fig.1 Diagram of the basic multiplication law of unit elements
另外,八元数中乘法还具有如下性质:
(i)eiej=ek,则ei+1ej+1=ek+1,
(ii)eiej=ek,则e2ie2j=e2k.

gj:Uj→R,1≤j≤k,
使得
(i)D∩U={u∈U|对1≤j≤k或者u∈Uj,或者gj(u)<0};

对{1,2,…,k}的每一个有序子集J={j1,j2,…,jl},‖J‖=l,定义
并选取SJ的定向使得在J的分量中是斜对称的.当给出D的通常定向时,则
记
Sj={u∈∂D∩Uj|gj(u)=0},
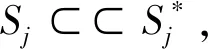
设
此处,ω8是R8中单位球面的曲面面积,Φ(x,z)为八元数O的Cauchy核函数[3].
定义一阶微分算子
函数f(x)称为是左(右)八元解析的,若
八元数O上也有类似于复分析中的Cauchy积分公式.
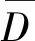
选择具有专业素养且口味互异的评价员20人,组成评价小组,对饮料的色泽、气味、口感进行评价。应用统计学的方法处理数据[9],所得感官评价方法如表1所示。
(1)
(2)
其中[Φ,Dfα,eα]=(ΦDfα)eα-Φ(Dfαeα)是八元数上的结合子.
事实上,上述Cauchy积分公式对逐块光滑边界情形也成立.
2 Sokhotski-Plemelj公式
设区域D及其边界∂D如上所定义.本节中我们讨论Cauchy型积分在边界的极限行为.只对式(1)型Cauchy积分进行研究,式(2)型Cauchy积分与此类似.
定义1当t∈∂D时,积分
(3)
是∂D上的奇异积分.记Ω=∂D-∂D∩St(ε),St(ε)={x∈O‖x-t|<ε}.若极限
存在,则称此极限为奇异积分(3)的Cauchy主值.记
t)(dσ(x)f(x)).
由高斯积分与文献[9],在边界∂D上点t可定义立体角系数α(t)[8].
定义2区域D定义如上,对t∈∂D时,立体角系数为
证明记n(x)为曲面上点x处的外法单位向量,由定理1可知
证毕.
定义3称f(x)∈H(α,∂D),0<α≤1,若对t1,t1∈∂D,有
|f(t1)-f(t2)|≤M|t1-t2|α,
此处,M为一正常数.
定理2设f(x)∈H(α,∂D), 0<α≤1,则奇异积分(3)的Cauchy主值存在,且
等式右端的积分是收敛的弱奇性奇异积分.
证明由引理1,只需证明等式右端的积分是当ε→0时收敛的弱奇性奇异积分即可.由
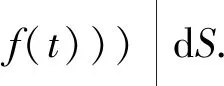
对a,b∈O,容易验证
|ab|=|a|·|b|,
(4)
因而有
上式最后一个积分显然是当ε→0时收敛的弱奇性奇异积分.证毕.
定理3设f(x)∈H(α,∂D),0<α≤1,x、t∈∂D,当|z-t|<δ时,对所有的点z属于以t为顶点的一角形区域内,有
其中δ>0足够小,m为常数,则函数
是∂D上点z=t的连续函数,即当点z由域D的内、外部沿以t为顶点的一角形区域内任何途径趋于点t时,有
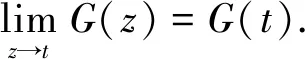
证明首先点z由域D的内、外部沿以t为顶点的一角形区域内任何途径趋于点t时的证明方法是类似的.在此只证明点z由域D的内部途径趋于点t时的极限值.令
σ=∂D∩St(ε),Σ=∂D-σ,
则
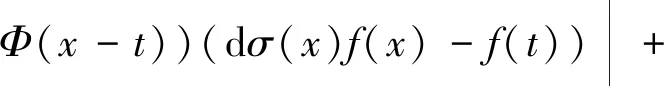
|I1|+|I2|+|I3|,
由Hölder条件和式(4)可得
(5)
式(5)中的最后一个积分显然是当ε→0时收敛的弱奇性奇异积分,于是

我们记F+(t),F-(t)分别是式(3)中F(z)当点z由域D的内、外部沿以t为顶点的一角形区域内任何途径趋于点t时的极限值.由定理2和定理3可以得到如下定理.
定理4(Sokhotski-Plemelj公式)设f(x)∈H(α,∂D), 0<α≤1,t∈∂D,则Cauchy型积分(3)存在内外极限值
(1-α(t))f(t),
且有
F+(t)-F-(t)=f(t),
(dσ(x)f(x))f(t)+(1-2α(t))f(t).

