欧拉数极限值和斯坦纳极值的Python解法

刘洋　王德贵

欧拉数极限值和斯坦纳极值问题，是数学史上著名的数论问题，收录在《100个著名初等数学问题》的第12题和第89题，今天我们用Python来分析和求解。

一、欧拉数极限值问题

1.题目内容

函数

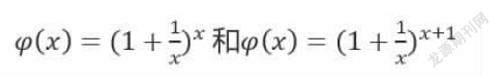
当x无限增大时的极限值。今天我们只求解第一个函数的极限值。

2.算法分析

根据题意，要先判断函数

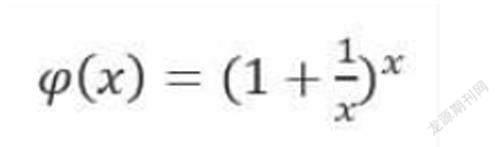
在x无限增大时，是否有极限？如果有极限，是多少？

可以证明，函数在（0，+∞）上是增函数，利用Excel图表处理功能，做出在（0，500）上函数图像如下图，可以看到，在x无限增大时，函数值在2.5-3之间，而且函数值变化很小。

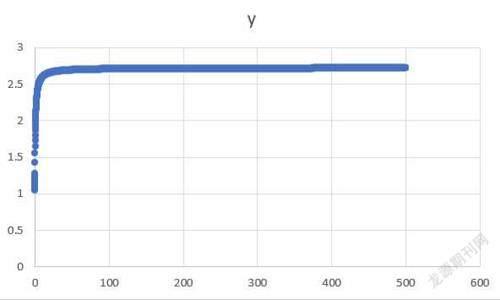
根据题意，我们利用for循环，让x值逐渐增大，来分析y的极限值。

3.程序实现

从前面的分析，写出程序代码。

运行结果如下，大家可以看到，在（1，100）上，y的值逐渐增大，并在2.7左右。

那我们继续增大取值范围，（1，10000）、（1，1000000）、（1，100000000），最后發现，y趋近一个值：2.718281828……

这里用到了数学中的幂函数，在Python里函数pow（x，y）的意义为x^y，也可以表示为x**y，大家使用时注意，用函数pow（x，y）时，需要导入数学模块math，而x**y则不用。

运行结果如下：

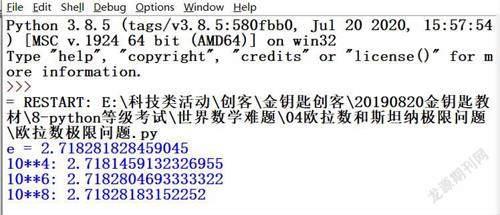
4.结论

我们求解是在10的8次方范围内，10的10次方运行超过了12个小时。从函数值的变化趋势，大家不难发现，这个极限值就是无理数：e。

其实函数

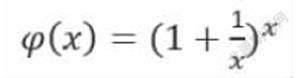
在（0，+∞）上的极限值，也是e的定义。

二、斯坦纳极值问题

1.题目内容

如果x为正变数，x取何值时，x的x次方根为最大？

即求函数

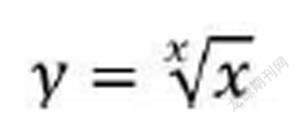
在（0，+∞）上的极值问题。

2.算法分析

这是一个与欧拉极限值相关的函数极值问题，函数在（0，+∞）上，函数值是如何变化的呢？

我们利用Python的for循环，进行分析计算。

下面先测试一定范围内的变化情况，再具体分析。

3.（1，100）上的单调性

运行程序，输出结果如下：

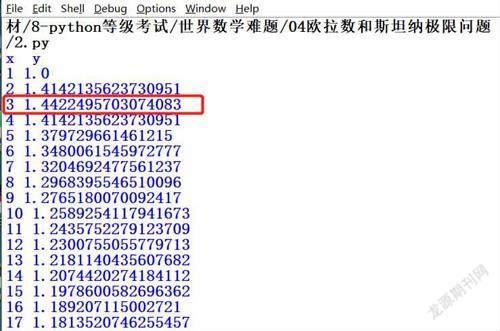
后面的函数值，越来越小了，说明在x=3附近有极值。

4.（2.0，4.0）上的单调性

在x=3附近有极值，那我们就分析在（2.0，4.0）上的单调性，为了保留一位小数，采取除以10的方法。

运行结果如下：

不难发现，函数在x=2.7附近有极值，那么极值点一定在（2.60，2.80）上。

5. （2.60，2.80）上的极大值

进一步分析函数在（2.60，2.80）上的单调性，修改程序，直接求极大值，无须全部输出。

运行结果如下：

6.提高精度，求极大值

我们依次提高精度，求解极大值。

运行结果如下：

7.结论

从以上分析和精度的提高，我们发现，x的值趋近一个特殊值，即x=e时，

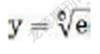
的值最大。

三、认识e

1.常数e

e，作为数学常数，是自然对数函数的底数。有时称它为欧拉数（Euler number），以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数，以纪念苏格兰数学家约翰·纳皮尔（JohnNapier）引进对数。它和圆周率π一样，都是无理数，是数学中最重要的常数之一。

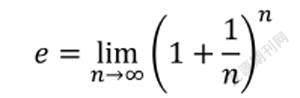
2.关于e的一个问题

将一个数分成若干等份，要使各等份乘积最大，怎么分？

答案是：使等分的各份尽可能接近e值。例如，把10分成10÷e≈3.7份，但3.7份不是整数，四舍五入，所以分成4份，每份为10÷4=2.5，这时2.5**4=39.0625乘积最大，如分成3或5份，乘积都小于39。参见运行结果。

運行结果如下，我们发现4等份时乘积最大：

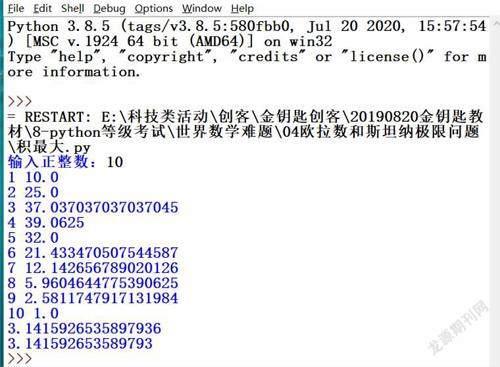
那我们编程直接输出最大项及前后各项，那么为什么除以e呢？

输入整数、小数，是否都可以呢？若是只计算最大值及其前后的两个值，或是只求乘积的最大值，如何编程呢？有兴趣的同学可以去做一下，这里不再赘述。

四、小结

两个问题的结论事先作者也不知道，因而整个求解过程，就是我分析、研究的过程，循序渐进，最后得出结论。也希望这个分析处理问题的思路给学生一个启发：掌握分析方法非常重要。

今天我们认识了e，它是我们数学上很重要的常数。有关e的相关知识，大家可自行查阅相关资料。本文希望大家在学习Python过程中，了解更多的数学史，学习更多的数学知识。