基于半参数广义可加模型的居民个人收入影响因素分析

刁海涛

南京财经大学应用数学学院，江苏南京,210023

在传统统计分析的数据处理中，观测值表示为一组参数的线性函数，而线性回归模型只是观测值与参数关系的近似表达，不能很好地反映实际问题，且模型参数的精度受到测量方法的影响[1]。Engle等引入的半参数回归模型，包含参数部分和非参数部分[2]，与Hastie等提出的广义可加模型结合[3]，产生了半参数广义可加模型，解决了传统线性模型的问题。该模型的参数部分把握因变量的走向趋势，可以外延、适于预测；非参数部分可对因变量进行局部调整，使模型更加精确地拟合样本数据，误判风险降低，避免“维数灾难”[4]。这种模型既含参数分量，又含非参数分量，可以更加灵活地概括和描述更多实际问题，应用更加广泛。本文通过半参数可加模型，分析居民个人收入的影响因素。

1 模型理论基础

1.1 广义可加模型

经典的线性回归模型假定被解释变量Y与解释变量X1,X2,…,Xp是线性形式，如：

E(Y|X1,X2,…,Xp)=β0+β1X1+β2X2+…+βpXp

(1)

其中，β1,β2,…,βp通过最小二乘法获得。

可加模型扩展了线性回归模型：

E(Y|X1,X2,…,Xp)=s0+s1(X1)+s2(X2)+…+sp(Xp)

(2)

其中，si(·),i=1,2,…,p是光滑函数，Esi(Xi)=0，si(·)通过backfitting算法获得。

广义可加模型是线性可加模型的扩展：

g(μ)=s0+s1(X1)+s2(X2)+…+sp(Xp)

(3)

其中，μ=E(Y|X1,X2,…,Xp)，si(·)是非参数光滑函数，它可以是光滑样条函数、核函数或者局部回归光滑函数，它的非参数部分提高了模型的灵活性，揭示出解释变量对被解释变量的非线性影响。

1.2 半参数广义可加模型

若对所有解释变量都进行非参数拟合，则会导致计算量加大和过度拟合等问题。有时可根据实际情况，将被解释变量与部分解释变量的关系简化成参数形式，会更便于解释，即半参数广义可加模型(Semi-parametric Generalized Additive Models)：

(4)

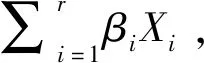
2 数据说明及描述性统计

为研究家庭和受教育环境对居民个人收入的影响，本文选取伍德里奇《计量经济学导论—现代观点》HTV.RAW数据。该数据包含1991年1 230个个人的家庭背景、收入及其他情况，包括wage(每小时收入)、abil(能力，不可观测)、educ(受教育年限)、exper(潜在经验)、urban(是否居住在城市)和lwage(收入的自然对数)等变量，相对全面地呈现了个人成长环境。为方便分析，选择abil、educ、exper、urban、fatheduc(父亲受教育年限)和motheduc(母亲受教育年限)6个变量作为自变量，取lwage为因变量，研究收入的影响因素。分别做abil、educ、exper、fatheduc和motheduc与lwage的散点图(图1和图2)。

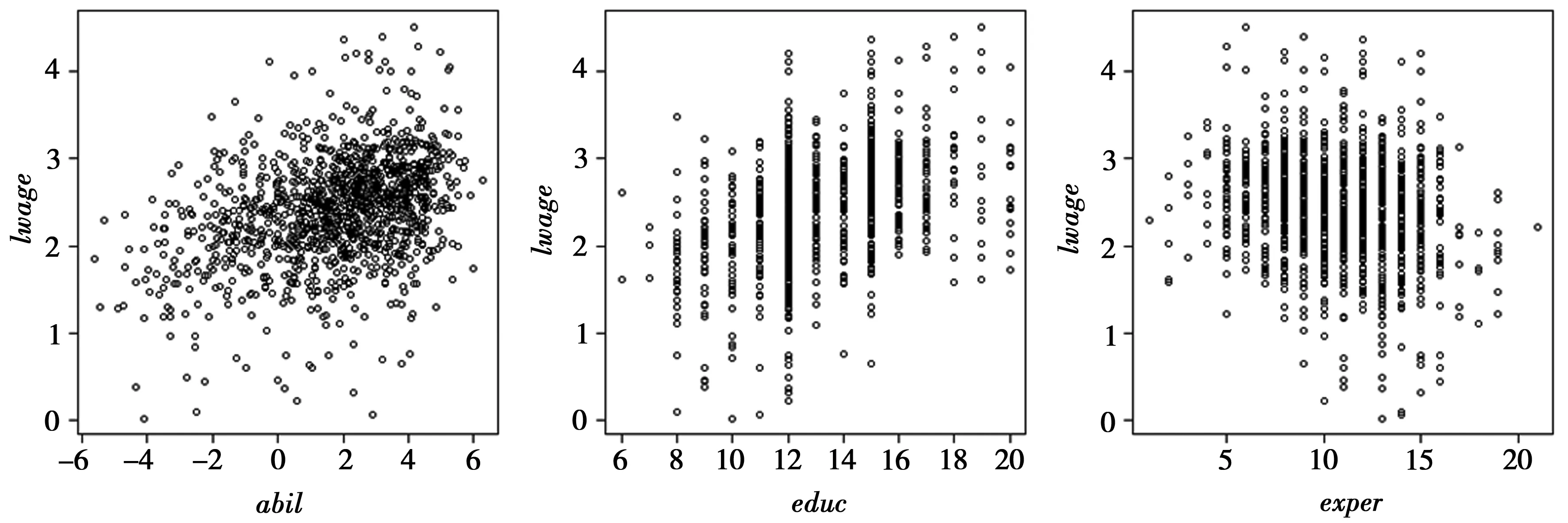
图1 abil、educ和exper与因变量lwage的散点图

图2 fatheduc和motheduc与因变量lwage的散点图

由图1、图2可得：abil与lwage可能存在线性关系，可作为模型的参数部分，exper、educ、fatheduc和motheduc可作为模型的非参数部分的变量。

urban是0～1变量，也作为模型的参数部分。1 230人中有1 005人居住在城市。

3 模型求解

3.1 参数模型

首先，对lwage及其影响因素建立模型Ⅰ—多元线性参数模型，表达式如下：

lwage～exper+urban+educ+abil+fatheduc+motheduc

(5)

根据最小二乘估计思想，利用R软件[5]对模型Ⅰ(式5)进行求解(结果见表1)。

在显著性水平α=0.05下，父母受教育年限的回归系数不显著，说明其对个人收入对数的影响可能是非线性的，其他变量的回归系数均显著，且与收入对数成正相关。

表1 参数模型回归系数估计及检验

注：**表示极为显著，*表示显著。

3.2 半参数广义可加模型

由模型Ⅰ的结果可得，abil、educ、exper和urban对lwage的影响是线性的，作为线性项。而fatheduc和motheduc对lwage的线性影响不显著，作为非参数项，建立模型Ⅱ—半参数广义可加模型，表达式如下：

lwage～abil+exper+educ+s(fatheduc)+s(motheduc)+urban

(6)

用R软件对模型Ⅱ式(6)参数项和非参数项进行估计[6]，结果分别见表2和表3。

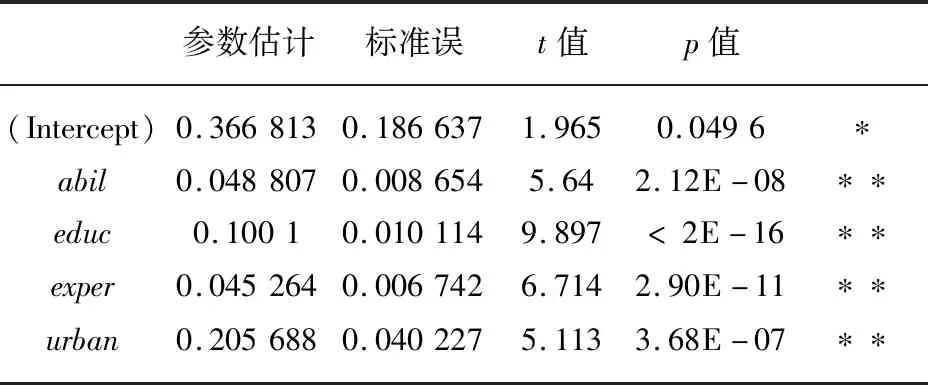
表2 模型Ⅱ参数部分估计结果

注：**表示极为显著，*表示显著。

由表3可得，在显著性水平α=0.05下，截距项和参数项都是显著的，说明模型参数部分拟合效果较好。截距和四个参数的系数都是正值，其中，educ与urban对lwage的影响相对较大，而abil和exper的影响相对较弱。

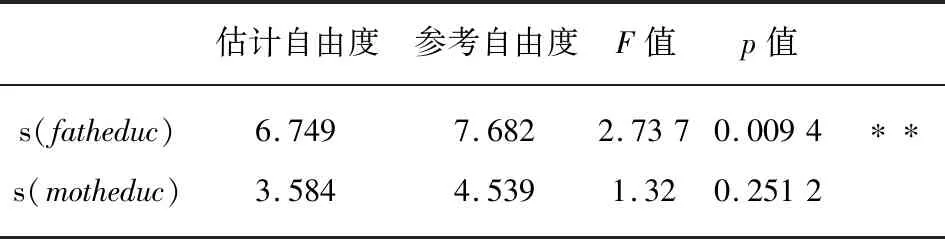
表3 模型Ⅱ非参数部分估计结果

注：**表示极为显著。

对比表3和表1，父母的受教育年限对个人收入对数的非参数效应大于参数效应，对应的p值表示平滑函数是否显著地减少了模型误差。fatheduc的影响强于motheduc的影响，motheduc的非参数效应不是很显著。fatheduc对lwage的非线性影响具体见图3。

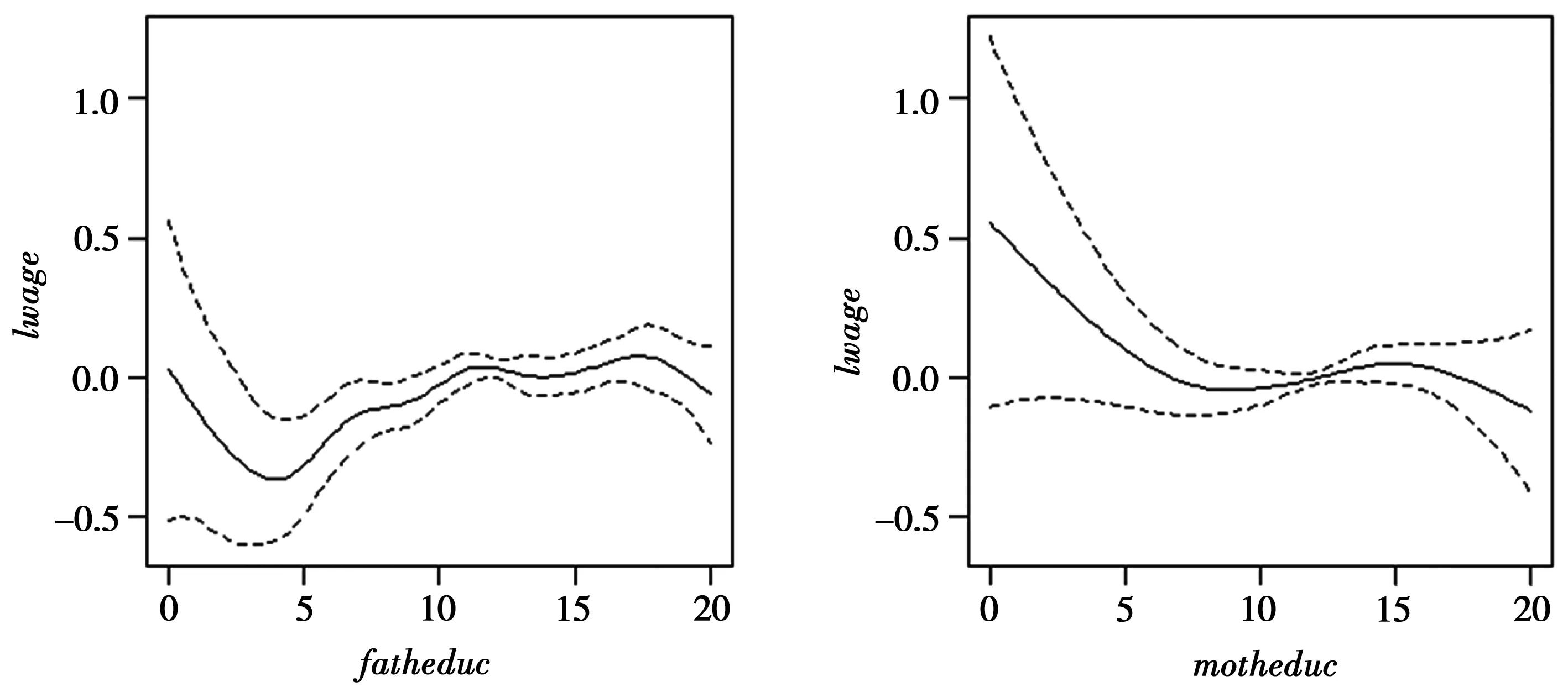
图3 半参数广义可加模型中父母受教育年限因素的非参数效应

图3表明，在该半参数广义可加模型中，fatheduc对lwage的影响不是单增或单减。当fatheduc较低时，lwage随着fatheduc的增大而减小；当fatheduc大于5且小于18时，lwage随着fatheduc的增大缓慢增长，当fatheduc大于18时，lwage有减小趋势。而motheduc对lwage的影响相对较单一，影响整体呈负向。当motheduc低于8时，lwage随着motheduc的增大而快速减小；当motheduc在8到15之间时，lwage有很缓慢的增长趋势；当motheduc大于15后，lwage又出现下降趋势。

4 结 语

本文将半参数回归与广义可加模型结合，并应用到居民个人收入的研究中。结果表明，在影响个人收入的诸因素中，个人能力、受教育年限、潜在经验、居住在城市对居民个人收入的影响是参数效应，且均为正向效应。其中受教育年限和城乡因素对收入的影响相对较大，而个人能力和潜在经验影响相对较小。而父母受教育年限对收入影响是非参数效应，不同教育年限对收入影响趋势不同。父母受教育年限小于5年，对收入影响均呈现不同程度的负效应；当受教育年限为10～15年时，父亲受教育年限对收入的正向影响大于母亲。