多尺度视角下装备维修经费序列波动特征与事件影响分析

蒋铁军， 张怀强， 周成杰

(海军工程大学管理工程与装备经济系，湖北 武汉 430033)

装备维修保障工作受到各种内在和外在因素的影响，这些影响的显性表现形式多种多样，反映到经济层面主要是装备的维修经费，且在不同时期这些因素的影响具体体现为维修经费序列的波动。装备维修经费序列通常呈现出显著的非线性、非平稳性和多尺度等特性，尤其是各类事件的影响，如：等级修理、各类演习训练任务、现代化改装，以及经济环境的剧烈波动等，往往还会使经费序列产生结构突变，使传统经费预测和决策模型的适应性显著变差，分析难度加大[1]。随着装备执行多样化军事任务的频率和强度不断增加，以及经济环境的动态变化，各类事件对装备维修经费的影响将愈加显著。

通过分析装备维修经费序列随时间推进的波动特征，有效地识别经费序列的结构性变化，能够在一定程度上了解各种因素的影响变化以及事件的影响情况，为开展相关预测和决策分析提供基础支撑。

装备维修经费序列是一类典型的经济时间序列。传统的时间序列波动特征和事件影响分析方法通常直接针对序列本身展开，由于时间序列影响因素及其构成的复杂性，效果往往不是太好。随着多尺度分析方法的不断提出，从多尺度视角辨识时间序列的有效构成，在不同尺度上分析分量序列的发展变化规律是目前采用较多的一种处理办法[2]。对时间序列进行多尺度分析，关键是要对序列进行有效的多尺度分解。传统的序列分解方法主要有傅立叶谱分析、小波分析等[3-4]，这些方法的优势在于可以很好地处理非平稳、非线性信号，且直观、简单，但也存在一定的不足，如：傅立叶谱分析在时域内不具有分辨率，小波变换不能实现自适应多分辨率分析等[5]。ZHU等[6]提出的经验模态分解(Empirical Mode Decomposition，EMD)算法可以基于原始时间序列的局部特征，直接提取出一种固有模态函数(Intrinsic Mode Function，IMF)，进而实现序列的自适应分解。相对于传统分解方法，其具有更强的原始特征和局部特性识别能力，是目前开展时间序列多尺度分析的较好方法之一[7]。

在事件对时间序列的影响分析方面，通常采用检验方法识别序列中的结构变点，如：Chow检验[8]、Quandt-Chow检验[9]、BP检验[10]、CUSUM-SQ检验[11]等。其中，INCLAN等[12]基于中心化累积平方和方法，改进性提出了迭代累积平方和(Iterative Cumulative Sums of Squares，ICSS)算法，用于寻找序列在不同时点的突变点，该算法能实现序列中多个结构性方差变点的识别，且简便易行、效果较好，已被广泛应用于解决各类时间序列的变点识别问题[13-14]。

鉴于EMD算法在序列分解上的优异性能以及ICSS算法在序列结构变点检验中的良好表现，笔者集成二者的优势，提出了多尺度视角下的装备维修经费序列波动特征与事件影响分析方法。首先采用EMD算法对原始经费序列进行多尺度分解，获取其基本构成、波动特征和各类因素的影响情况，然后针对每个分量，分别采用ICSS算法进行结构变点识别，从深层次揭示装备维修经费序列的波动特性，以及事件对经费序列内在结构变化的影响。

1 经费序列分量波动特征分析指标选取

由于装备维修经费的不同IMF的发展变化趋势可能存在较大差异，笔者主要通过统计分析方法对不同IMF进行波动特征分析。采用的统计指标主要有IMF的平均周期(平均周期)、IMF的方差及其相对于原始经费序列的方差占比(方差贡献率)、IMF与原始经费序列的Pearson系数和Kendall系数[14]。各项指标的具体含义如下：

1) 平均周期。周期是时间序列波动的典型特征之一。由于原始经费序列经EMD算法分解后，各IMF的频率往往会随时间变化，因此，应采用平均周期描述各IMF的频率变化情况，即

T=2L/s。

(1)

式中：T为IMF的平均周期；L为IMF的长度；s为波峰和波谷的数量。

2) 方差贡献率。EMD分解的目的之一是分析不同尺度分量对总体经费序列变化的影响。由于各IMF彼此基本相互独立，因此，可以利用方差占比描述各IMF对原始经费序列的贡献度，即

(2)

3) 相关系数。相关系数用于衡量各IMF与原始经费序列之间的相关性。Pearson系数和Kendall系数主要用于衡量数量相关和等级相关[15-16]，其中

Pearson系数的计算公式为

(3)

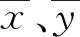
Kendall系数的计算公式为

(4)

式中：ωij=(xj-xi)(yj-yi)。

对于任意给定的数据对(xi,xj)和(yi,yj)，若(xj-xi)(yj-yi)>0，则二者等级一致;否则,不一致。

2 经验模态分解

EMD认为时间序列是由不同尺度上的基本分量(IMF)构成，通过分解可以实现序列的平稳化，同时可将序列原本的构成特征展示出来。

该算法的基本实现步骤如下[15]：

1) 对任一给定时间序列s(t)，确定其所有极值点；

2) 根据极值点用三次样条曲线作上下包络线；

3) 计算包络线均值m11(t)，得到该序列与均值之差h11(t)=s(t)-m11(t)；

4) 将h11(t)视为s(t)，重复步骤1)-3)，若h1(k-1)与h1k的方差小于某值，则h1k为1个IMF，此时c1=h1k，r1(t)=s(t)-c1；

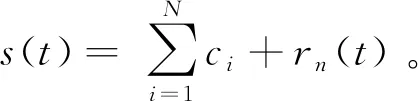
3 迭代累积平方和

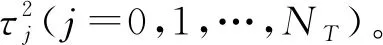
Dk=Ck/CT-k/T，

(5)

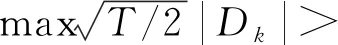
4 经费序列波动特征与事件影响分析框架

多尺度视角下的装备维修经费序列波动特征与事件影响分析框架如图1所示。

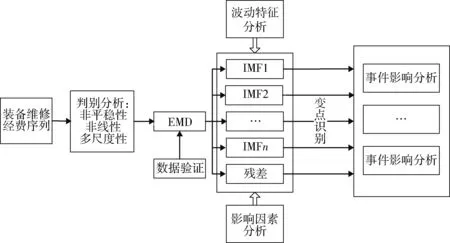
图1 装备维修经费序列波动特征与事件影响分析框架

具体分析步骤如下：

1) 原始经费序列判别分析。将统计检验和经验分析相结合判别原始经费序列的基本特性。

2) 原始经费序列多尺度分解。运用EMD算法对原始经费序列进行分解，从多个层面更加细致地研究原始经费序列的发展变化规律。

3) 经费序列分量波动特征及影响因素分析。计算不同IMF的统计指标，分析经费序列的波动特征以及不同因素对不同IMF的影响。

4) 经费序列分量变点识别。通过对变点统计检验和现实事件影响的对比分析，确定经费序列结构发生重大变化的时间点。

5) 事件影响分析。比较分析变点前后经费序列分量统计特征的变化，判别事件对经费序列的影响，结合背景知识，分析事件类型及其对经费序列的影响机理。

5 应用分析

5.1 数据获取

舰船维修器材经费由于受器材故障规律、装备使用强度、管理模式，以及各种事件(如临时检修、人员误操作、等级修理、现代化改装)等多重因素的影响，其序列表现出较强的非线性、非平稳和多尺度等特性[16]。

因此，笔者以某型舰船装备维修器材经费数据为对象开展应用分析。

5.2 原始经费序列判别分析

采用ADF(Augmented Dickey-Fuller)方法判别原始经费序列的非平稳性，计算得到在显著性水平1%、5%和10%下的临界值分别为-2.590 7、-1.944 4和-1.614 1，序列的统计量为1.302 7，P值为0.950 5，表明原始经费序列具有非平稳性，该序列可能包含趋势、季节性或周期性等成分，这一特征比较符合装备故障的一般规律以及计划筹措与临时筹措相结合的常规做法。

采用BDS(Brock,Dechert & Scheinkman)方法判别原始经费序列的非线性[17]，计算标准差分别为0.5、0.75、1、1.25和1.5，嵌入维数从2到10的BDS统计值，具体如表1所示。从表1可以看出：BDS统计值均大于显著性水平为5%时的临界值(1.96)，表明原始经费序列具有非线性，这一特征也进一步验证了经费受到多重因素的影响，且相互之间存在着较为复杂的非线性关系。

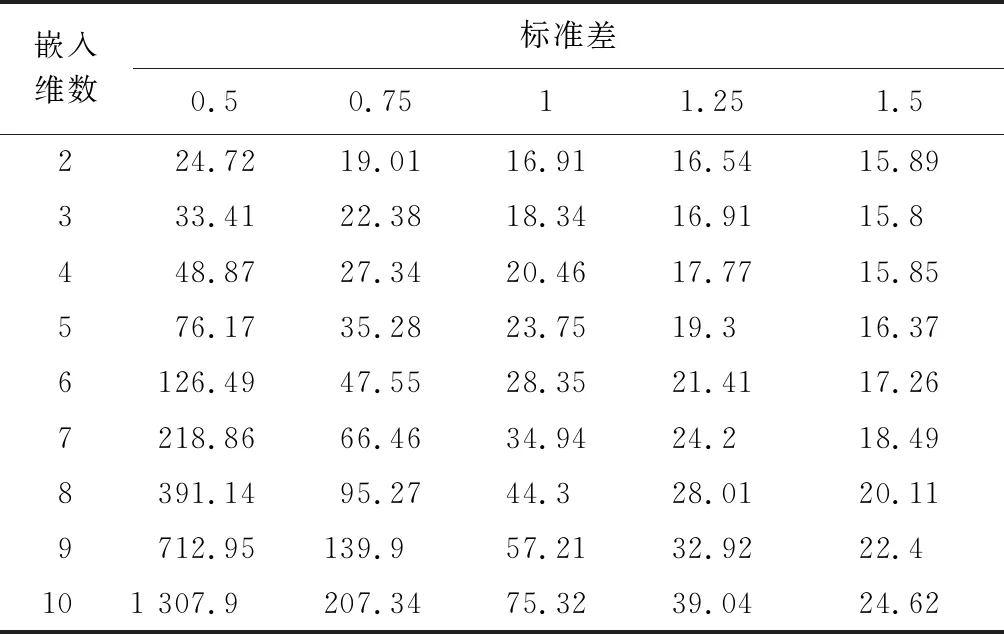
表1 原始经费序列的BDS统计值

对于原始经费序列的多尺度性，根据器材经费受随机性故障、装备使用强度、管理模式以及各种事件对经费序列产生影响程度的不同，可初步判定经费序列具有多尺度性。该特性也将结合序列分解进一步得到验证。

5.3 时间序列分解

EMD算法对原始经费序列分解的具体情况如图2所示。从图2可以看出：1)原始经费序列被分解成了4个IMF，不同IMF具有不同的频率水平；2)IMF的振幅和频率负相关，即频率越高，振幅越小；3)IMF4(残差序列)去除了高频波动，基本维持了原始经费序列的趋势水平；4)原始经费序列具有明显的多尺度性，通过序列分解，能够更加细致地观察经费序列的发展变化规律。

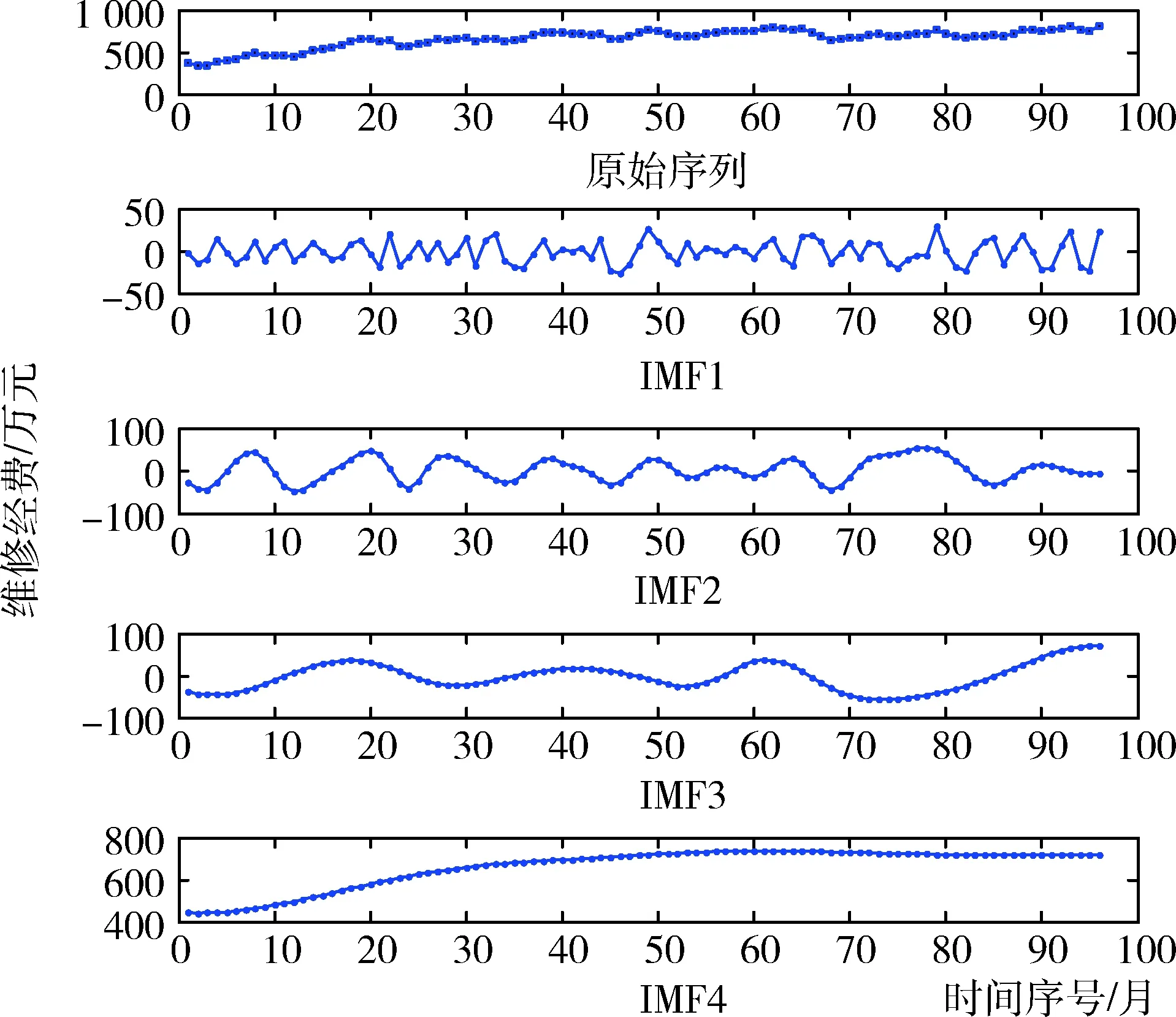
图2 基于EMD算法的原始经费序列分解

5.4 经费序列分量波动特征与影响因素分析

5.4.1 经费序列分量波动特征分析

通过对不同IMF和原始经费序列的统计计算，可以得到如表2所示的相关统计指标值。

从平均周期看，IMF1、IMF2的平均周期分别为3.6月和10.1月，均在1 a以内，相对较短，是典型的高频序列，其振幅集中在55以内；IMF3的平均周期较IMF2、IMF1有所加长，约2 a左右，属低频序列，振幅也略有增加；残差序列无明显周期性，大约自第10月开始，呈先快速上升后逐渐趋于平缓的态势，与原始经费序列的发展趋势大体一致。表明经费的周期性变化主要受到装备战训任务、等级修理周期等因素的影响，但长期发展趋势仍以装备故障规律的影响为主。

表2 不同IMF的统计指标值

从方差贡献率看，残差分量对原始经费序列走势影响最明显，达到82.16%。各IMF的贡献率随频率水平的增加而减小，如IMF1的贡献率仅为1.68%。

从相关系数看，基本规律与方差贡献率类似。残差分量与原始经费序列的相关程度最为显著，Pearson、Kendall系数分别为0.928 5和0.580 1。其他IMF随着频率水平的增加，其相关程度逐步降低。表明经费的总体变化主要受到装备故障规律等低频分量的影响，随机性、突发性故障等高频分量的影响会随着频率增加而逐渐减弱。

5.4.2 经费序列分量的影响因素及其影响机理

通过上述统计分析，可以大致看出不同IMF的基本变化规律及其与原始经费序列的相互关系，这些规律是各种因素综合影响的具体体现。

1) 高频分量(IMF1、IMF2)。高频分量的波动幅度不大、频率高、规律性差，对经费序列的长期趋势影响不大，如制订维修器材中长期筹措规划时，往往可以忽略这一影响；但短期影响则较为显著，是制订季度或月度器材筹措计划需重点考虑的内容。

根据舰船装备管理工作的具体实际，维修器材经费在短期内主要受到装备随机故障及不确定事件的影响。在舰船的日常使用中，往往存在着一些不可预知的事件，如：各类设备的随机性、突发性故障，人员操作存在偶然的失误等，这些都使得维修器材需求在短期内发生变化，且具有一定的随机性和跳跃性。这些事件的特点是发生较为频繁、持续时间相对较短，其对经费序列的影响主要体现在IMF1、IMF2这样的高频分量中。

2) 低频分量(IMF3)。低频分量的变化介于趋势分量和高频分量之间。低频分量与原始经费序列的形态具有一定的一致性，尤其是在序列发生剧烈变化的时间点，往往对应着重要的事件。在低频分量中，序列受事件影响后，其变化趋势会产生较大波动，虽然短期内有一定缓和，但还是会持续较长时间。IMF3的平均周期约为2 a，说明了在没有其他重要因素干预的情况下，分量序列在短期内难以自行消除事件的影响。

此外，低频分量在很多时点的振幅都在原始经费序列的8%左右，平均变化量占原始经费序列的比例为4%，说明事件对原始经费序列的影响程度也是比较大的。从目前的舰船维修保障现状来看，主要原因在于事件对装备维修保障系统造成了重要影响，使维修保障系统的内外部环境发生了重要变化，进而对经费变化规律产生了重要影响。

3) 趋势分量(IMF4)。趋势分量表现了原始经费序列的长期走势，与其具有很强的相关性，可以为今后经费预测提供基本参考。从原始经费序列的发展趋势可以看到：虽然在某个时间点会由于某些因素的影响产生波动，但当影响消退后，还是会回归到基本趋势。趋势分量体现了原始经费序列的基本走向，体现出经费受到内、外多种因素综合作用的结果，表现为相对固有的发展规律。

趋势项总体呈上升态势，这与舰船维修保障的基本规律是一致的。随着舰船入役时间的不断延长，系统设备的老化不断加剧、故障率不断增加，维修器材的价格也在不断攀升，这些内在、外在因素基本决定了维修器材经费的上升趋势。虽然期间可能会对部分系统设备进行更新换代，其故障率在短期内有所缓和，维修经费会出现下降，但是经过一段时间之后，基本的上升趋势同样会继续保持下去。

需要注意的是，某些重大事件可能对经费序列的趋势项产生根本的结构性影响，如：大规模的改换装工程，由于装备配置的根本性改变，系统设备的故障规律会发生本质变化；维修经费的构成内容重新进行了调整，维修经费计算执行了新的规范，维修经费的统计计算结果也将会发生实质性变化。

5.5 经费序列分量的变点检验

采用ICSS算法分别对原始经费序列和各分量序列进行变点检验，结果如表3所示。

由表3可以看出：1)原始经费序列、IMF1、IMF2均无变点，即事件未对这些序列的结构趋势产生影响；2)IMF3的结构在第22月和69月发生突变，变点前后序列的趋势发生了较大变化，但是原始经费序列转折点与变点并不完全一致，主要是因为事件影响往往是在相对较短的时期内不断显现出来，如图3所示；3)IMF4也无变点，与原始序列一致，表明事件还未强烈到影响经费序列的基本趋势；4)原始经费序列无变点，但IMF3有变点，进一步表明从多尺度视角研究装备维修经费序列波动特征和事件影响的必要性。

表3 ICSS算法变点检验结果(置信度95%)

5.6 事件对经费序列分量的影响分析

采用对变点前后序列进行统计的方法，分析事件对IMF3产生的影响。

5.6.1 变点1的影响分析

第1个变点前后数据序列的统计结果如表4所示，可以看出：分量序列的方差变小、振幅均值变小，说明经过事件后，序列的波动幅度呈现相对平缓的趋势。主要原因是装备经过局部改装，部分设备换代升级，故障规律相应发生变化，且故障率降低。但由于改装初期的磨合问题，故障率会短期内小幅波动，随后一段时间内总体降低且呈现平稳态势。

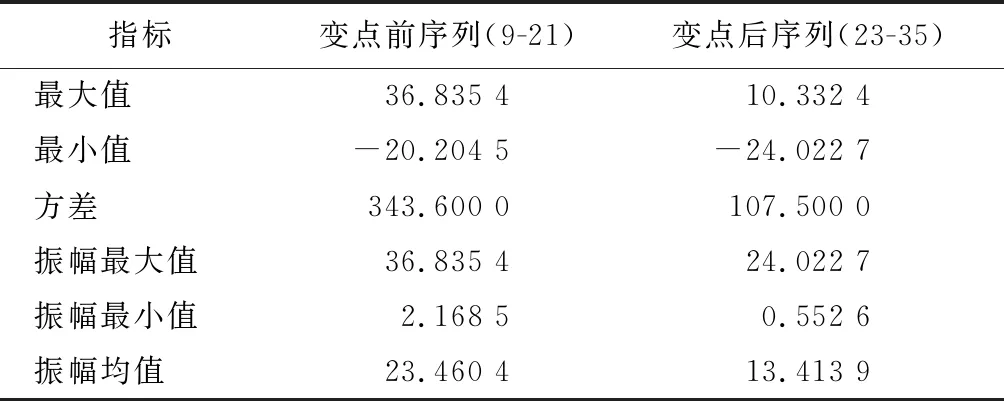
表4 变点1前后数据序列的统计情况

5.6.2 变点2的影响分析

第2个变点前后数据序列的统计结果如表5所示，可以看出：分量序列的最大值变大、最小值变小、方差变大、振幅均值变大，说明经过事件后，分量序列的波动在不断增大。主要是因为装备使用强度增加使故障率增大。但事件发生后短期内，器材消耗有所降低，主要是在事件点开展了等级修理，装备技术状态得到一定程度的恢复，但随着使用强度的持续加大，序列随后出现大幅波动。

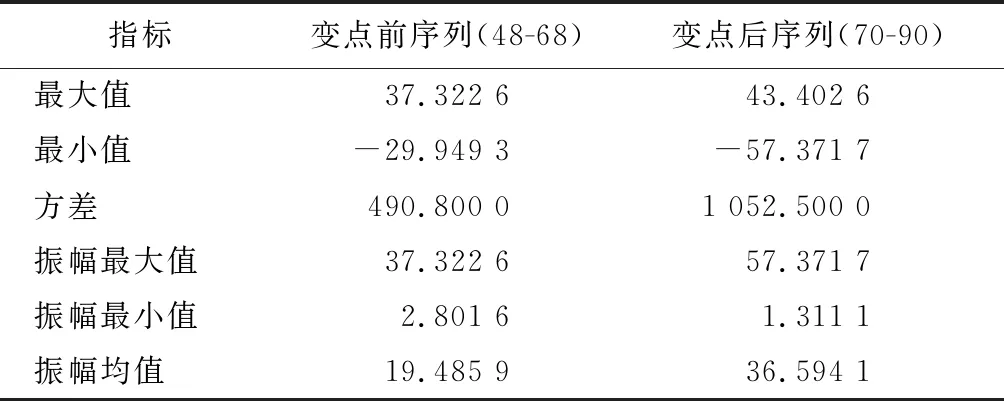
表5 变点2前后数据序列的统计情况

6 结论

笔者主要针对装备维修经费序列表现出的非线性、非平稳性、多尺度等特性，运用EMD算法对其进行分解，进而从多尺度视角对经费序列开展波动特征和事件影响分析。结果表明：

1) 装备维修经费序列主要受到自身发展趋势、各类事件和随机故障等多重因素的影响，具体体现在分解后的不同尺度序列上；

2) 不同因素对原始经费序列的影响效果不尽相同，自身发展趋势体现了经费序列的基本内在规律，事件影响着经费序列在较长一段时期的剧烈波动，而随机故障则使经费序列产生不规则的短期波动；

3) 针对EMD算法分解后的经费序列分量开展变点检验，相对于直接针对原始经费序列的检验更加有效，表现出更强的辨识能力；

4) 识别出的经费序列分量变点，与现实情况基本一致，进一步验证了方法的有效性和可靠性；

5) 通过对变点前后数据序列变化情况的统计分析，基本符合对现实事件分析得出的一般规律。