基于特殊任务Prophet模型的航材消耗需求预测模型

周家萱， 徐常凯

(空军勤务学院航材四站系， 江苏 徐州 221000)

航材根据其订货属性可分为有寿件、可修件和消耗件3大类[1]。其中有寿件和可修件具有明确的寿命控制时次和平均故障间隔时间，可依据其消耗机理建立消耗需求预测模型；而消耗件由于其消耗量的随机性大，难以依据其消耗机理建模。因此，消耗件需求预测是航材需求预测的重点和难点问题[2]。

时间序列分析[3]是根据系统观测到的时间序列数据，通过曲线拟合和参数估计建立数学模型的理论和方法。当前，普遍采用时间序列分析方法进行航材消耗需求预测。由于在航材消耗历史数据中，存在大量的重复模式、数据拐点、离群点以及由于常态性特殊任务(如部分法定假日的常态性任务、演习训练等)造成的突发性航材消耗数据(特殊点)，应用传统的时序预测模型(如ARMA等)进行预测时，通常是将这些特殊点划分为离群点而剔除[4-5]，从而完全忽略了这些特殊点对预测模型估算精度的影响，但在工作实践中，这些特殊点对于航材保障需求预测工作具有十分重要的意义。Prophet模型能够将特殊任务造成的异常消耗数据纳入时序预测建模过程，进而解决了航材消耗需求时间序列预测问题。笔者首先分析了特殊任务航材消耗需求预测的特点和要求，应用考虑特殊任务因素的Prophet时序预测模型对航材消耗过程进行建模，利用Prophet模型来解决航材消耗时间序列预测问题，并与无特殊任务Prophet模型和传统时序预测模型进行了对比，最后通过实例验证了Prophet模型的有效性。

1 特殊任务航材消耗需求预测特点与要求

随着军队新大纲施训的全面展开，航空兵出动规律逐渐从以飞行小时为牵引转向以飞行任务为牵引，出现了大型演习和实战化飞行训练等常态化任务飞行时间。相比于以飞行小时为牵引的飞行科目，有飞行任务的训练科目其实战化程度更高、强度更大。特别是对于飞机发动机而言，实战化科目造成其加力时间延长，热循环次数显著增多，由此产生大量突发性的、高消耗的航材消耗数据。表1为飞机发动机减震垫的日常消耗和特殊任务消耗的部分数据。

表1 飞机发动机减震垫消耗部分数据 件

由表1可以看出：该航材在日常使用状态下的消耗量较少，而在特殊任务情况下其消耗量呈数十倍的增长。当应用传统的时序预测模型进行消耗需求预测时，该类数据通常被识别为离群点而被剔除，导致预测误差较大。

2 Prophet模型的预测原理

Prophet模型采用时间序列分解分析方法，以时间t为自变量，利用时间序列数据对趋势项、季节项、特殊任务项和误差项4项参数进行拟合[6]，即

y(t)=g(t)+s(t)+h(t)+ε。

(1)

式中：g(t)为趋势项，表示时间序列中非周期性的变化趋势；s(t)为季节项，表示时间序列中周期性的变化趋势；h(t)为特殊任务项，表示在采集数据时间段内是否有特殊任务；ε为误差项。

2.1 趋势项g(t)

Prophet模型利用逻辑回归函数和分段线性函数拟合趋势项。其中：逻辑回归函数的一般形式为[7]

(2)

式中：C为曲线的最大渐进值；k为曲线的增长率(基础增长率);m为曲线的中点。在实际需求预测建模中，这3个参数都不是常数，均随时间t的变化而变化，即C=C(t),k=k(t),m=m(t)。

时间序列曲线的变化往往是通过一定数量的变点，使曲线呈周期性变化趋势，设sj为第j(j=1,2,…,S,)个变点对应的时刻，δj为变点在sj时刻的增长率，服从拉普拉斯分布，即δj～Laplace(0,τ)，用来调节变点增长率的变化情况，其中τ为拐点影响力，τ越大，允许模型适应的波动强度越大。定义指示变量

(3)

则在任意时刻t的变点增长率为k+αTδ，其中δ=(δj,j=1,2,…,S),为变点增长率向量;α=(αj(t),j=1,2,…,S),为指示向量。由于拐点会导致函数非连续，因此需要在拐点处进行平滑处理，增加偏移量。根据拉普拉斯变换对拟合曲线进行平滑处理，可得在变点sj处的平滑处理偏移量γj为[8]

(4)

任意时刻t的偏移量为m+αTγ，γ=(γj,j=1,2,…S),为变点的偏移向量，则逻辑回归函数拟合的趋势项为

(5)

分段线性函数在每一段的表达式为y=kx+b，由逻辑回归函数的参数值可得分段线性函数为

g(t)=(k+αTδ)×t+(m+αT(-Sδ))。

(6)

2.2 季节项S(t)

Prophet模型通过建立周期序列的傅立叶级数的周期性变化趋势来拟合季节项，即

(7)

式中：P为目标序列可预计的常规周期，如周、年、月等，拟合的关键是首先确定N(N为季节影响力)的最优值，然后再拟合β=(a1，b1；a2，b2；…；aN,bN)T，其中β为对季节项模型进行平滑的参数，服从β～N(0,σ)的正态分布，σ越大，允许模型的波动性越强。

根据傅立叶级数的原理，缩短N的序列可理解为低通滤波器，因此，设置大N值可适应强季节变化，但容易造成过拟合。参考文献[9]的研究结果：以年为周期的序列，N最优值=10，以周为周期的序列，N最优值=3，因此式(7)可调整为

(8)

2.3 特殊任务项h(t)

Prophet模型假设不同的特殊任务之间是相互独立的，即不同任务分别代表不同的模型。设L为周期内特殊任务的数量，Di为第i项特殊任务对应的时间列表，1{t∈Di}表示时间t是否在任务期间内，则

(9)

另外，特殊任务会影响任务前后一段时间的时间序列，分别称其为任务的前置窗口和后置窗口，因此需要将单一日期t转换为关于特殊任务日期和时间窗口的特征矩阵Z(t)，并将模型的数学表达式调整为与式(7)一致的处理形式，即

h(t)=Z(t)k。

(10)

式中：Z(t)=(1{t∈D1},…,1{t∈DL})；k=(k1,…,kL)T,k～N(0,v2)；v为任务影响力，表示特殊任务项对拟合的影响程度，v越大，允许模型适应的波动越大。最后，利用极大后验概率或Markov Chain Monte Carlo(MCMC)算法对参数β和k进行估计。

3 实例分析

3.1 数据拟合与预测

以飞机发动机减震垫(册序号：发动机减震垫；型号：Y8-6400-8)为例，验证模型的合理性。该航材从2012-01-01至2018-12-31共7年的历史消耗数据散点图如图1所示。

图1 飞机发动机减震垫7年的消耗数据散点图

由图1可以看出：飞机发动机减震垫的历年消耗数维持在0～50件，消耗量较为稳定，但在2012、2014、2015、2016、2017、2018年消耗量都有突变，特别是在2014-2015年期间消耗量有近10次的突变，在排除数据记录问题后，确定这些数据突变点与特殊任务的时间点一致。特殊任务时间点及飞机发动机减震垫的消耗数如表2所示。

表2 特殊任务时间点及飞机发动机减震垫消耗数件

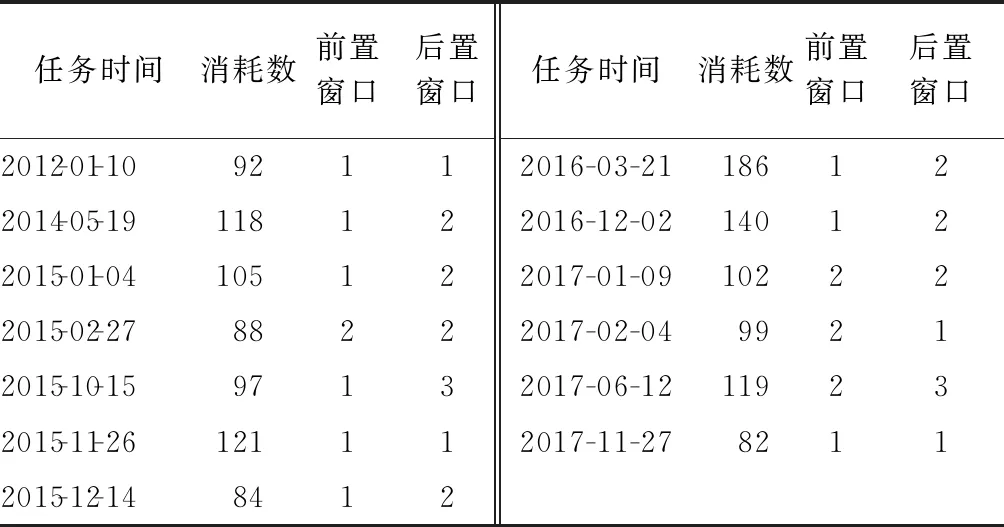
任务时间消耗数前置窗口后置窗口任务时间消耗数前置窗口后置窗口2012-01-1092112016-03-21186122014-05-19118122016-12-02140122015-01-04105122017-01-09102222015-02-2788222017-02-0499212015-10-1597132017-06-12119232015-11-26121112017-11-2782112015-12-148412

由于飞机航材质控系统所收集的消耗数据皆为流水数据，通常采取滚动计算方法预测下一年的消耗量，即使用前N年的消耗数据预测第N+1年的消耗量。笔者将消耗数据分为训练数据和测试数据2类，其中：2012-01-01至2017-12-31的消耗数据为训练数据，2018-01-01至2018-12-31的消耗数据为测试数据，并以“天”为粒度整理成连续时间序列，最后，利用线性模型拟合数据。参考文献[10]中的参数设置，结合航材实际消耗情况确定Prophet模型的拟合参数如表3所示。

以特殊任务点2015-12-14(前置1窗口，后置2窗口)的消耗数据为例，利用Prophet模型对2015-12-12至2015-12-17共6天的趋势项g(t)、任务项h(t)、预测项y(t)的拟合结果如表4所示。

表3 Prophet模型的拟合参数

由表4可以看出：在特殊任务点2015-12-14的当天、前1天和后2天，任务项拟合值均不为0，即特殊任务数据参与了模型的数据拟合，特别是在任务当天，任务项的拟合值为70.693 2，而预测值为71.616 4，二者与实际消耗值84非常接近。在2015-12-12和2015-12-17，任务项没有拟合值，其预测值与无特殊任务的消耗情况相似。

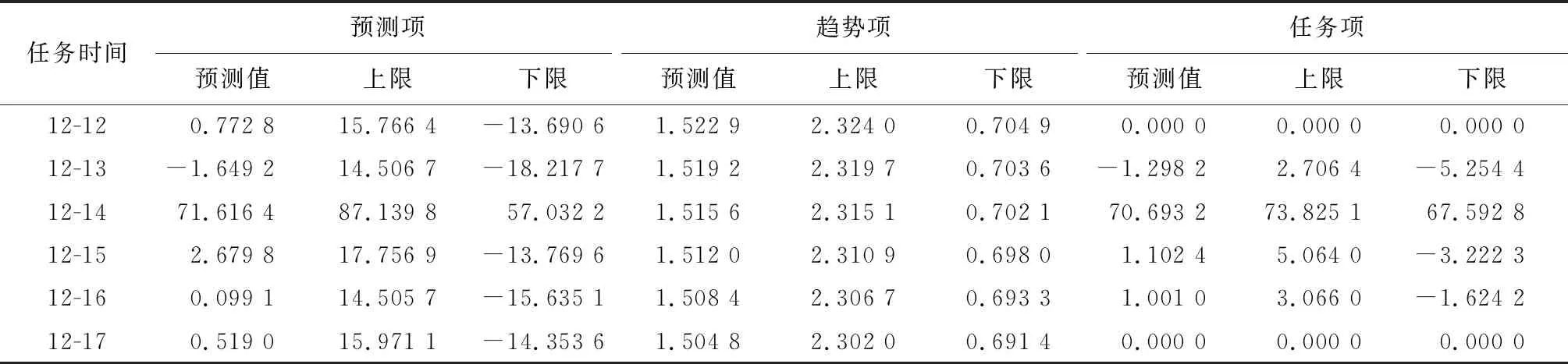
表4 Prophet模型对2015-12-12至2015-12-17的趋势项g(t)、任务项h(t)和预测项y(t)的拟合结果

图2为飞机发动机减震垫消耗量序列按任务、年度、月份、星期的分解情况。

图2 飞机发动机减震垫消耗量的序列分解

1) 由图2(a)可知：该航材在无特殊任务期间的消耗趋势基本平稳，但在特殊任务期间的消耗量接近75件，超过无特殊任务消耗量的70倍。

2) 由图2(b)可知该航材的消耗趋势为：在2012-2014年度较为平稳，日均消耗量为1件，在2014-2016年间出现了1次小幅波动，日均最大消耗量为2.7件，从2016年5月以后，消耗量整体呈上升趋势。

3) 由图2(c)可知：该航材的消耗具有一定的节假日特性，在传统的长假期间(如春节、国庆节)消耗量出现明显下降，但在法定假日没有明显下降，这一规律符合航空兵部队的工作规律。

4) 由图2(d)可知该航材的日常消耗量具有明显的双休日特性：在周末期间的消耗量最小，在工作日内，消耗量最高点出现在前半周，随着时间临近周末，消耗量明显下降。

图3为2012-2018年度消耗数据的拟合结果以及2018-2019年度消耗量的预测结果。

由图3可以看出：Prophet模型有效拟合了特殊任务点的实际消耗量，及其对总体消耗趋势的影响。特殊任务点消耗量拟合分布在(80,100)的区间内，对总体消耗量的影响趋势分布在(70,80)的区间内，这一结果与图2(b)的分析结论是一致的，且呈现出与图2(d)一致的长假期的消耗特性。在预测区间[2018-01-01,2018-12-31]内，共有365个数据点，其中354个点落在95%的置信区间，预测值为1 383，预测上限为2 223，预测下限为602，考虑特殊任务的Prophet模型的预测结果如图4所示。

由此可见：考虑特殊任务的Prophet模型能够有效拟合特殊任务的消耗数据，其时间序列拟合趋势符合航材消耗实际情况，且最终的预测上、下限包含了真实的消耗数据。

图3 Prophet模型对飞机发动机减震垫消耗数据的拟合及预测结果

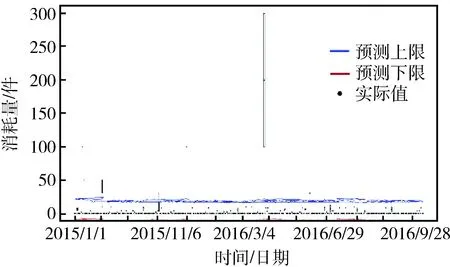
图4 考虑特殊任务的Prophet模型的预测结果

3.2 模型预测结果对比分析

为验证考虑特殊任务的Prophet模型拟合特殊任务数据的精确性和预测结果的合理性。随机生成1年的飞机发动机减震垫的消耗数据，期间存在特殊任务的时间和对应的消耗量如表5所示。

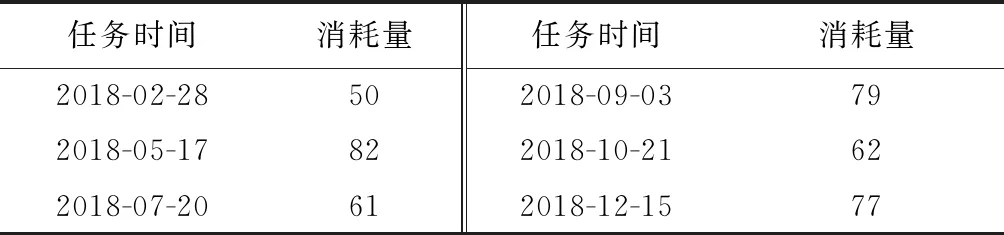
表5 特殊任务时间及其消耗量 件

分别利用考虑特殊任务的Prophet模型、无特殊任务Prophet模型和ARMA模型对表5中的数据进行拟合，拟合曲线如图5-7所示。

由图5-7可以看出：考虑特殊任务的Prophet模型较无特殊任务Prophet模型和ARMA模型能够更好地拟合特殊任务消耗数据，拟合效果好。利用均方差、平均绝对误差、绝对误差、平均绝对百分比误差4种常用的预测模型精度评估指标[11]，对3种预测模型的精度进行对比，结果如表6所示。

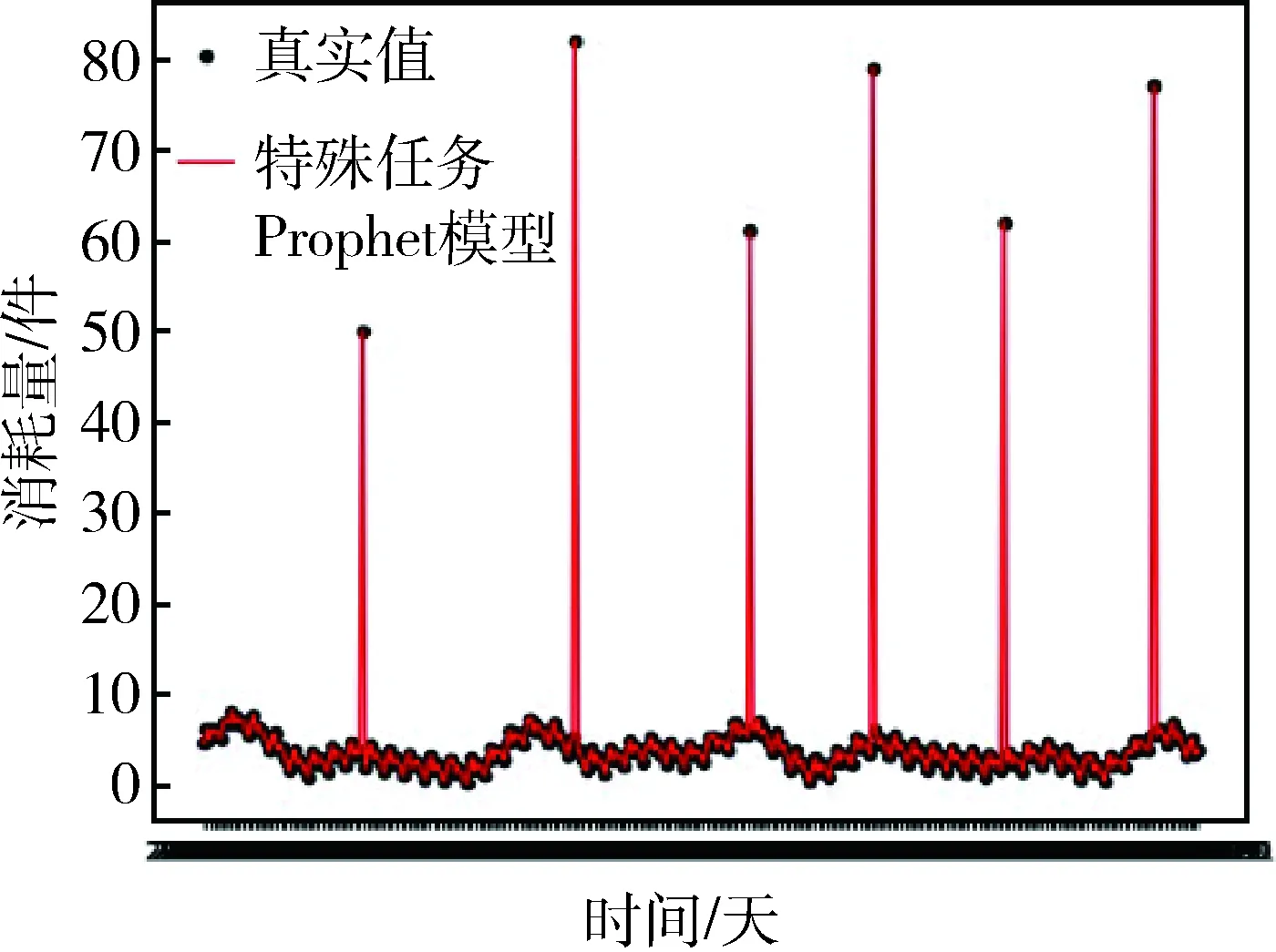
图5 考虑特殊任务的Prophet模型的拟合曲线

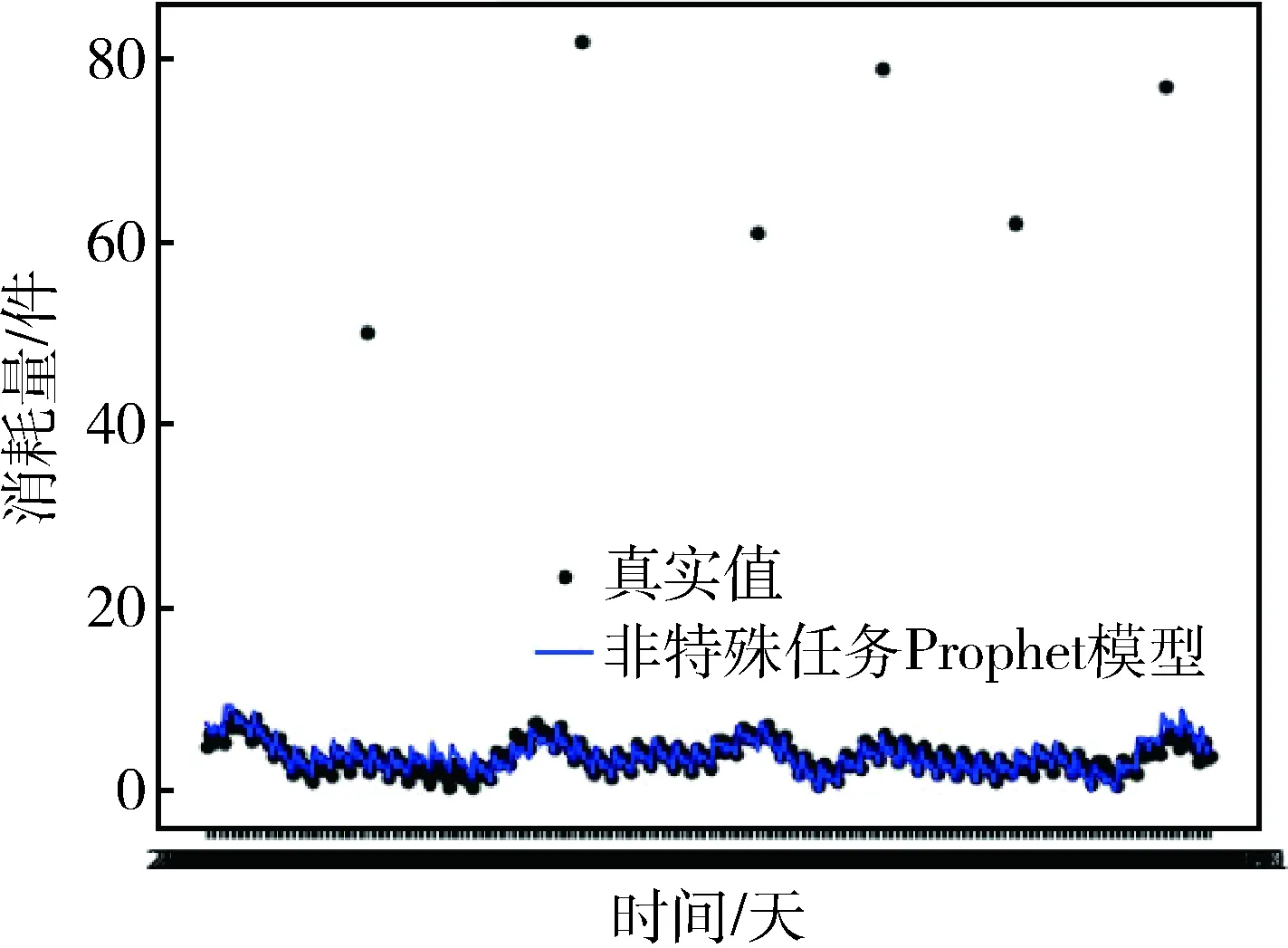
图6 无特殊任务Prophet模型的拟合曲线

图7 ARMA模型的拟合曲线

表6 3种预测模型的拟合精度对比

由表6可以得出：考虑特殊任务的Prophet模型相较于无特殊任务Prophet模型和传统时序预测模型，预测误差小、精度高，对目前特殊任务下的航材消耗规律具有较好的适应程度，更加符合航材消耗的实际情况。

4 结论

考虑特殊任务的Prophet模型对特殊任务条件下的航材消耗规律具有良好的适应性，应用该模型进行特殊任务下航材时序消耗预测具有极强的针对性和有效性。在目前大项任务、演习演练频繁，异常消耗数据量大的背景下，该研究成果为解决当前航材消耗量预测方法难以处理特殊任务造成的异常消耗数据，对特殊任务消耗数据拟合和预测效果不佳的问题，提供了新的思路和方法。但该模型仍然是基于单一变量的预测模型，下一步将综合考虑天气、环境和任务等因素，进一步提高预测模型的合理性和预测精度。