基于GM(1,N)模型群的装备维修性及影响因素分析
柯宏发, 马 超, 王乃超, 孙云辉
(1. 航天工程大学航天保障系, 北京 102206; 2. 航天工程大学研究生院, 北京 101416;3. 北京亚美联技术有限公司, 北京 100080)
伴随装备的构成复杂化、结构体系化、认知信息化等发展趋势,在未来战争中只有保持良好的可用性,才能确保装备的战备完好性和任务成功率,充分发挥其作战效能和体系贡献率。装备良好的可用性对装备维修的依赖性日益增大,使装备维修性设计、分析和试验验证工作越来越成为装备研制过程中不可忽视的重要环节[1-3],而这些维修性工程活动的实质问题就是装备维修性建模。
装备维修性建模一般分为定性建模和定量建模,定性模型包括描述性模型[4]、流程图[5]和图解式模型[6]等,定量模型包括计算模型[7-13]和仿真模型[14]等。其中计算模型是各种装备维修性特征参数及变量之间数学关系的抽象表达,是维修性定量分析的重要工具,目前国内在该方面已经取得了诸多研究成果。这些成果大致可分为3类:
1) 维修性参数及其相关关系的数学描述模型。如:朱伟亭[8]论述了反水雷武器装备系统的平均修复时间,系统维修时间与系统维修事件维修时间的关系,维修事件维修时间与相关维修活动时间的关系,维修工时的数学描述4种维修模型;丁定浩等[9]建立了可靠性、维修性、保障性参数指标体系及其组合参数和单项参数的数学模型。
2) 针对维修性水平及其影响因素的分析模型。如:陶凤和等[10]提出了机械系统维修性影响因素集及其量化标准,并建立了系统维修时间及其影响因素回归分析模型。该方法仅是一个单变量的多因素分析模型,无法建立多个维修性变量及其影响因素分析模型。
3) 装备维修性水平评估模型。如:高婉丽等[11]首先运用故障树分析法对系统故障模式进行识别,然后采用矩阵积和式函数计算维修性综合指数对加注系统维修性进行评价;程松等[12]采用矩阵积和式函数评价底层模块化通信开关电源的可维修性;罗旭等[13]提出了一种改进的维修性设计参数综合评价决策方法;董博超等[15]提出了基于Bayes理论的维修性指标评定方法。上述方法实现了维修性水平的整体评估,但难以对维修性水平的影响因素进行分析;且常用的模型基本上是统计模型,需要连续观测较多的样本。
由于受故障模拟、试验经费等主客观条件的限制,高新装备维修性验证试验所观测到的数据量较小,因此建立GM(1,N)模型[16-21]可较好地解决“小样本”“有限知识”数据的分析问题。如:笔者利用GM(1,N)模型对小样本下影响装备性能的电磁环境因素的主次关系[17]和装备维修水平影响因素的主次关系进行了分析[18];袁泉等[19]提出了基于新息优先累积法的GM(1,N)模型,提高了模型的预测精度,并应用于我国水电发电量和广西农业总产值的预测实验;范震等[20]首先运用灰色关联分析法对我国大豆价格的影响因素进行分析,并选择主要的影响因素作为模型的相关因素变量,构建了基于GM(1,N)的大豆价格预测模型。笔者拓展了GM(1,N)模型,针对多个维修性特征及其影响因素建立GM(1,N)模型群,提出了基于GM(1,N)模型群的装备维修性及影响因素分析步骤,并进行了算例分析验证。
1 装备维修性GM(1,N)模型及其参数估计
1.1 装备维修性建模指标选择
装备维修性包括装备设计和制造所决定的固有维修性和装备使用操作人员的技术水平、装备维修保障条件、维修策略等各种因素的综合影响。目前大多数文献均仅侧重于装备维修性水平评估,且在评估过程中将维修性设计水平提升过程与维修性水平评估过程相互割裂,难以实现维修性水平评价和维修性设计提升过程的统一,进而在一定程度上造成了“两张皮”的问题。为使维修性设计提升与水平评价同步并行,需从整体上建立多个维修性特征及其影响因素分析模型,将二者之间的相关性分析、主要因素分析等无缝集成起来,在整个装备研制过程中高度融合和共享,以便于根据维修性水平追溯其影响较大的因素,如维修性环境、维修性设计和维修性保障等。
装备维修性评价包括定性评价和定量评估,笔者选取平均修复时间、平均预防性维修时间、平均维修停机时间、维修工时率等维修性定量评估指标作为装备维修性特征参数。其中:平均修复时间是指修复1次装备故障所需时间的平均值,修复时间越短,装备的维修性越优良;平均预防性维修时间是指装备1次预防性维修所需时间的平均值,时间越短,装备可维修性能越优良;平均维修停机时间是指单位工作时间内所需维修停机时间的平均值,时间越短,装备可维修性越好;维修工时率是指单位工作时间花费的维修工时的平均值,时间越短,装备可维修性越好。
关于装备维修性水平影响因素,笔者选取维修环境、维修性设计因素、人为要素、保障要素等。其中:维修性环境方面的因素包括装备运行环境、维修环境等;维修性设计因素包括维修简易性、维修可达性、备件模块化与互换性、拆卸装配性、维修安全性、人素工程、检测性和诊断技术、防差错设计等;人为因素包括人员专业技术水平及其训练等;维修性保障要素包括维修技术文件、备件、工具、设施等。
1.2 GM(1,N)建模数据的等极性化[16]
针对装备维修性及影响因素构建GM(1,N)模型时,为强化各因素间的接近性及增加可比性,需要对原始数列进行等极性化处理,即去掉负极性因子、保留正极性因子,使变换后的数列具有“等权”“等极性”等性质。

(1)
下限效果测度变换为
(2)
适中效果测度变换为
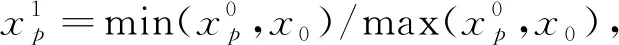
(3)
式中:x0为适中值。
1.3 GM(1,N)模型的参数估计[16]

Xi(1)和Yj(1)分别为Xi(0)和Yj(0)的1阶累加生成算子数列,Zi(1)为Xi(1)的紧邻均值生成数列,即
(4)
(5)
为针对装备维修性特征参数Xi(0)和维修性影响因素的GM(1,N)模型,式中:参数ai和bij分别为模型的发展系数和驱动系数。
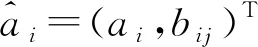
假设中间计算参数
(6)
(7)
则GM(1,N)模型的最小二乘估计参数序列为
(8)
其白化方程(也称为影子方程)为
(9)
式(9)即为装备维修性的N个特征参数及其M个影响因素的GM(1,N)模型群。
2 装备维修性及其影响因素分析
基于影响因素对装备维修性特征的影响程度大小,只考虑GM(1,N)模型群中驱动系数值的大小,则驱动系数矩阵
镇(乡)人民政府及防汛抗旱指挥机构具体承担本辖区内山洪灾害防御工作,督促镇(乡)和村、组开展雨情、水情的日常监测预警、应急处置、抢险救灾、宣传培训、防灾演练等。协助上级主管部门开展汛前排查、汛中检查、汛后核查,做好山洪灾害防御有关资料和预案修订、危险区划定等汇总、上报和年度工作总结。
(10)
基于驱动系数矩阵B可分析装备多个维修性特征与影响因素的主次关系,具体方法如下:
1) 考察装备维修性特征Xi(i=1,2,…,N)的影响因素,记
(11)
则装备维修性影响因素Yj*对装备维修性特征Xi的影响最大。
2) 若存在v,l∈{1,2,…,N},满足
(12)
则称所有装备维修性影响因素对装备维修性特征Xv的影响大于维修性特征Xl,并记为Xv≻Xl,即维修性特征Xv对影响因素的适应性比Xl强。若对于∀l=1,2,…,N,l≠v,恒有Xv≻Xl成立,则称Xv为最优维修性特征,即装备维修性特征Xv对影响因素的适应性最强。
3) 若存在w,g∈{1,2,…,M},满足
(13)
则称装备维修性影响因素Yw对所有装备维修性特征的影响大于因素Yg,记为Yw≻Yg。若∀g=1,2,…,M,w≠g,恒有Yw≻Yg成立,则称影响因素Yw对装备维修性特征的影响最小。
4) 若存在v,l∈{1,2,…,N},满足
(14)
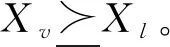
5) 若存在w,g∈{1,2,…,M},满足
(15)

对于具有N个维修性特征参数和M个维修性影响因素的装备维修性分析系统,未必有最优维修性特征和最小影响因素,但是一定会有准优维修性特征和准优影响因素。
3 算例分析
设在某型指控装备的维修性考核试验活动中,装备的平均修复时间、平均预防性维修时间、平均维修停机时间及维修工时率的数列分别为
由于4个时间性指标均为极小值极性,进行等极性化处理后可得
维修性环境的复杂程度、维修性设计水平、人员能力水平、维修性保障水平的数列分别为
其中环境复杂程度为极小值极性,其他3个为极大值极性,进行等极性化处理后可得
依据GM(1,N)建模及其参数估计算法,得到该型装备维修性4个特征参数及其4个影响因素的GM(1,N)模型群为
驱动系数矩阵

基于矩阵B,可得如下结论:
1) 根据各行的最大值可知:对该型装备平均修复时间影响最大因素的是维修性环境的复杂程度,对平均预防性维修时间影响最大的因素是设计水平,对平均维修停机时间影响最大的因素是维修性保障水平,对维修工时率影响最大的因素是维修性保障水平。
2) 根据各列的最大值可知:受维修性环境复杂程度影响最大的特征是该型装备平均修复时间,受设计水平影响最大的特征是该型装备维修工时率,受人员能力水平影响最大的特征是维修工时率,受维修性保障水平影响最大的特征是维修工时率。
3) 根据每行求和的最大值可知:维修工时率是该型装备的准优维修性特征,准优特征次序依次为维修工时率、平均修复时间、平均预防性维修时间和平均维修停机时间。
4) 根据每列求和的最大值可知:维修性保障水平是该型装备维修性特征的准优影响因素,准优影响次序依次为维修性保障水平、设计水平、人员能力水平和维修性环境的复杂程度。
需要说明的是,笔者通过算例分析得到的结论仅仅是针对该型装备的维修性特征及其维修性水平影响因素数据,准优特征次序和准优影响次序并非装备维修性的普遍特性。
4 结论
装备维修性水平是设计出来的,分析装备维修性特征及其水平影响因素的主次关系,可有效地改进维修性设计中的薄弱环节,进而提高装备维修性水平。但是基于经典统计方法的装备维修性水平验证与分析需要较多的数据样本,目前的实际工程背景难以满足需要。笔者根据装备维修性分析的数据少、不确定性多等特点,提出了基于GM(1,N)模型群的多维修性特征、多影响因素分析方法。通过算例分析表明:该方法能从多个角度对装备维修性特征及影响因素进行综合分析,不仅能分析每种装备维修性特征影响因素的主次关系,还可分析装备维修性的准优特征次序关系、装备维修性水平影响因素的准优影响次序关系等。该方法有利于抓住影响装备维修性水平的多种次序关系,对改进提高装备维修性水平具有重要的工程应用价值。另外,由于传统GM(1,N)模型难以准确地描述系统特征的变化规律[21],笔者仅通过驱动系数矩阵进行了分析;下一步将考虑发展系数矩阵对装备维修性特征及其水平影响因素进行深入研究。

