基于链路随机打击的后勤保障网络毁伤过程研究

邓 群

(陆军勤务学院油料系， 重庆 401331)

与计算机网络、社交网络、交通网络等其他复杂网络不同，后勤保障网络隐含的战争背景，意味着其可能面临更多频繁的主动攻击，而非偶尔的自然灾害或不可预料的系统风险。当后勤保障网络遭受外部攻击时，网络内部的各个要素会主动地相互协同，进而完成系统修复，在这一过程中包含了大量的非线性相互作用，甚至还有可能在宏观层面发生涌现现象。

随着复杂网络理论的兴起，后勤保障领域相关研究逐渐从以往对保障体系的定性论述深入到对保障网络的定量分析。其中，作为评判复杂网络的关键指标，抗毁性始终是后勤保障网络研究的重要课题之一。近年来，学术界关于复杂网络抗毁性的理论成果日益丰富完善，相关研究的焦点主要集中在2个方面：一是关于网络节点[1-3]与链路[4-6]的针对性研究，其本质上是对复杂网络组成要素的度、介数或其他改进指标的考察[7-10]，通过对比不同节点或链路失效对网络的影响，实现对其重要性的评判；二是对复杂网络级联失效[11-13]的探讨，其核心思想是从一个动态的系统性视角，以复杂网络的连通度为落脚点[14-15]，更加注重分析由节点或链路失效导致的连锁反应，进而从不同攻击策略[16-17]、不同负载方案[18]以及不同信息条件[19]等角度对复杂网络抗毁性研究加以细化和深入。

总体来看，复杂网络抗毁性研究从理论上进一步揭示了现实世界网络系统的规律和特性[20-22]，但仍存在几点不足：一是大多数研究单纯考虑网络损毁，忽略了网络节点与链路的修复重建，导致研究结果相对单调、片面，具有较强的主观倾向；二是对于网络节点与链路的刻画过于简单，往往认为节点“非有即无”、链路“非通即断”，很少考虑网络要素不完全损毁的情况，相关模型描述过于苛刻，与实际情况存在一定偏差；三是部分研究必须以假定网络无限大为前提，否则很难凸显复杂网络的特性，而现实世界中很多网络是有限规模的，这就使得部分理论成果转化应用效果不尽理想。此外，复杂网络组成要素间关系复杂，难以从宏观角度加以描述，以往相关研究大多数采用具体的实(算)例网络对提出的技术方法进行验证，缺乏对复杂网络共性规律的认识。

综上所述，笔者以链路随机打击下的后勤保障网络毁伤过程为研究对象，运用系统动力学方法，结合复杂网络特点，重新审视后勤保障网络抗毁性，旨在探索简单拓扑规则下后勤保障网络毁伤过程的规律特点，从而为复杂网络抗毁性研究提供新的思路。

1 后勤保障网络毁伤过程的动力学描述

1.1 后勤保障网络模型

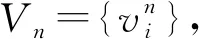
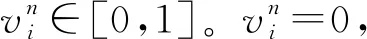
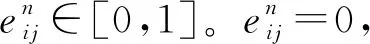
令Y表示后勤保障网络的状态(0≤Y≤M)，其中M为后勤保障网络中链路总数。Y=M，表示网络状态完好；Y=0，表示网络被彻底摧毁。限于篇幅，本文假定网络中所有节点始终完好，即不考虑对网络节点的打击。由此可知，若单纯考虑针对网络链路的毁伤，则某时刻后勤保障网络的状态

(1)

1.2 保障链路毁伤模型

对网络链路的持续摧毁行为从形式上可分为2类：1)当敌方军事优势明显时，可从始至终对后勤保障网络保持一定强度的打击。此种摧毁行为可抽象为持续按数量m去除链路(式(2)、(4))，即每一轮打击均从剩余未被完全摧毁的链路中去除m条链路；2)当敌方军事实力并不明显占优时，则难以长期保持较高的打击强度。此时，可将摧毁行为抽象为持续按比例α去除链路(式(3)、(4))，即未被完全摧毁的链路在每一轮打击中被去除的概率恒为α。

(2)

对于持续按比例α去除链路的摧毁行为，链路被摧毁的概率

Pn=α。

(3)

(4)

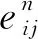
1.3 保障链路修复模型

(5)

(6)

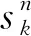
为使模型更加贴近实际，本文特别提出2点假设：

1) 每个完好节点同一时间只能对一条受损链路实施修复；

2) 每条受损链路同一时间只能由一个完好节点实施修复。

2 后勤保障网络毁伤过程的动力学仿真

限于篇幅，本文仅讨论基于持续按数量m去除链路的毁伤过程。如前文所述，后勤保障网络毁伤过程主要取决于2个参数，即打击强度m与修复速率ψ。

2.1 构造网络

后勤保障网络相对稀疏[23]，其中大部分节点的度相对较小，极少出现度很大的节点。由此，本文主要考察ER随机网络(Erdös-Rényi Network,ERN)[24]与WS小世界网络(Watts-Strogtz Network,WSN)[25]形式的后勤保障网络在毁伤过程中的动力学行为。为便于分析比较，本文针对ERN和WSN小世界网络分别构造2个平均度不同的全连通网络作为仿真算例。算例网络及度分布如图1所示，其基本参数如表1所示。

2.2 不同打击强度下的毁伤过程

建立由状态空间Y∞和参数空间m构成的坐标系，绘制出保障网络毁伤过程终态链路变化的轨线图，从而考察不同打击强度对油料保障网络毁伤过程的影响。

针对图1所示的4个网络算例，令m∈{0.001x|0≤x≤1 000,x∈Z}，对于参数m的每个取值，均以Y0=M、ψ=0.5为初值。根据式(2)-(6)将模型迭代2000次，舍弃前1000个迭代值，

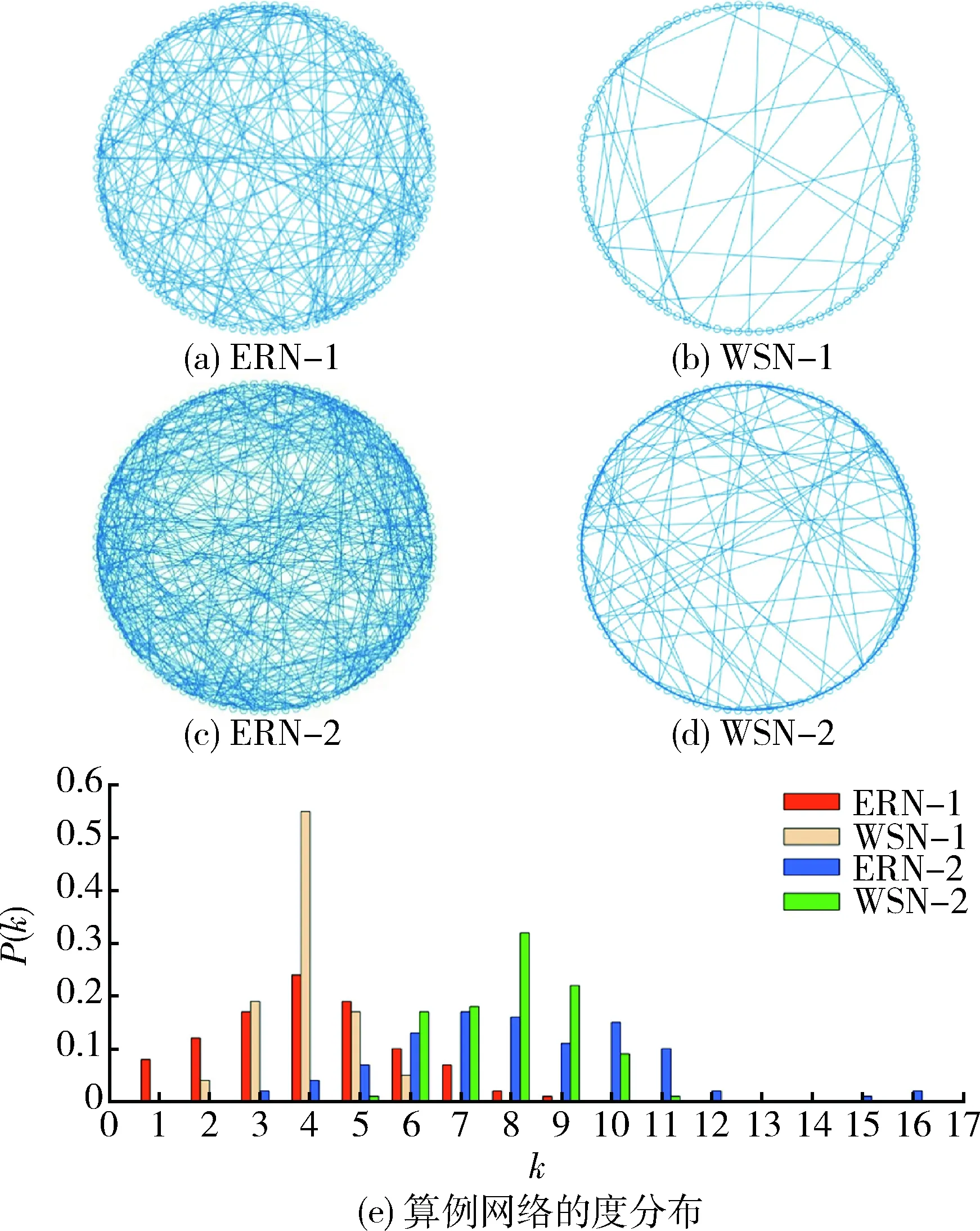
图1 算例网络及其度分布

网络算例NMKLCERN-11002044.083.410.04WSN-11002004.004.260.21ERN-21004068.122.410.08WSN-21003947.882.770.27

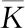
并将Yn后续的迭代值全部绘制到参数m对应取值的纵方向上，即可得到不同打击强度下后勤保障网络毁伤过程终态的变化情况。

本文将每组仿真实验的后1 000次迭代结果的集合视为后勤保障网络毁伤过程的终态，即Y∞={Yi|i>1 000}。若毁伤过程收敛，则Y∞为包含一个或少数几个邻近元素的点集；若毁伤过程相对复杂，则Y∞中将存在更多的元素，并且点集Y∞往往具有较大的直径。不同打击强度下后勤保障网络毁伤过程终态轨线图如图2所示。

2.3 不同修复速率下的毁伤过程

建立由状态空间Y∞和参数空间ψ构成的坐标系，绘制出后勤保障网络毁伤过程终态链路变化的轨线图，从而考察不同修复速率对后勤保障网络毁伤过程的影响。

针对图1所示4个网络算例，令ψ∈{0.001x|0≤x≤1 000,x∈Z}，对于参数ψ的每个取值，均以Y0=M、m=0.15M为初值(不同网络初始链路数M的取值详见表1)。根据式(2)-(6),将模型迭代2 000次，舍弃前1 000个迭代值，并将Yn后续的迭代值全部绘制到参数ψ对应取值的纵方向上，即可得到不同修复速率下后勤保障网络毁伤过程终态轨线图，如图3所示。

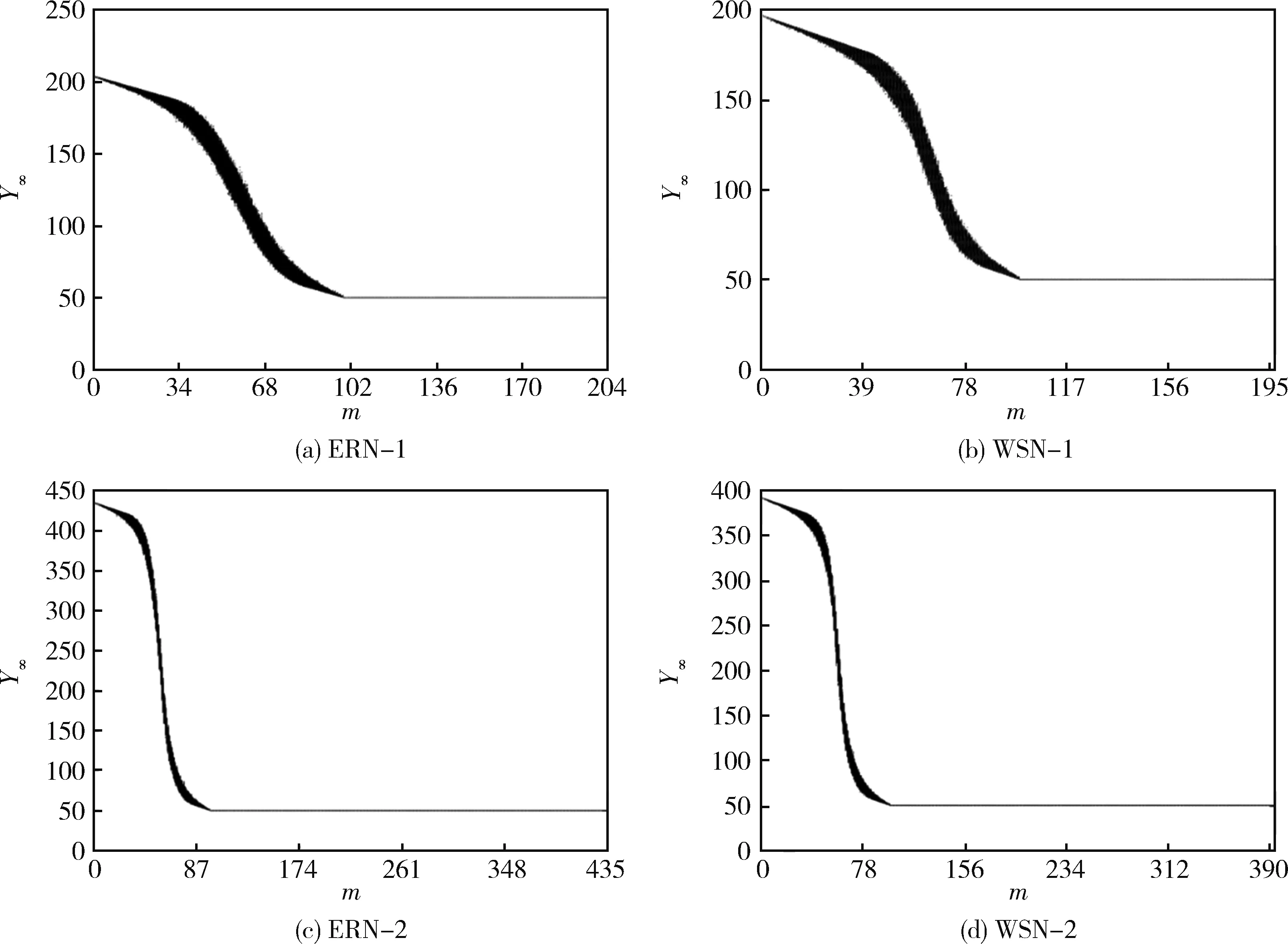
图2 不同打击强度下后勤保障网络毁伤过程终态轨线图

需要说明的是，由式(2)可知针对后勤保障网络毁伤过程的模拟仿真存在一定的或然性，为尽可能减小极端情形对计算结果的影响，将上述实验重复10次，并将结果叠加绘制在其各自对应的轨线图上。

3 后勤保障网络毁伤过程的动力学分析

如图2所示，不同打击强度下后勤保障网络毁伤过程的轨线图相对简单。当打击强度较小时，后勤保障网络终态能够保持较高的完整度；随着打击强度的逐步增大，能够清晰地观察到轨线图中出现拐点；此后，轨线图纵向波动范围扩大，轨线总体呈现快速下降的趋势；当打击强度继续增大，轨线图开始趋于平缓，轨线纵向波动逐渐减小，最终收敛于下限Ymin。根据1.3节提出的2点假设，后勤保障网络状态轨线图下限值取决于网络规模与相邻节点对受损链路的修复能力，即Ymin=N·ψ。由表1可知：各算例网络规模均为100，链路修复速率均为0.5。因此图2中各后勤保障网络状态轨线图下限均为Ymin=50。

可见，当针对链路进行随机打击时，后勤保障网络在不同打击强度下的毁伤过程轨线图比较符合主观预期。这是因为链路的修复与链路自身无关，而是主要取决于受损链路的相邻接点。由于本文在模拟网络链路毁伤的过程中始终假定网络节点全部完好，故此时后勤保障网络毁伤过程的动力学特征并不复杂。

然而，不同修复速率下的后勤保障网络毁伤过程则呈现出完全不同的动力学特征，如图4所示。由图4可知：不同修复速率下毁伤过程的轨线不再平滑，轨线图中存在明显的阶跃行为。对于定义域内的某些特定取值(即阶跃点)，修复速率的微小变化将会对后勤保障网络毁伤过程产生较大影响。然而，当修复速率在相邻阶跃点之间移动时，后勤保障网络毁伤过程的总体变化却并不显著。

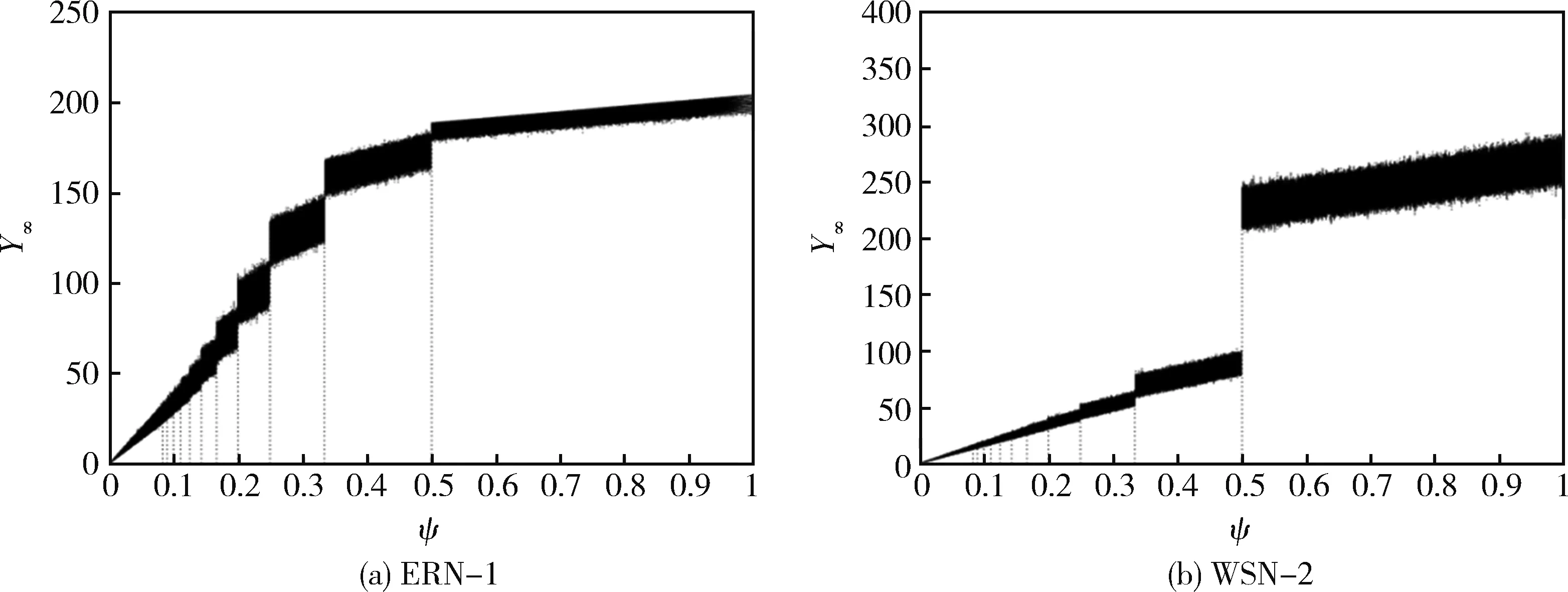
图4 不同修复速率下后勤保障网络毁伤过程的阶段性特征

进一步考察图4不难发现:各阶跃点的横坐标恰为0.5，0.33，0.25，0.2,…，即1/n(n>1)。随着n的逐渐增大，阶跃行为的间隔按照1/[n·(n-1)]的规律迅速收窄，毁伤过程的阶段性特征愈发模糊，在轨线图上则体现为修复速率越小，毁伤过程终态的轨线越平滑。

阶跃点横坐标表现出显著的幂次规律，意味着后勤保障网络毁伤过程的阶段性特征并非偶然。尽管从微观层面上看，针对链路的模拟打击具有较大的随机性，并且对链路的修复主要是基于节点主观的个体行为而非全局性的统筹协调。但是，包含了大量复杂非线性行为的毁伤过程却在宏观层面上产生了极为规律有序的动力学特征，即非线性动力学系统的涌现现象。

4 结论

本文通过大量模拟仿真，从理论上刻画了基于链路随机打击的后勤保障网络毁伤过程的完整轨迹，揭示和论述了毁伤过程中可能存在的动力学行为及其特征。提出了在不同修复速率下后勤保障网络的毁伤过程存在阶跃行为，并且阶跃点的分布具有显著的幂次规律，这对进一步加强我军后勤保障网络建设，提升战时后勤保障能力提供了理论依据和启示。不过，相关结论只是基于持续按数量去除链路的完全随机攻击模式得到的，并且未考虑网络节点同时遭受毁伤的情形。事实上，信息条件、打击策略、协同规则、节点与链路重要度差异等都将对后勤保障网络毁伤过程带来较大影响，这些也有待于进一步的深入研究。