主动悬架多时滞补偿的一般方法

张进秋， 姚 军， 刘义乐

(陆军装甲兵学院车辆工程系， 北京 100072)

与1/4悬架模型和1/2悬架模型相比，整车悬架模型与真实车辆悬架系统更为接近，其中7自由度悬架模型为最简单的整车悬架模型[1]。7自由度悬架系统包括车体垂直振动、俯仰振动和侧倾振动，基本考虑了真实车辆的运动状态。为了尽可能保持车辆的稳定性，受控悬架系统得到广泛研究[2-4]，其中：BREZAS等[5]利用LQG控制器对整车进行控制；MORADI等[6]设计了一种自适应PID滑模容错控制，并与传统滑模进行了对比，结果表明此控制器控制效果很好；SHIN等[7]利用H∞控制器对火车进行了整车控制。在车辆姿态控制方面，PARIDA等[8]通过引入伺服作动器，用于改变车辆左右的高度，从而保持车辆的稳定性；ANUBI等[9]通过改变悬架连接点的位置实现变刚度，结果证明这一方法相比传统控制方法能降低50%侧翻几率；HU等[10]和KANCHWALA等[11]将主动悬架和主动转向系统结合起来以保持车辆的稳定性。

整车悬架控制目标增加，同时控制约束也更少，体现在可以进行预测控制，即利用前轮或安装在车体前面的传感器采集路面信息，对后悬架进行预测控制。GOHRLE等[12]利用摄像头对车前路面信息采集处理后，对全车进行控制，能有效解决延时的问题，YOU等[13]虽然采用了简单的“on-off”控制，但由于增加了预测技术，因而控制器性能得以大幅提高；MICHAEL等[14]利用预测控制，将半主动控制做成类似主动控制的效果，对于低频的激励具有明显的抑制作用；RIOFRIO等[15]利用Kalman滤波预估了路面信息；WANG等[16]采用了鲁棒预测控制。与普通的控制算法相比，预测控制的效果更为理想。

尽管上述研究取得了大量成果，能明显改善车体行驶平顺性，尤其是预测技术可以更进一步提高控制效果。然而，对于多轮车辆[17-19]，每一个悬架的延时是不相等的。预测技术不能解决不相等延时这一问题。此外，预测技术本身也存在不准确的问题，如传感器采集数据不准确，或采用前轮采集路面信息意味着前轮的时滞没有解决，前悬架没有处于预测控制下。针对这一问题，笔者试图解决多轮车辆每个受控悬架时滞不相等这一问题，以进一步提高车辆稳定性。

1 多轮整车主动悬架数学模型

图1为多轮整车主动悬架模型。

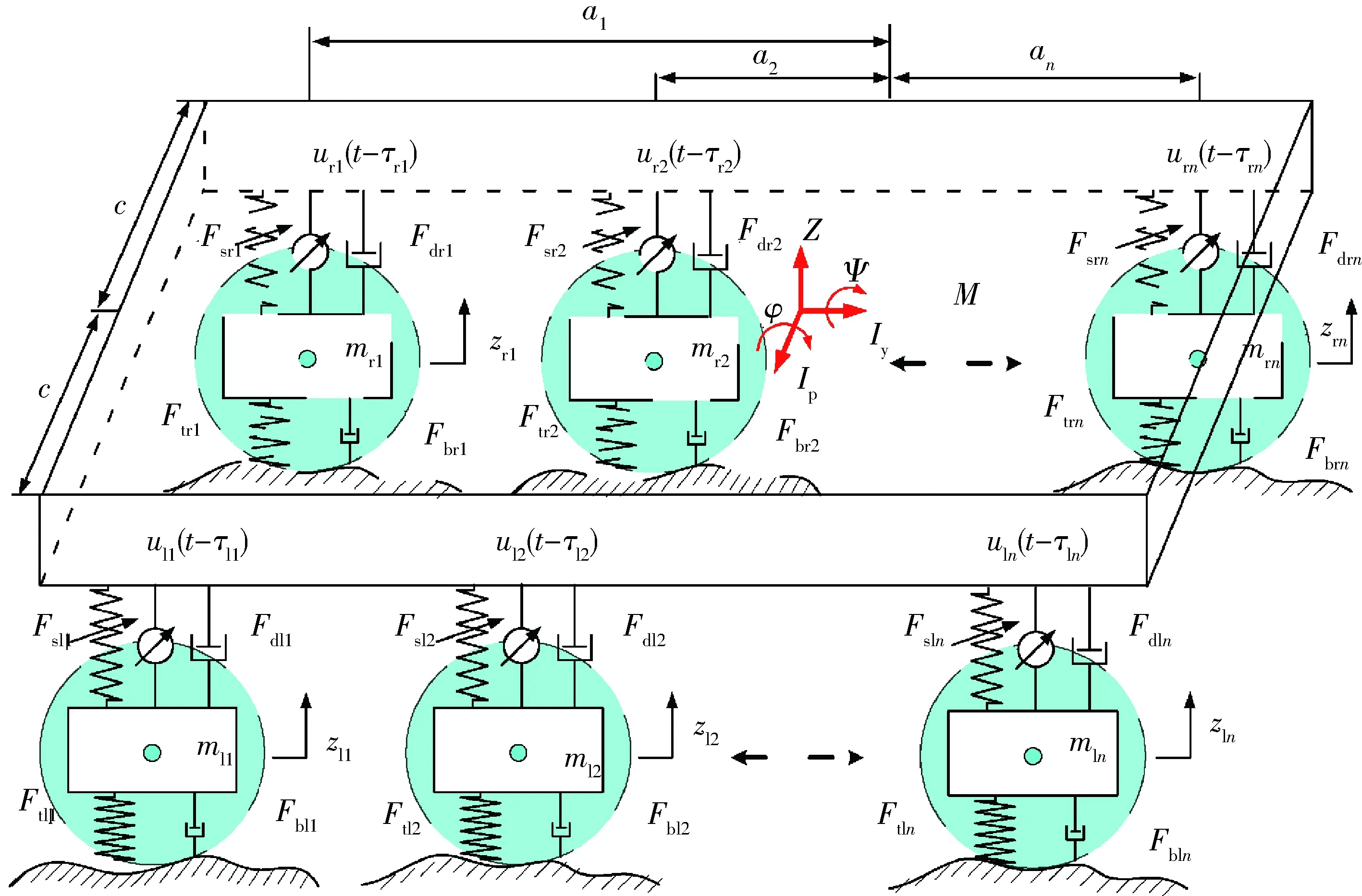
图1 多轮车辆主动悬架模型

图中：

1) 车身质量和载客质量等效为悬置质量M，纵向转动惯量为Ip，横向转动惯量为Iy，且质量和转动惯量均随着M的不同在小范围内变化，具有上下界；左/右侧的车轮质量、刹车系统及其他连接质量分别等效为非悬置质量mli、mri(i=1,2,…,n)。

2) 悬置质量与非悬置质量通过弹簧和减振器连接，其左、右侧作用力分别为Fsli、Fdli(i=1,2,…,n)和Fsri、Fdri(i=1,2,…,n)；非悬置质量支撑在地面上的左、右侧等效力分别为Ftli、Fbli(i=1,2,…,n)和Ftri、Fbri(i=1,2,…,n)。

3) 主动悬架中，左、右侧作动器产生主动控制力分别为uli(t-τli)、uri(t-τri)(i=1,2,…,n)，可用于改善乘坐舒适性，其中t为时间，τri为延时时间。

4) 每个悬架中心到悬置质量质心的纵向距离为ai(i=1,2,…,n)，横向距离为c。

5)z、zli和zri分别为车体和左右车轮的垂直位移；φ和ψ分别为车体的俯仰位移和侧倾位移。

根据牛顿第二定律，多轮整车主动悬架模型的动态方程为

(1)

式中：

Ftli(t)=kuli(zli(t)-qli(t)),i=1,2,…,n;

Ftri(t)=kuri(zri(t)-qri(t)),i=1,2,…,n;

其中：qli和qri分别为左、右地面起伏位移，cli和cri分别为左、右悬架阻尼；kli和kri分别为左、右悬架刚度,culi和curi分别为左、右车轮等效阻尼，kuli、kuri分别为左、右车轮等效刚度。

(2)

式中：θ1=1/M，θ2=1/Ip和θ3=1/Iy均为可变参数，可随M发生变化，满足

θp∈νi={θ:θpmin≤θp≤θpmax},p=1,2,3。

(3)

1.1 实时控制器设计

定义跟踪误差为eh=xh-xhr(h=1,3,5)，其中xhr(h=1,3,5)为参考信号，连续可导，则有

(4)

选择xh+1(h=1,3,5)为式(4)的虚拟控制输入，其理想函数为x(h+1)o，则定义跟踪误差

eh=xh-xho,h=2,4,6。

(5)

将式(5)代入式(4)，可得

(6)

对式(5)求导，可得

(7)

选择理想函数

(8)

式中：kh(h=1,3,5)为一正常数。

定义

(9)

定义自适应率

(10)

式中：

对于主动控制力，满足

A3×2nu2n×1=B3×1,

(11)

式中：

B3×1=

方程(11)存在2n-3个解。不失一般性，不妨设其通解为

(12)

式中：kh(h=2,4,6)为一正常数。

考虑备选Lyapunov函数

(13)

对式(13)求导，并代入式(5)-(8)、(10)、(12)，可得

(14)

整个无时滞补偿控制器(multi Backstepping Adaptive Controller,mBAC)的结构如图2所示。

1.2 多时滞补偿控制器的设计

对于多轮车辆，每个悬架的作动器延时不相等。预测控制技术并未考虑作动器本身的延时，更未考虑每个作动器的延时不相等。由此，需要对上述的实时控制器进行改进。

对误差e2、e4、e6进行补偿，则有

(15)

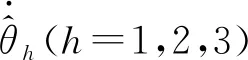
选择Lyapunov备选函数

(16)

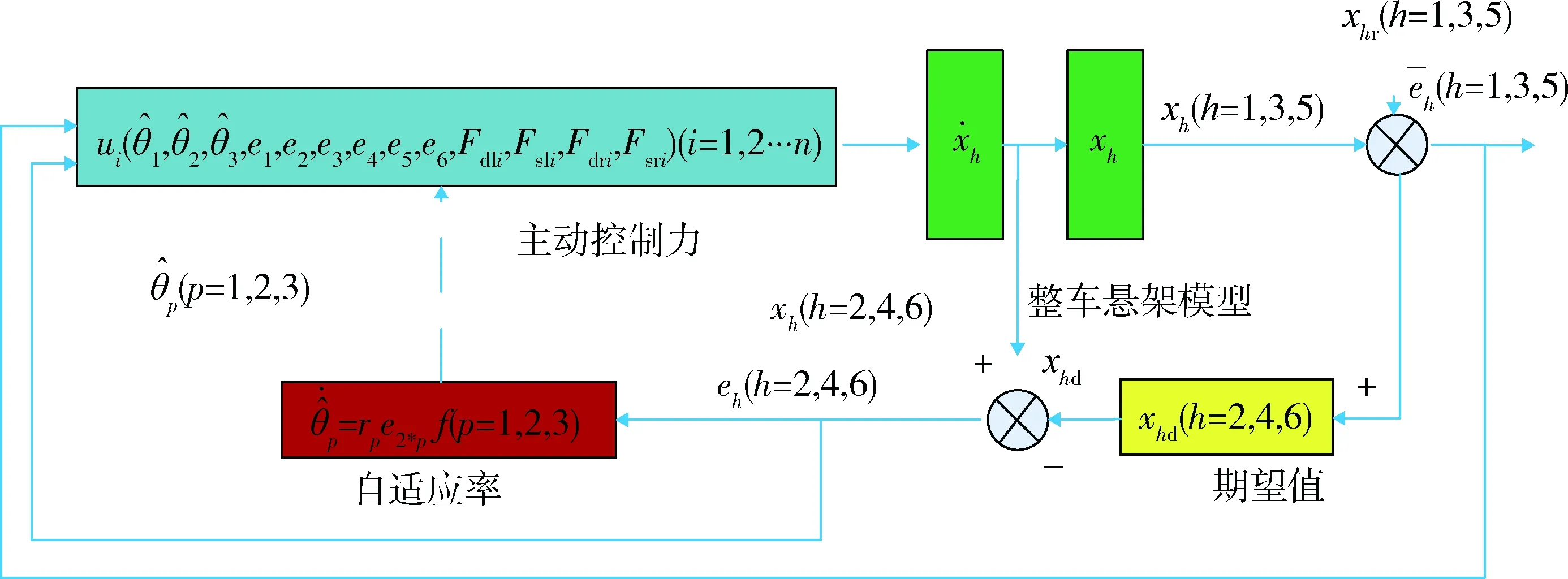
图2 无时滞补偿控制器

根据不等式性质,可得

(17)

对式(16)求导,可得

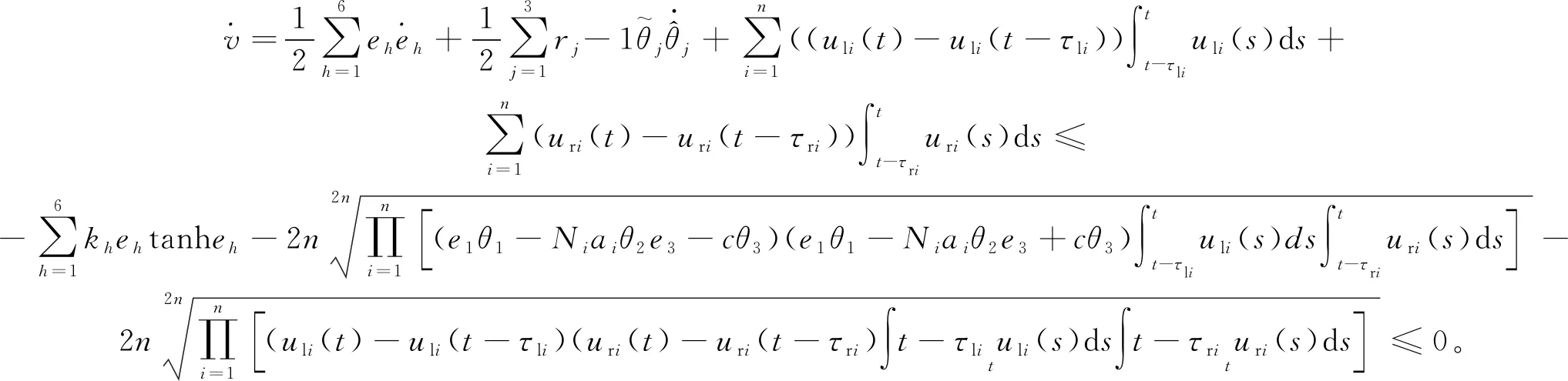
(18)

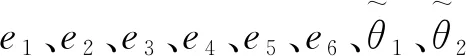
具有时滞补偿控制器(multi-Backstepping Adap-tive Controller with Compensator,mBAC-C)结构如图3所示。

图3 具有时滞补偿控制器结构

2 仿真验证

多轮车辆悬架系统最简单的模型是当n=2时，多轮车辆简化为4轮车辆。对于4轮车辆主动悬架的控制，能反映所设计的控制器的性能。整车悬架模型参数如表1所示。控制器参数如表2所示。

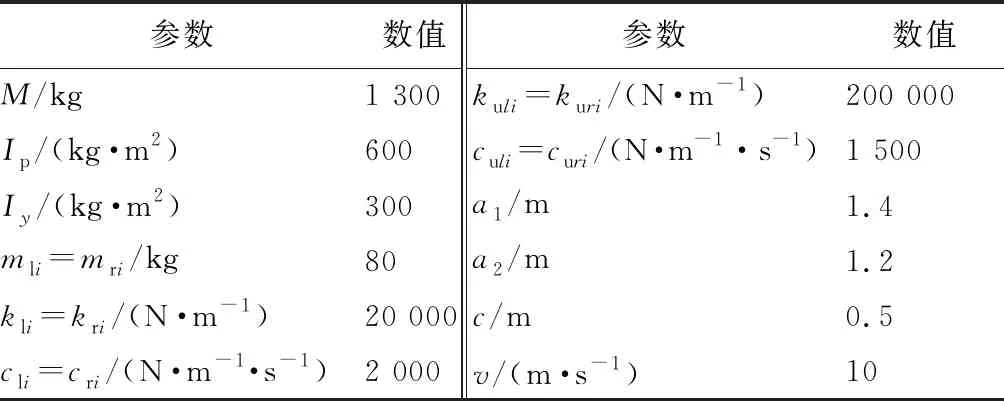
表1 整车悬架模型参数

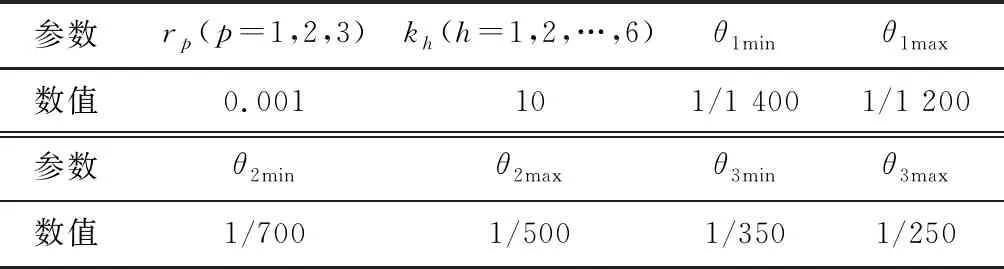
表2 控制器参数

2.1 不等时滞

多轮车辆的每一个主动悬架系统延时往往不同，此处用时滞补偿控制器考察不等时滞对整车的影响。对于相等时滞，τli=τri=0.005 s；对于不等时滞，τl1=0.001 s，τr1=0.003 s，τl2=0.007 s，τr2=0.009 s。车体的垂直加速度功率谱密度(PSD)、俯仰角度功率谱密度和侧倾角度功率谱密度变化曲线对比如图4所示。图中：ED代表相等时滞；uED代表不相等时滞。

由图4可以看出：主动悬架中，时滞不相等时，车身垂直振动加速度和俯仰角度功率谱密度均更大。这说明，不相等时滞会恶化车身振动。实际车辆主动悬架系统的时滞也必然不相等，可以说明预测控制的作用有限。

图4 相等时滞与不等时滞时的功率谱密度对比

2.2 时滞补偿

为了说明时滞补偿的作用，设定整车主动悬架的时滞不相等，即τl1=0.001 s，τr1=0.003 s，τl2=0.007 s，τr2=0.009 s。分别考察主动悬架中无时滞补偿控制器(multi-Backsteeping Adaptive Controller,mBAC)和具有时滞补偿控制器(mBAC-C)以及被动悬架作用下，车体的垂直加速度、俯仰角度和侧倾角度及其功率谱密度变化情况，分别如图5、6所示。

结合图5、6可以看出：

1) 与被动悬架(Passive)相比，主动悬架中车身垂直振动加速度、俯仰角和侧倾角的幅度和功率谱密度变化均较小。这说明主动悬架可以有效降低车身振动。

2) 与被动悬架相比，对于车体的侧倾振动，主动悬架下车身振动幅度更小，但时滞补偿的作用不明显；对于车体的垂直振动和俯仰振动，主动悬架下车身振动幅度更小，时滞补偿作用明显。

上述现象说明，具有时滞补偿的控制器性能明显好于不具有时滞补偿的控制器。

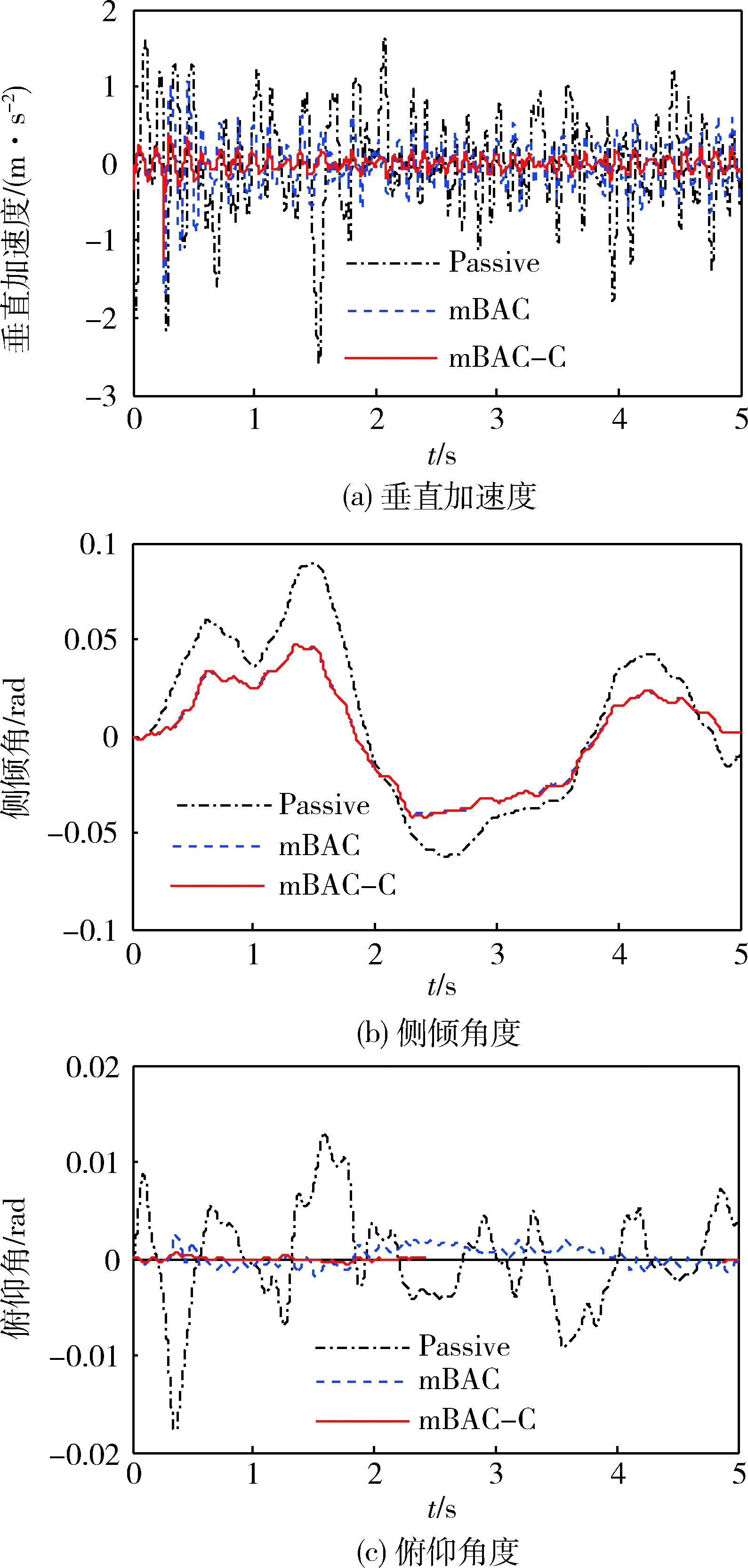
图5 主、被悬架下的控制效果对比

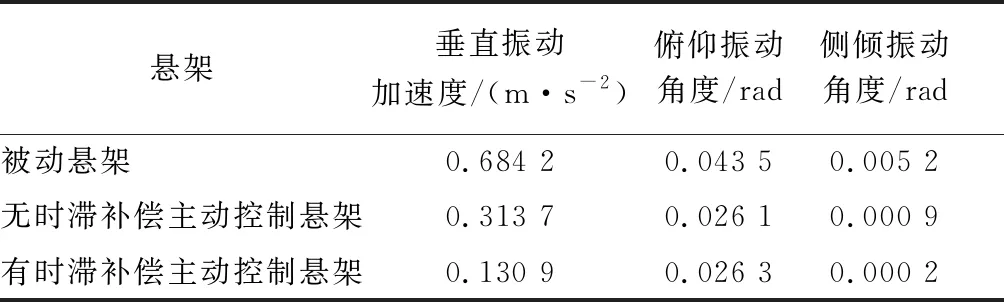
车体振动的均方根值(RMS)如表3所示，可以看出：与被动悬架及无时滞补偿控制的主动悬架相比，具有时滞补偿控制器的主动悬架车身垂直振动加速度及车身俯仰和侧倾角度均更小，说明具有时滞补偿的主动悬架控制器性能更优。

2.3 单位距离时滞的影响

考察单位距离时滞对车体振动的影响。1)车体纵向时滞增大：τl1=0.021 s，τr1=0.021 s，τl2=0.012 s，τr2=0.012 s；2)车体横向时滞增大：τl1=0.021 s，τr1=0.014 s，τl2=0.018 s，τr2=0.012 s；3)普通时滞：τl1=0.014 s，τr1=0.014 s，τl2=0.012 s，τr2=0.012 s。这3种时滞在主动控制器(时滞补偿)下对车体振动的影响如图7所示。

从图7可以看出：

图6 主、被动悬架下的功率谱密度对比

悬架垂直振动加速度/(m·s-2)俯仰振动角度/rad侧倾振动角度/rad被动悬架0.684 20.043 50.005 2无时滞补偿主动控制悬架0.313 70.026 10.000 9有时滞补偿主动控制悬架0.130 90.026 30.000 2

1) 与普通时滞时相比，当车体纵向时滞增大时，车体垂直振动和俯仰振动功率谱密度增大；

2) 当横向时滞增大时，整车振动的功率谱密度变化较小，可以忽略不计；

3) 考虑到车体横向尺寸小、纵向尺寸大，这说明在单位距离时滞相等的情况下，主动悬架中心与车体质心距离越大，时滞作用越明显。

图7 不同时滞下的功率谱密度变化曲线

3 结论

笔者建立了多轮车辆主动悬架模型，设计了无时滞补偿的主动控制器。在此基础上，通过增加时滞补偿器，形成解决主动悬架时滞不相等这一问题的一般方法。对设计的控制器进行了仿真，主要结论如下：

1) 与相等时滞相比，每个主动悬架时滞不相等对车体振动影响更大，更加恶化车体垂直和俯仰振动。

2) 所设计的具有时滞补偿的控制器能解决时滞不相等这一问题，降低车辆振动。这一方法可以处理多轮车辆多时滞问题，具有一般性。

3) 主动悬架中心与车体质心距离越大时，时滞的影响更明显。