基于WorkBench的车辆差速器非圆锥齿轮副静态与模态特性分析

樊智涛， 贾巨民， 王 亮， 陶泽南

(1. 陆军军事交通学院研究生队， 天津 300161； 2. 陆军军事交通学院军用物资配送系， 天津 300161)

差速器是汽车动力系统的重要一环，其性能好坏影响着越野车辆行驶的通过性和越障能力。对普通差速器而言，其齿轮副多为对称圆锥齿轮，在遇到打滑、泥泞等路面时“差速不差扭”的特性使得普通差速器难以实现扭矩的合理分配,车辆常常因动力不足而陷入困境。而限滑差速器的出现使得这一弊端被打破，较大地提高了差速性能。限滑差速器传动结构如图1所示。

目前，对限滑差速器的研究主要涉及改进控制方式和提高限滑性能2个方面，其中对差速器的控制方式主要有强制锁止、机械控制和电动控制3种，而电动控制模式的敏感度和可靠性更高[1]。在提高限滑性能方面主要研究如何提高锁紧系数和越野性能，如：国外托森差速器通过改变传统齿轮副传动，利用蜗轮蜗杆高摩擦传动原理，较大程度地提高了差速器锁紧系数[2]；伊顿公司研制出一种具有锁止功能的新型限滑差速器[3]；姜虹等[4]也进一步研制出三周节变传动比限滑差速器，较大程度地避免了车辆侧滑，提高了车辆越野能力。

图1 限滑差速器传动结构

课题组运用保测地曲率映射原理设计出一种9～12变传动比非圆锥齿轮差速器，该型差速器传动比可变，实测锁紧系数可达到2.2。对该新型齿轮副的研究主要是在传动原理及特性[5]、齿形设计及加工制造分析等方面，而对其轮齿承载能力的研究则相对较少。为进一步验证该新型差速器的性能，应用有限元方法，借助ANSYS WorkBench软件对差速器主要承载件进行强度校核，初步检验轮齿强度能否满足行驶工况要求，并对非圆齿轮副进行模态分析，检验齿轮副在运转过程中的振动和噪声是否会引起共振，最后通过台架对该型差速器能够满足相关力学性能要求等进行了试验验证。

1 几何模型的构建

对于变传动比限滑差速器来说，其核心部件为啮合传动的非圆锥齿轮副。笔者在研究变传动比限滑差速器工作原理的基础上，借助SolidWorks建模软件完成非圆锥齿轮副的模型构建和虚拟装配。

以半轴齿轮为例，半轴齿轮设计为每4个齿为一个周期对称布置，共12个齿，在建模时只建立一个周期的齿廓模型。首先，借助SolidWorks的镜像和圆周阵列得到整体齿廓曲线；其次，按照齿轮大端齿廓曲线到圆心的顺序向球心放样，得到放样曲面，切割外圆球面并与放样曲面生成实体得到初步节锥模型；再次，设定齿宽，采用曲面切除确定小端齿廓；最后，设定中心轴孔直径参数，借助倒角命令对模型做最后处理，完成半轴齿轮的最终建模。行星齿轮的建模方法可参照半轴齿轮进行。

为了更好地反映非圆锥齿轮副模型建立的正确性，还需要进行虚拟装配和干涉检查，如图2所示。装配完成的变传动比非圆锥齿轮副如图3所示。

图2 虚拟装配和干涉检查示意图

图3 变传动比非圆锥齿轮副

2 静力学分析

对变速比限滑差速器而言，车辆在行驶过程中会遇到直线行驶和差速行驶(转弯或限滑)2种工况，选取这2种有代表性的工况进行静力学分析。其中：在直线行驶工况下，差速器处在平衡位置，该情况在车辆行驶过程中出现频率最高；在差速行驶工况下，差速器开始差速限滑，在达到限滑极限(限滑临界点)时差速器所受载荷最大。

2.1 有限元分析模型和算法理论

在齿轮啮合传动过程中，齿面之间会产生摩擦力和正压力。与单件计算和组合计算模型相比，非线性接触摩擦模型能够更真实地反映齿轮受载情况，故选择非线性接触摩擦模型进行分析。

2.1.1 接触摩擦模型

在差速器非圆锥齿轮的啮合传动过程中，齿面间会产生相对滑动，其等价切应力Teg及极限切应力Tlim分别为[6]

τeq=μeqp+b，p≤[τ]；

(1)

τlim=μlimp+b，p>[τ]。

(2)

式中：μeq为等价摩擦因数；μlim为极限摩擦因数；p为单元接触正向压力；b为接触内聚力；[τ]为许用剪应力。当τeq<τlim时，齿轮间就会产生相对滑动。

2.1.2 摩擦接触算法

增强拉格朗日方法对接触刚度系数不很敏感，其能够更好地调节压力的大小，但当出现网格畸形时，需要进行多次迭代，其单元接触压力定义为

(3)

式中：Kn为法向接触刚度；μn为法向摩擦因数；un为法向接触间隙;

(4)

其中λi为第i次迭代拉格朗日乘数。

2.2 前处理及加载求解

根据齿轮副设计要求，选择齿轮副比较常用的20CrMnTi进行仿真分析，其具体材料属性如表1所示。

表1 20CrMnTi材料参数表

在对齿轮副进行网格划分时，采用四面体三维实体单元SOLID187进行非线性计算，网格尺寸设置为1 mm。网格初步划分完成后，为减小计算误差，对齿轮接触面进行网格局部细化，完成细化后的网格如图4所示。行星齿轮共划分为23 384个节点、13592个单元，半轴齿轮共划分为46767个节点、27 183个单元。

图4 齿轮副网格划分示意图

为简化分析过程、缩短分析时间，选取1个行星齿轮和2个半轴齿轮形成齿轮副进行分析，在齿轮副之间添加接触对，行星齿轮为接触面、半轴齿轮为目标面、设定接触类型为摩擦、接触方式为No separation、摩擦因数为0.1。

当车辆以30 km/h 在正常路面直线行驶时，根据车辆参数计算得到此时车轮转速为1 279.42 r/min，壳体所受最大转矩为T=4 929 N·m；当车辆在不同附着路面以同样速度限滑行驶时，给定两侧半轴的阻力矩分别为TR1=1 989 N·m和TR2=2 940 N·m，模拟差速和限滑差扭工况。

2.3 求解及结果分析

参数设置完成后，在求解器中分别计算齿轮副在直线行驶工况和差速行驶工况下的应力和变形值，输出相对应的应力云图和变形云图，分别如图5、6所示。

由图5可知：齿轮副最大应力主要出现在行星齿轮齿顶和半轴齿轮齿根部位，其中直线行驶时最大应力为626 MPa，差速行驶工况时约为660 MPa。与20CrMnTi的强度极限 830～1080MPa 相比，齿轮副强度均能够满足行驶工况要求。

图5 2种工况下齿轮副的应力云图

图6 2种工况下齿轮副的变形云图

由图6 可以看出:2种工况最大变形均发生在行星齿轮和半轴齿轮齿顶部，由于差速工况存在行星齿轮和半轴齿轮的相对转动，其变形量较大，最大变形量约为 0.076 mm；由于直线行驶工况行星齿轮和半轴齿轮无相对转动，行星齿轮起等臂推力杆的作用，其变形较小，最大变形量约为 0.033 mm。以图6(b)中行星齿轮变形量最大的接触面为例，在 Solidworks 中测得其面积为 459.95 mm2,周长为 127.4 mm，变形量远小于上述数值。

综合应力云图和变形云图可以得出:行星齿轮齿顶和半轴齿轮齿根部位容易发生疲劳磨损和点蚀。

3 模态分析

3.1 基本理论

机械系统的每一阶模态具有其特定的固有频率和模态振型，模态分析是进行振动分析的基础。为了避免产生共振，齿轮副的固有频率必须高于其工作频率，而将自身固有频率与外界激励频率间的耦合降到最小，有利于提高其刚度，减小工作负荷，延长使用寿命[7]。

齿轮系统的运动微分方程[8]：

(5)

在对齿轮啮合传动系统的求解过程中,将齿轮系统视为自由振动，即不计外力干扰，且忽略阻尼对振动特性的影响，得到无阻尼自由振动的运动微分方程：

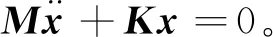
(6)

设x=xsin(wjt)，则可以得到

(K-w2M)x=0。

(7)

3.2 结果分析

理论上齿轮副存在无限个固有频率，固有频率随模态阶数的增加而增大。由于结构振动中高阶模态能量占比太低，对整个结构振动影响不大，一般只对前6阶振型进行分析。且由于齿轮副工作频率一般不会太高，因此激振频率只会和低阶模态的固有频率重合或接近。以差速工况为例,对非圆齿轮副前6阶模态进行分析，其固有振型图如图7所示。

由图7可以看出：在第1阶模态下的最大变形位置主要集中在行星齿轮齿顶处，第 2、4、5阶模态下主要集中左侧半轴齿轮齿顶处，第3、6阶模态下则主要集中右侧半轴齿轮齿顶；在前6阶模态中，模态阶数越高，固有频率越大，其中第 1阶模态下固有频率为 21 677 Hz，第 6阶模态下为26 252 Hz;第 2阶模态的变形量最小，为107.53 mm，第 6阶模态的变形量最大，为165.41 mm。非圆齿轮副齿轮副前6阶固有频率及振型特点如表2所示。

在台架试验时，给定从动电机最大转速为 5 000 r/min，根据转速与频率的关系可知：此时齿轮副最大啮合频率为 83.3 Hz，远小于齿轮副的1阶固有频率，故不会有共振发生。

图7 非圆齿轮副前6阶固有振型

表2 非圆齿轮副前6阶振型固有频率及振型特点

4 加工试验

非圆锥齿轮结构复杂，目前主要有数控线切割、数控铣削以及冷挤压等加工方法，其中：数控线切割加工精度较低，很难实现高精度加工；数控铣削虽然加工精度高，但成本也高，生产效率比较低，不适合批量生产；冷挤压能够制造复杂零件，且效率较高，成本比较低。采用冷挤压方法加工齿轮，加工成型的非圆齿轮副如图8所示。

加工完成后，对变传动比限滑差速器进行台架试验，观察实际工作情况下差速器齿轮副是否会因应力集中导致轮齿折断和磨损，并计算该型差速器的锁紧系数，如图9所示。由于该型差速器为新型限滑差速器，在试验方法上课题组联合吉林大学车辆产品检测实验室共同制定限滑差速器台架试验方法，其步骤为：将差速器装入驱动桥中进行磨合实验，添加适量润滑油，采用风冷方式控制润滑油温度保持在70～90 ℃，运转一段时间后再进行试验。

图8 加工成型的非圆齿轮副

图9 差速器台架试验

设定车轮转速为30 r/min，在两侧半轴分别施加阻力矩100、200 N·m，并计算不同转速差下的锁紧系数值，如表3所示。

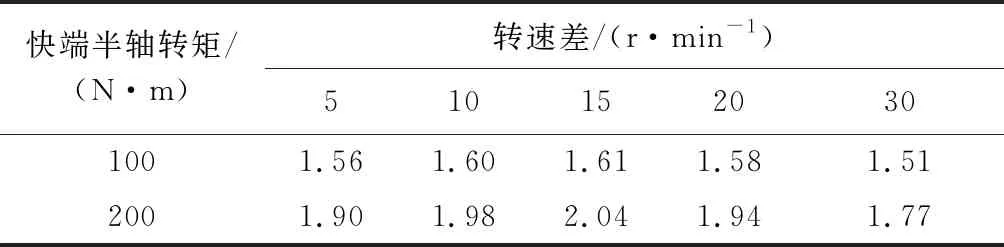
表3 不同转速差下的差速器锁紧系数值

由表3可以看出：限滑差速器的锁紧系数为1.56～2.04。这说明行星齿轮副齿顶和半轴齿轮齿根应力集中部位存在部分磨损，与有限元仿真分析结果相一致，结合试验磨损主要发生部位，可以考虑下一步可在应力集中的齿根处添加加强筋，并对齿形进行鼓形修形处理。

5 结论

借助ANSYS Workbench对变传动比限滑差速器非圆齿轮副进行了静力学和模态分析，主要结论如下：齿轮副应力和变形满足设计要求，最大应力发生在在行星齿轮齿顶和半轴齿轮齿根部位；齿轮副工作时，工作频率远小于固有频率，不会发生共振。