带周期系数的捕食-被捕食模型的相关性质
凌 亚 茹
(南京财经大学 应用数学学院,南京 210023)
0 引 言
随着社会的发展以及生活水平的日益提高,国内外众多学者开始对生态系统、生物资源的研究日益关注,数学家根据生物背景知识,建立相应的数学模型,通过数学方法和计算机模拟来研究和分析对应模型的一些性质和状态,为开发者提供有效的理论参考依据。第一个捕食-被捕食模型于1925年被提出[1]:
随后有许多学者对其进行了研究与改进。而在与渔业相关的捕食-被捕食模型中,水位影响一直受到了国内外许多学者的关注,并对其进行了研究。
1998年,Poggiale[2]研究了不同时间尺度下,空间异质性对单位时间内每个捕食者捕食量的影响。结果表明:密度依赖性迁移在种群总量水平上产生了新的影响,水位的变化,使捕食者与猎物之间的密度产生变化,进而影响捕食数量。
2003年,Coops[3]研究了水位变化在浅水湖生态系统中的作用,结果表明:湖泊水量的显著减少促进了营养关系中更多的相互作用;2005年,Fischer[4]研究了水位变化对湖泊沿岸底栖鱼类群落的影响,结果表明:水位的季节性变化不仅决定了临时淹没区内是否存在物种,而且还可能引发群落结构的复杂变化。
2012年,Moussaoui[5]对欧拉特鱼类群落的结构进行了详细的研究证明,水量的增加阻碍了捕食者捕获猎物,水量减少时,有利于捕食者捕获猎物。结果证实了水对鱼类之间的相互作用产生强烈影响的假设。
2015年,Bouguima[6]研究了3个物种在季节演替下的一种更为复杂的相互作用:
文章通过重合度理论研究周期解的存在性,从生态学角度看:当掠食者攻击猎物时,它可以根据水位获得一定数量的食物。当水位较低时,捕食者更容易接近猎物,r(t)是捕食者捕捉猎物的一个系数,是一个周期的连续函数,它受季节性水位变化的影响,春季到最小值r1,秋季达到最大值r2。此模型广泛描述了水位变化对生态的影响,证明了模型至少存在一个正周期解。
2018年,Moussaouia[7]研究了一种具有新的功能响应的渔业捕食-被捕食模型及其最优收获:
文章主要从持久性和稳定性的角度讨论了系统的动力学特性,得到影响系统持久性的条件。
基于文献[7]的思想和方法,研究如下在捕获条件下带周期系数的捕食-被捕食模型及其最优收获:
(1)
其中a(t)、b(t)、k(t)、q1(t)、E(t)、q2(t)、D(t)、d(t)、e(t)都是以T为周期的光滑函数,q1、q2分别为猎物与捕食者的可捕系数,E(t)为收获效率,b(t)为一个可达到的周期系数,春季达到最小值,秋季达到最大值,e为猎物在生物量上的转化率,d为捕食者代谢消耗生物量的速率,k(t)为猎物的承载力,a为猎物的内在增长率,D(t)是猎物除捕食者外的死亡率。
文章结构如下:第一节利用微分方程上下解理论,给出系统式(1)的周期解存在且唯一的充分条件;第二节讨论模型的动态系统,给出系统持久存在的充分条件;第三节通过极大值理论,给出式(1)在捕获条件下的最优收获策略。
1 周期解的存在唯一性
本节将利用微分方程上下解理论[1]给出式(1)周期解存在且唯一的充分条件。记严格正连续且以T为周期的函数g(t)在(0,∞)上的最大值和最小值分别为gM和gL。
标记:
引理1[8]若方程组
存在一对周期上下解,则在周期上下解之间必存在周期解。

证明首先通过构造模型上下解,从而给出周期解的存在性;再利用做差的方法,得到周期解的唯一性。下证周期解的存在性。
若(xM,yM),(xL,yL)为式(1)的一对上下解,通过微分方程上下解理论可知需满足以下条件:
为满足上述条件,构造(xM,yM),(xL,yL)分别为下述方程组的解:
(2)
(3)
解式(2),利用带入消元法可以得到:
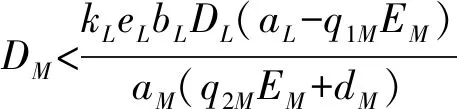
由此可证,(xM,yM),(xL,yL)为式(1)的一对上下解。由引理1可知,式(1)必然存在以T为周期的周期解。下面证明周期解的唯一性。
假设(x1,y1)和(x2,y2)是两对周期解,在[0,T]上满足
xL≤x2(t)≤x1(t)≤xM
yL≤y2(t)≤y1(t)≤yM
且满足
下证x1(t)≡x2(t),y1(t)≡y2(t)的充分条件。
由于
(x1-x2)[(a(t)-q1(t)E(t))-

由x1和x2的周期性,有
(4)
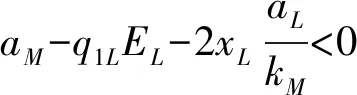
2 持续性与持久性
本节将讨论式(1)持续性与持久性,表明两个物种在捕捞条件下是具有永久共存性的。首先给出持续性与持久性的定义:
定义1 (持续性) 若式(1)的所有解(x(t),y(t))满足:
(i)x(t)≥0,y(t)≥0,∀t≥0;


则式(1)具有强持续性。
定义2 (持久性) 若存在正数m,M,且0 则式(1)具有持久性。 标记 且mi>Mi,i=1,2。 定理2 若mi>0成立,则式(1)是满足持久性的,即对任意的正解(x(t),y(t))都满足: 在证明之前,先介绍一个引理: 证明利用对(1)的放缩,及引理2得到该系统具有持久性。首先证明满足定理2的第一个不等式。 对于任意正的x,y都满足式(1),则有 由引理2可得 对任意的ε1>0,存在实数T1,使得 x(t)≤M1+ε1,∀t≥T1 同理可得 由引理2可得 对任意的ε2>0,存在实数T2>T1,使得 y(t)≤M2+ε2,∀t≥T2 下证定理2的第二个不等式。 由引理2可知 对任意的ε3>0,存在实数T3,使得 x(t)≥m1-ε3,∀t≥T3 同理可得 令t≥T4=max{T2,T3},可得 由引理2可得 则式(1)是强持续的且是持久的,从而保证了两个物种在捕捞的条件下,也是可以长期共存的。 为了求出式(1)的最优收获策略,将利用极大值原理来解决。在参考文献[10,11]的基础上,介绍一个重要的理论。 考虑一个以T为周期的微分方程: 的最优控制,首先引入目标泛函: 并构造哈密尔顿函数: H=g[x(t),t,u(t)]+λf[x,t,u(t)] 其中λ是一个伴随变量,需要满足横截性条件,由最大值原理可知 则最优控制意味着 在本节需要解决两个种群的最优收获策略。首先考虑最大利润的可持续收获问题,可将其归结为如下的一个最优控制问题: 使得 其中:c是单位捕捞成本,p1、p2分别为猎物与捕食者的单位价格,δ为瞬时年折扣率。 应用最大值原理,构造哈密尔顿函数为 H=e-δt(p1q1x-p2q2y-c)E(t)+ 其中λ1,λ2为伴随变量,有式(5): (5) 并且 (6) (7) 可以得到 其中 则有 其中C为任意常数。 当t→∞,时eδtλ1仍然为有界量,满足横截性条件,则C=0,即 由式(6)可得 则λ2也满足横截性条件。 由式(6)与式(7)可以决定最优的平衡解(x*,y*), 则最优捕捞策略为 首先通过定理1给出周期解存在且唯一的条件,从而保证了周期解的稳定性;再提出定理2保证捕食者与猎物能够永久共存,这是生物数学研究的最重要前提,在此前提下,才可以去讨论经济效益;最后给出了在不导致物种灭绝的前提下,能够实现渔业利润最大化的收获策略,保证其所具有的现实意义.


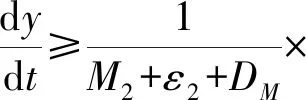
3 最优收获策略
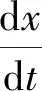

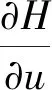

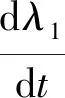
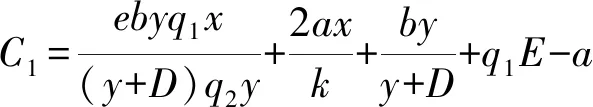
4 结 语

