基于等价销距的铁路限界安全检算算法研究

甄 勇，宁 涛，张英贵

(1. 中国铁路南宁局集团有限公司 信息技术所，广西 南宁 530029 ；2. 中南大学 交通运输工程学院， 湖南 长沙 410075)

近年来，随着国民经济的快速发展和国家基础设施建设的稳步推进，铁路承担的超限货物越来越多，货物外形尺寸越来越大，结构越来越复杂，一旦发生事故救援难度大，严重影响正常运输生产[1]。传统的限界安全检算算法，不仅效率低、出错率高，而且安全风险较大。因此，引入等价销距的概念，设计一种基于等价销距的铁路限界安全检算算法，避免传统方法存在的限界关键控制点信息缺失问题，为超限货物运输安全决策提供技术与方法支撑。

1 等价销距原理及计算方法

1.1 限界安全检算理念

铁路限界是指为确保铁路运输设备设施的运行安全，规定的机车车辆或建筑物、构筑物不准侵入的限制空间[2]。铁路限界安全检算是将货物轮廓与通行径路上的建筑限界轮廓进行比对，并根据比对结果确定限速等运行条件的过程[3]。在比对过程中不论采用区间还是单个设备最小综合建筑限界，其数据都是综合处理后的结果[4]。由于曲线部分的最小建筑限界与装载超限货物的车型和装载方式有关，因而不同车型和装载方式的车辆通过区间或设备时，影响车辆通行的最小控制点位置可能不同。此时，若单纯采用货物轮廓加偏差量与标准车折减后的建筑限界进行比对，很可能会漏掉关键的控制点信息，存在安全隐患。采用缩小建筑限界和基于等价销距的限界安全检算算法，可以有效规避上述安全风险[5]。该方法通过货物偏差量的等价变换，计算出货物通过曲线线路时的内偏差量和外偏差量的等价销距，选择与等价销距相对应的通行径路上的建筑限界数据( 基于整数米销距的折减数据)，计算货物实际轮廓与建筑限界之间的安全距离，做出决策结论[6]。

1.2 等价销距原理及计算方法

当超限车在曲线运行时，因车辆纵向中心线和铁路线路中心线不能重合而产生偏差量；通常情况下，超限车所装运的货物中部会向曲线内侧偏移，端部则向外曲线外侧偏移，由此产生的偏差量细分为内偏差量、外偏差量。货物偏差量可以由一定长度的销距所导致的限界折减量进行换算与衡量，该长度的销距称之为等价销距；在相同的曲线上，采用等价销距计算的限界折减量与货物偏差量等值。

现以《铁路超限超重货物运输规则》[7]中 “普通平车跨装”的内偏差量计算为例，说明等价销距原理及其计算方法，并证明等价销距产生的偏差量与建筑限界在曲线部分的折减计算量的一致性，进一步说明采用缩小限界的方法与《铁路超限超重货物运输规则》中的检算算法等价。实际计算时，可采用《铁路技术管理规程》中建筑限界在曲线部分的加宽公式作为折限界减计算公式[5]。

《铁路技术管理规程》中曲线内侧折减公式可表示为

式中：W内为折算内偏差量，mm ；l为计算车辆中心销距，mm ；R为曲线半径，m ；H为计算点自轨面起算的高度，mm ；h为外轨超高，mm。

《铁路超限超重货物运输规则》中内偏差量计算公式为

式中：C内为内偏差量，mm ；L为跨装支距，mm ；x为货物检定断面至跨装支距中心线的距离，mm。

现说明采用曲线内侧折减公式和内偏差量计算公式计算等价销距，将公式 ⑵ 变形为

可见，曲线部分限界内侧折减量等价于内偏差量。

外偏差量和其他装载方式下的等价计算过程可以依次类推。

经由上述公示推导分析易知：采用缩小限界的方法与《铁路超限超重货物运输规则》中的检算算法等价。内偏差量的等价销距l内，取其计算公式分子部分的平方根；外偏差量的等价销距，有K值的将K值加宽至货物轮廓后，取其计算公式分子部分的平方根。对于多导向货车装运货物的内外偏差量，也可按上述规则处理，与R无关的偏差量加宽至货物轮廓，与R相关的偏差量将分式通分为以R8 为分母的分式，并对分子部分求和，再取分子之和的平方根。在实际应用中，当内、外偏差量不是整数时，采用向上取整的方法，使计算结果有利于保证运输安全[8]。当装载货物的车辆在曲线线路上通过时，针对内偏差量，按照内偏差量等价销距l内的计算结果分别选取左曲线左侧和右曲线右侧数据来计算安全距离。类似地，针对外偏差量，按照外偏差量的等价销距的计算结果分别选取左曲线右侧和右曲线左侧数据来计算安全距离[9]。

2 基于等价销距的限界安全检算算法设计

2.1 安全检算算法分析

限界安全检算的基础在于货物轮廓和建筑限界及其相互位置关系。设A，B为建筑限界上的点，线段AB为建筑限界轮廓，C为货物轮廓上的点，k为AB之间的斜率，k1为AC之间的斜率，k2为BC之间的斜率，xA，xB，xC分别为A，B，C在笛卡尔坐标系中的横坐标值，yA，yB，yC分别为A，B，C在坐标系中的纵坐标值。限界轮廓与货物轮廓的位置关系图如图1 所示。

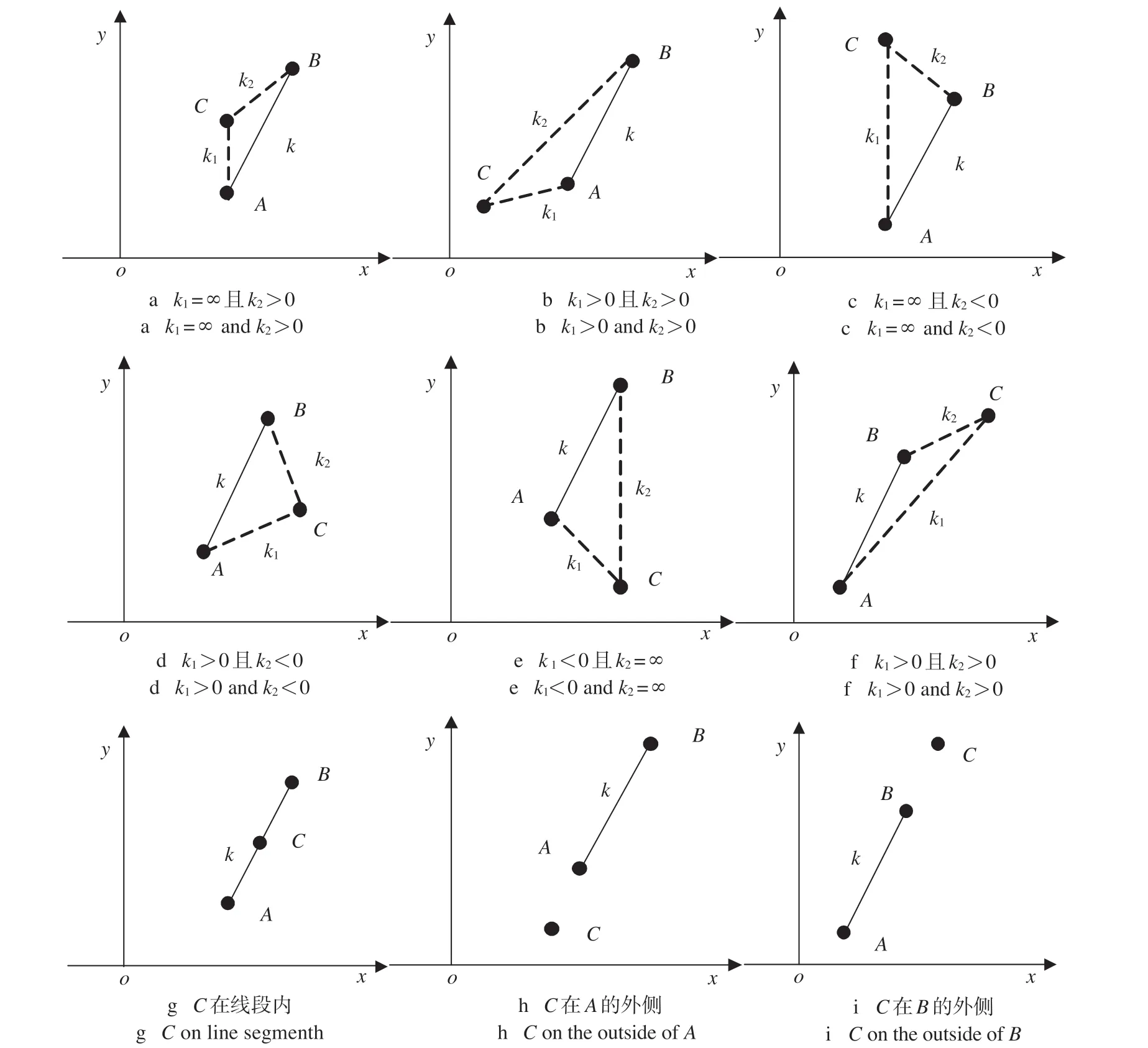
图1 限界轮廓与货物轮廓的位置关系图Fig.1 Location relation diagram of cearance outline and cargo outline

（1）若限界轮廓上的A，B两点间的线段AB的斜率为正值，即k＞ 0。

图1a— 图1i 分别表示货物轮廓C和建筑限界线段AB不同的相对位置。图1d、图1g 中货物轮廓和建筑限界线段的位置关系满足0 ≤k1≤k且yA≤yC≤yB且xA≤xC条件，不需要计算安全距离，直接判定为不能通过，其他情况需计算安全距离再进行判断[10]。

（2）限界轮廓线段的k= 0 或k＜0 或k不存在时，满足以下3 个条件其中之一，可直接判定为货物不能通过，否则需计算安全距离再进行判断。①0 ≤k2≤k且yA≤yC≤yB且xB≥xC；②k＜0 且(k2≥ 0或k2≤k) 且yA≤yC≤yB且xA≥xC；③k=k1= 0 且xC≤xB。

同理，货物轮廓与建筑限界上的点也存在图1 所示的位置关系，通过分析可以得到结论如下。满足如下4 个条件其中之一，可直接判定为货物不能通过，否则需计算安全距离再进行判断。①xA≤xC且k1= 0 ；②(k＞ 0 或k= ∞) 且0 ≤k1≤k且yA≤yC≤yB且xA≤xC； ③k＜ 0 且(k1≥ 0 或k1≤k) 且yA≤yC≤yB且xB≤xC；④k=k1= 0 且xA≤xC。

限界安全距离的具体计算方法是以点到直线段的最短距离为基准，结合垂足是否在直线段上，计算安全距离。安全距离计算示意图如图2 所示。在图2中，由C点向直线段AB做垂线，当垂足M在线段AB内时，取C点到直线段AB的距离CM作为安全距离。当垂足M在线段AB外时，在C点到A点距离CA和C点到B点的距离CB中选择较短的作为安全距离。

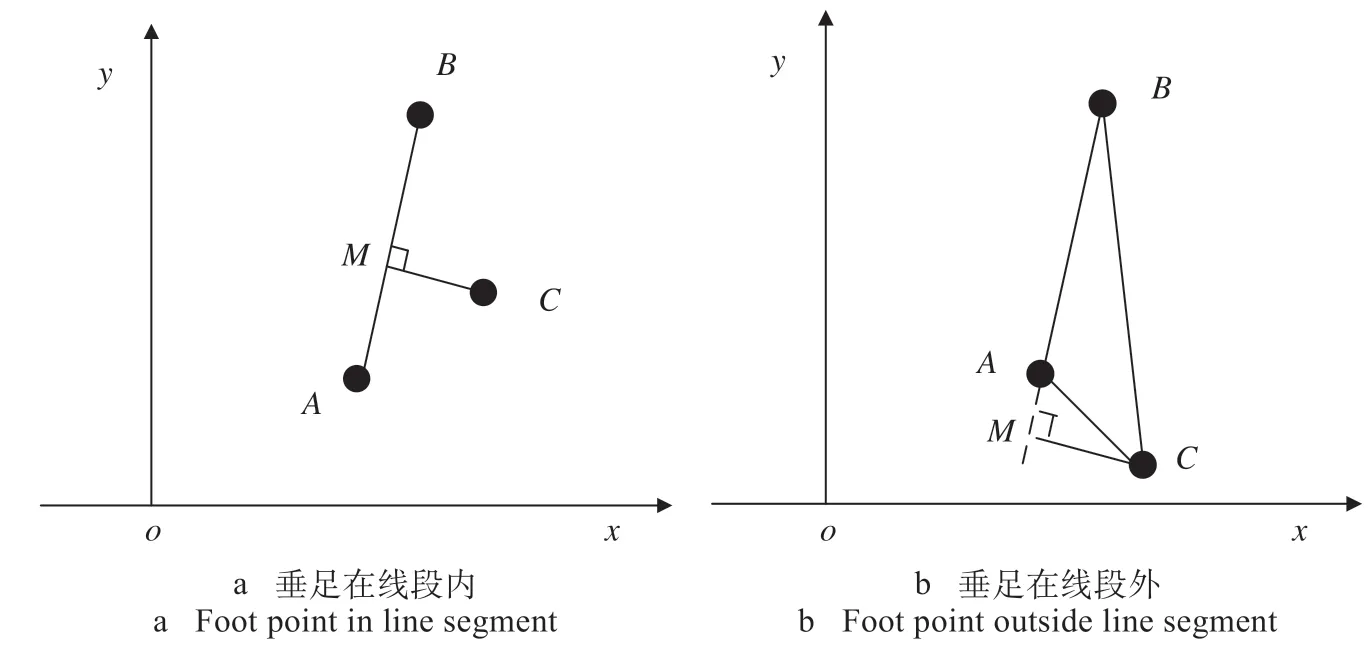
图2 安全距离计算示意图Fig.2 Schematic diagram of safety distance calculation

2.2 安全检算算法设计

限界安全检算算法采用双循环结构，即分别由建筑限界、货物轮廓上的点向货物轮廓、建筑限界做垂线，采用点到直线段最短距离来确定其安全距离。限界安全检算示意图如图3 所示。其中：外侧是建筑限界轮廓(ABCEDFGHIJKL)，内侧为货物轮廓(mnpqrt)。

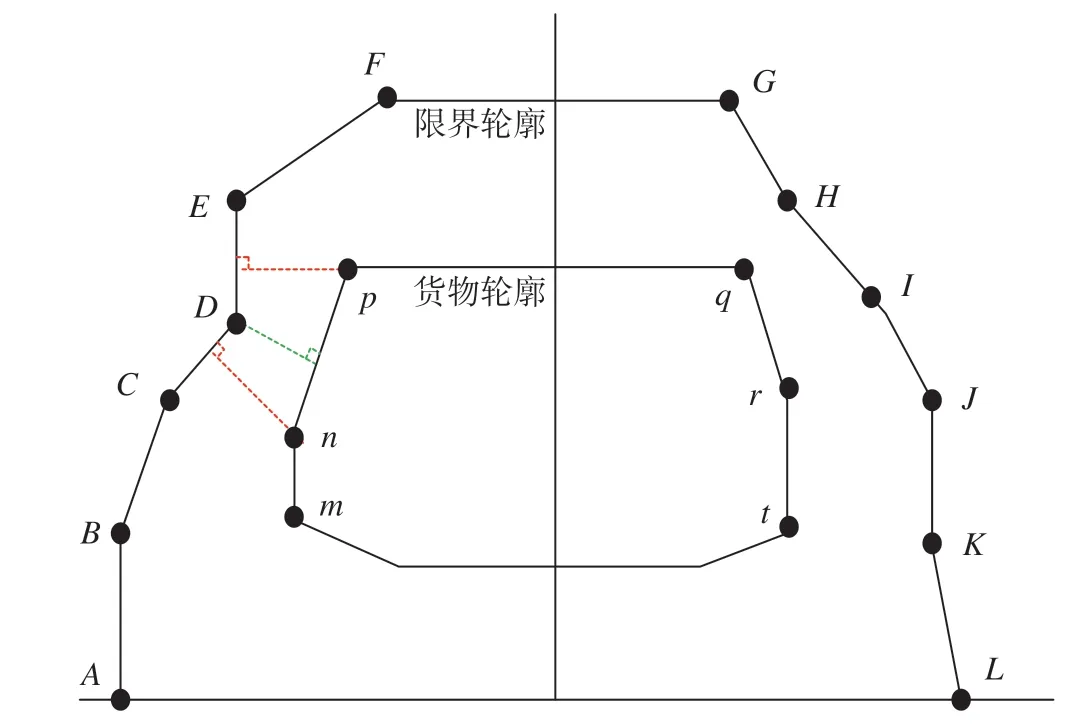
图3 限界安全检算示意图Fig.3 Schematic diagram of clearance safety check

安全检算算法如下。

（1）以货物上突变点为基点遍历限界上的线段：将货物轮廓上突变点( 输入的侧高及对应侧宽) 与限界G轮廓上相应范围内线段逐一进行比对，当满足结论一中任何一条时，判定为不能通过，否则求安全距离t，如果t小于给定距离d，把t和t相关的数据存入A集合。

（2）以限界上突变点为基点遍历货物上的线段：将限界G轮廓上突变点与货物轮廓上相应范围内线段的距离逐一进行比对，当满足结论二中任何一条时，判定为不能通过，否则求安全距离t，如果t小于给定距离d，把t和t相关的数据存入B集合。

（3）令C=A∪B，其中，C为货物与限界G的在给定距离d条件下的信息集合。

3 案例分析

3.1 限界安全检算与传统方法的比较分析

当人工进行安全检算时，一般采用的是建筑限界轮廓和货物轮廓同高程的数据进行比对的方法。同高程比对方法存在安全隐患。举例说明如下。

（1）限界在货物轮廓之外示意图如图4 所示。图4 中A点为货物轮廓上的点，B，C为建筑限界轮廓上的点，AM与直线段BC垂直，M为垂足。采用同高程数据比对时，A，B之间的距离很大，货物被判定为安全通过，且不需要限速。如果采用限界安全检算算法，安全距离为AM，此时A，M之间的距离很小，判定结果要么是不能通过，要么限速通过。经证明，后者更有利于保障安全。

（2）限界在货物轮廓之内的示意图如图5 所示。图5 中A，B为货物轮廓上的点，C，D，E，F为建筑限界轮廓上的点，采用同高程数据比较时，A点与建筑限界EF和B点与建筑限界CD之间的距离很大，货物被判定为安全通过，且不需要限速。如采用2.2 中的检算算法，E点是建筑限界上的点，位于货物轮廓AB左侧，判定结果是不能通过。证明后者更有利于保障安全。

图4 限界在货物轮廓之外示意图Fig.4 Schematic diagram of clearance beyond the outline of goods

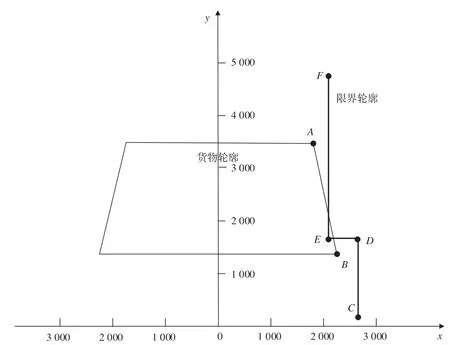
图5 限界在货物轮廓之内示意图Fig.5 Schematic diagram of clearance within the outline of goods

3.2 车辆运行振动情况下的安全性分析

车辆运行过程中的振动有6 个维度，即上下振动、左右振动和前后振动。从不同维度探讨限界安全检算算法的安全性问题。①当车辆左右振动时，货物随着车辆左右晃动。这种情况可以通过预留安全余量的方法来保证安全。利用计算所得的安全距离减去一定的安全余量后，再进行决策， 从而保证安全。 安全余量的设置与车辆的振动情况有关， 车辆上部振动大于下部， 日常工作中预留的安全余量一般为20 ～ 30 mm。关于安全余量预留问题，可以通过实验数据进行统计分析，进而得到更为准确的数值。 ②当车辆上下振动时，货物随着车辆上下振动。这种情况可以在计算货物轮廓时适当扩大货物尺寸来保证安全。在计算货物轮廓时，考虑到货物装车后，车体弹簧的形变，将货物的计算宽度的最大值向下延伸50 mm，这样不但解决了车底板因弹簧形变降低的问题，同时也解决了车辆上下振动的问题，保证了安全。③当车辆前后振动时，对安全性无影响。

4 结束语

限界安全检算是一个相对复杂的过程，涉及到建筑限界、货物轮廓、长大货物车导向决策、径路信息和限界安全距离等方面因素，任何一个环节出现问题都会导致决策不准确，给超限货物的安全运输带来隐患。采用基于等价销距的限界安全检算算法，不但可以避免漏掉建筑限界关键控制点信息，而且计算得出的安全距离准确可靠，有利于保障铁路超限货物运输安全。该算法已在中国铁路南宁局集团有限公司的铁路限界管理及超限超重货物运输辅助决策系统中进行应用，并取得了良好的应用效果。