基于大弹簧的介质侧机械密封腔流场数值分析

，

(南京工业大学 机械与动力工程学院， 江苏 南京 211800)

机械密封是一种用于流体机械或者动力机械中保证设备运行可靠的零部件。其工作原理是通过动环与静环之间相对高速的旋转产生一层薄液膜，这层极薄的液膜将密封介质与缓冲液，或者将缓冲液与大气隔离开，从而达到密封的效果。机械密封工作可靠、适用范围广，炼油装置中85%以上的机泵使用了机械密封[1]。

随着泵内介质变得复杂，对于泵机械密封的要求也越来越高。文献[2-4]通过对机械密封失效分析发现，机械密封产生泄漏的主要原因中包括：①机械密封工作期间有固体颗粒物质进入到密封摩擦端面，导致摩擦端面过早磨损。 ②波纹管和小弹簧因为介质颗粒的聚合失去弹性，无法补偿轴向的位移。对于介质中含有固体颗粒的机械密封，通常采用适当的冲洗方案来减少固体颗粒或污染物[5]。目前国内常采用API 682—2012《Pumps-shaft Sealing System for Centrifugal and Rotary Pumps(4th Edition)》[6]中的冲洗方案[7]。API 682—2012中的冲洗方案需要在机械密封外部设置额外的循环管路，在某些不允许改变外部循环管路的工况下，可选择在机械密封内部增加流动改变装置来改善密封端面的工作状况。

目前关于机械密封腔内的数值研究主要集中于温度场、压力场和速度场[8]。任立朝等[9]利用计算流体动力学对复杂工况下机械密封腔内流场进行数值模拟，研究了冲洗口位置对密封腔内流场的影响，并得到了最佳冷却位置。张明明等[10]的模拟研究结果显示，适当增加冲洗液的流量可以降低密封端面的温度，而且密封端面温度随介质压力或旋转速度的增大而升高。目前对于密封腔内含有固体颗粒的固-液两相流的研究相对较少。Azibert等[11]运用FLUENT软件模拟了不同工况条件下机械密封腔内固体颗粒的分布情况，设计了一种锥形的旋转结构，减少了固体颗粒在密封端面的分布。

文中运用FLUENT软件对机械密封介质侧密封腔内固-液两相流场进行数值模拟，分析弹簧和泵送环对密封端面处颗粒流动速度的影响以及颗粒体积分数的分布状态。

1 控制方程

流体动力学的基本控制方程包括质量守恒方程、动量守恒方程和能量守恒方程[12]。连续性方程即质量守恒方程，按照质量守恒定律，单位时间内流出控制体的质量应该等于同样时间内控制体内减少的质量，由此可推导出流体流动连续性方程的微分形式为：

(1)

式中，ux、uy、uz分别为x、y、z这3个方向的速度分量，m/s；t为时间，s；ρ为密度，kg/m3。

动量方程可描述为，对于一给定的流体微元体，其动量对时间的变化率等于外界作用在该微元体上的各种力之和。根据这一定律，可导出x、y、z这3个方向上的动量方程为：

(2)

(3)

(4)

式中，p为流体微元体上的压强，τxx、τyx、τzx、τxy、τyy、τzy、τxz、τyz、τzz分别为因分子黏性作用产生的作用在微元体表面上的黏性应力τ的分量，Pa；fx、fy、fz为3个方向的单位质量力，N/kg。

由于不考虑温度的变化，所以控制方程中只包含了连续性方程和动量方程[13]。

2 机械密封腔内流体三维计算模型

2.1 物理模型建立与网格划分

机械密封介质侧密封腔结构示意图见图1，图中动环与静环之间为密封摩擦端面，弹簧可以补偿泵轴轴向窜动的位移量。

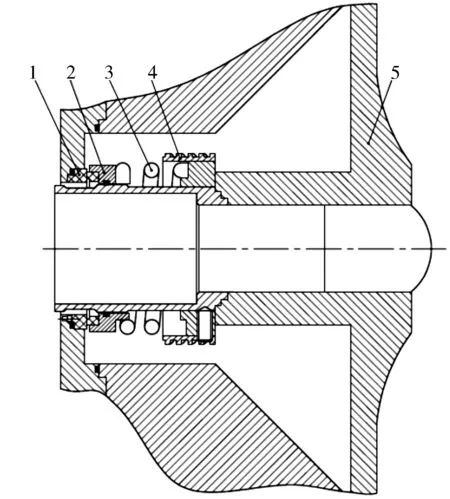
1.静环 2.动环 3.弹簧 4.泵送环 5.叶轮 图1 机械密封介质侧密封腔结构示图

由于研究对象为流体，因此将机械密封腔内流体区域的模型提取出来。为便于观察，将模型沿轴线半剖，得到的几何模型见图2a。流体区域为封闭结构，通过弹簧和泵送环的搅动作用改变颗粒的速度与体积分数。

进行网格划分时，需要对流域中旋转的部件和壁面进行旋转交界面设置。交界面越靠近旋转部件，旋转部件对周围流体区域的影响越小。交界面越靠近壁面，旋转部件对周围流体区域的影响越大。因此将交界面位置选择在壁面与旋转部件之间，靠近旋转部件的1/4处[14]。由于模型较为复杂，故采用非结构网格进行划分，划分网格数1 444 778，节点数267 169(图2b)。

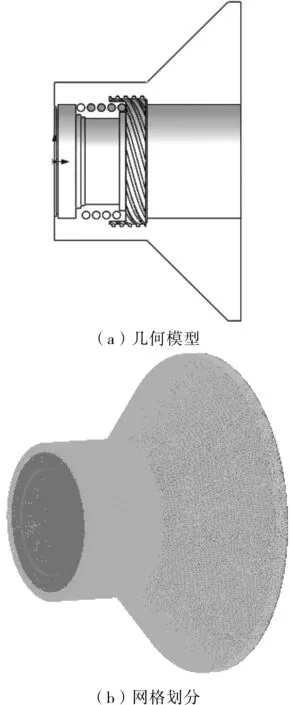
图2 机械密封腔内流体区域几何模型及网格划分

2.2 数值计算模型和求解方法选择

机械密封腔内液体与固体颗粒的流动属于多相流，欧拉模型计算结果精度相对较高[15]，故选择欧拉模型为数值计算模型。旋转作用下机械密封腔内的流动较为复杂，在计算时作如下假设：①将液相介质视为不可压缩流体，且每一相的物理特性为常数，不发生改变。②视固相颗粒为球形，不考虑相变。③液相和固相皆为物性不变的连续相。

模拟时，泵轴的转速不发生改变。机械密封腔内的流动属于定常流动，选择标准k-ε湍流模型和SIMPLE算法进行定常数值计算，使用Phase Coupled SIMPLE 算法求解压力-速度耦合方程组。

2.3 边界条件设置

机械密封腔内流场数值模拟的边界条件包括泵送环壁面、弹簧壁面、轴套和叶轮的壁面以及密封腔体的内壁面。其中泵送环壁面和弹簧壁面与交界面形成1个圆柱形的转动区域，而其他区域则为静止区域。这样在动静区域之间存在一组动静耦合的交界面，2个区域通过交界面进行数据交换，可以通过多重参考系法(MRF)来描述。

将轴套壁面和叶轮壁面设置为运动边界，将密封腔体的内壁面设置为静止边界。对于所有的壁面，均采用无滑移壁面边界条件[16-18]。

2.4 介质物性

液体介质为精丙烯酸，其密度为1 050 kg/m3，黏度为0.001 149 Pa·s。

固体颗粒选用的是丙烯酸树脂，其颗粒密度为2 170 kg/m3，颗粒直径为0.05 mm。

3 机械密封腔内三维流场模拟结果与分析

将模型导入FLUENT软件，设置泵轴转速为1 500 r/min，重力加速度为9.8 m/s2，方向为y轴的负方向。机械密封腔内的介质为液相丙烯酸和固相丙烯酸树脂颗粒的混合物，设置丙烯酸树脂颗粒的体积分数为10%。分别在无弹簧和泵送环、有弹簧无泵送环及有弹簧和泵送环这3种条件下对机械密封腔内三维流场进行数值模拟。由于模型较为复杂，为了便于观察，分别取密封端面所在平面和与轴线平行的平面位置进行结果分析。

3.1 固体颗粒流场

不同条件下机械密封腔内固体颗粒流线分布见图3。从图3a可以看出，在叶轮旋转作用下，靠近叶轮侧的机械密封腔体内形成1个较大的环流，而其他位置的颗粒都围绕在密封端面附近流动，颗粒容易聚集在密封端面附近。从图3b可以看出，机械密封腔内颗粒的流线形成3个环流，最左侧靠近密封端面处形成1个较小的环流，在该环流的作用下，密封端面处的颗粒可以沿着该环流循环流动，从而减少颗粒在此处的聚集。中间位置处的环流主要是由弹簧的旋转产生的，并且该环流能够带走部分左侧小环流内的颗粒。右侧最大的环流则是由叶轮的旋转产生的，由于叶轮的径向尺寸较大，所以在叶轮边缘位置颗粒的速度最大，达到了19.6 m/s。从图3c可以看出，左侧密封端面处没有形成环形流域，且在泵送环的影响下，中间的环流范围较图3b中的环流范围大。在增加了泵送环后，颗粒不容易在密封端面处堆积且更容易流向叶轮侧的机械密封腔内部。

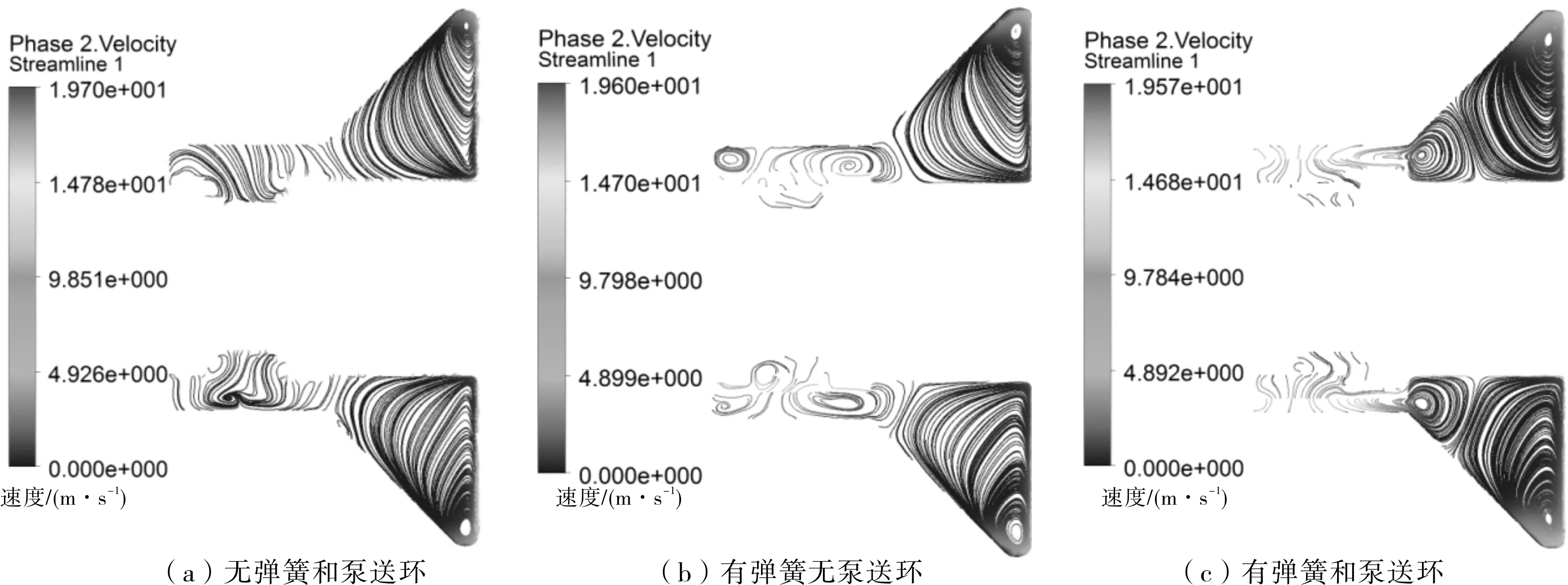
图3 不同条件下机械密封腔内固体颗粒流线分布

3.2 固体颗粒速度

3.2.1分布云图

在3种不同条件下机械密封腔内固体颗粒轴向速度场分布云图见图4。在速度场中，正值代表流速方向为x轴的正方向，负值代表流速方向为x轴的负方向。

对比图4a和图4b可以发现，弹簧的旋转对流体有一定的推动作用，且最大速度出现在弹簧座与壁面的间隙处，此处径向尺寸减小所以流速增加。图4c中最大流速出现在泵送环的齿形间隙内，且该位置处颗粒的轴向速度高于图4b中颗粒的轴向速度。

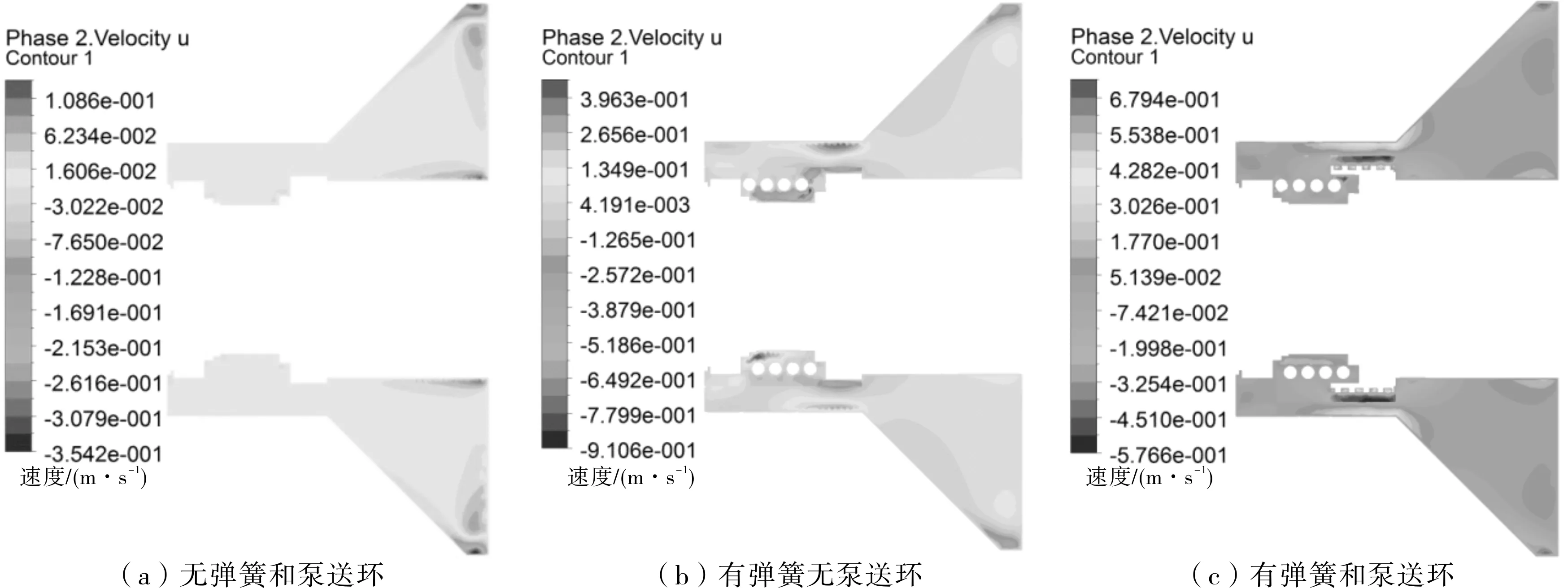
图4 不同条件下机械密封腔内固体颗粒轴向速度场分布云图

3.2.2变化曲线

不同条件下机械密封密封端面所处平面流场在x=0.001 5 m、z=0 m且y从0.041 5 m变化到0.062 5 m直线上的颗粒速度变化曲线见图5，机械密封轴向平面流场在y=0.055 m、z=0 m且x从0 m变化到0.146 m直线上的颗粒轴向速度变化曲线见图6。

从图5和图6可以看出，在无弹簧和泵送环的条件下，颗粒的速度基本在0.01 m/s左右，由于没有弹簧和其他旋转零件的影响，颗粒的速度很低且变化很小。增加了弹簧之后，颗粒的速度明显提升。在密封端面处颗粒的轴向速度最高达0.03 m/s、径向速度最高为0.04 m/s。在有泵送环的流场中，其密封端面上颗粒轴向速度最大值达到0.08 m/s，相较于没有泵送环的最大流速增加了0.05 m/s。在其他位置处，有泵送环时颗粒的速度基本都大于没有泵送环时颗粒的速度。有泵送环时颗粒的径向速度最大值为0.11 m/s，比无泵送环时同一点处的速度增加0.07 m/s。轴向平面上泵送环产生的影响更明显，泵送环使颗粒的最高速度达到0.55 m/s，而没有泵送环时颗粒的最高速度为0.2 m/s。在有泵送环和无泵送环条件下，颗粒速度的最高值出现在0.05～0.075 m这段距离，该段处于泵送环与密封腔体内壁面之间，由于此处间隙相对较小，且泵送环对流体具有推动作用，故颗粒速度在此处达到最大值。当轴向距离远离泵送环时，泵送环对颗粒的作用逐渐减小，颗粒的轴向速度也随之降低并最终趋于0。

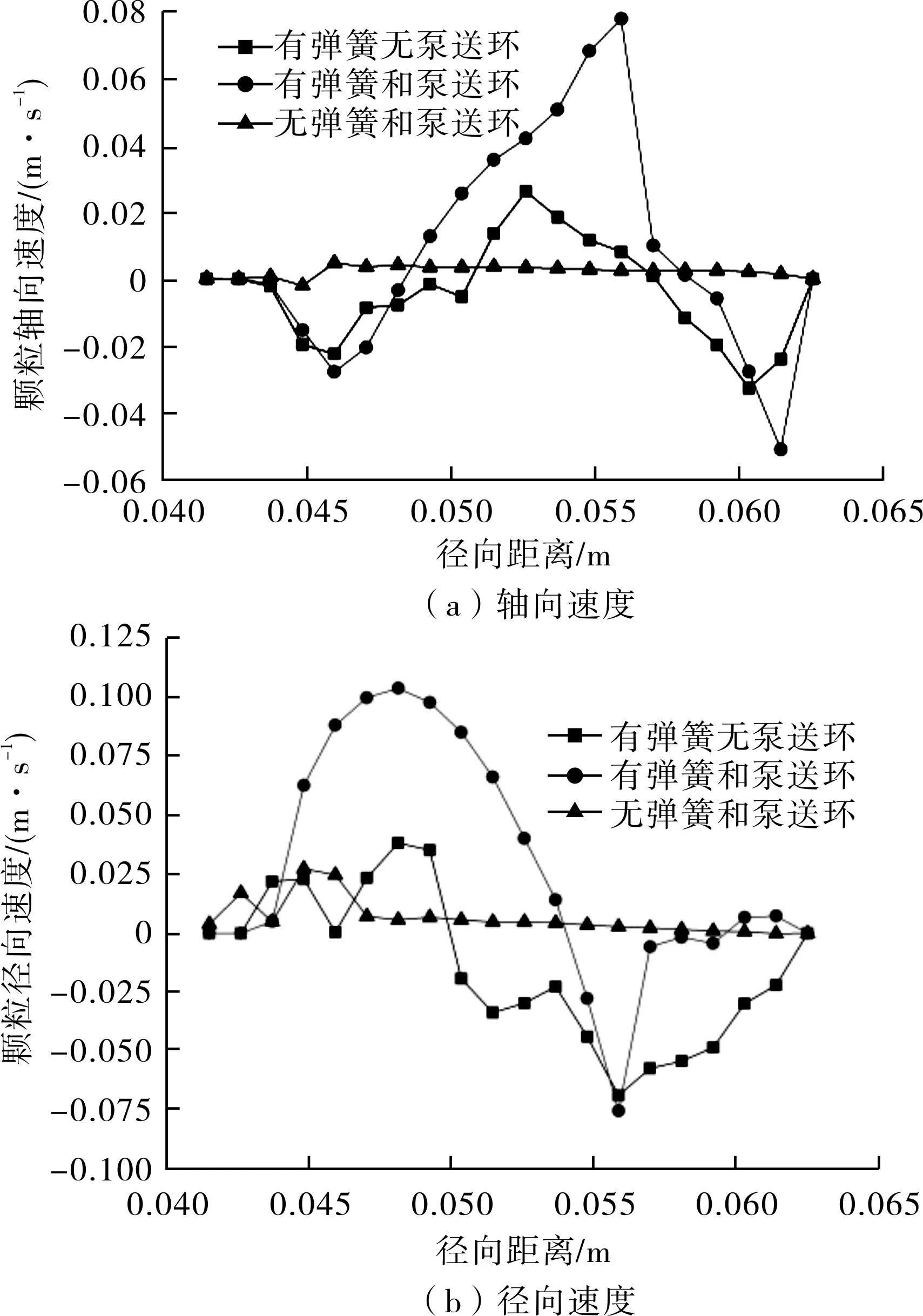
图5 不同条件下机械密封密封端面所在平面颗粒速度变化曲线

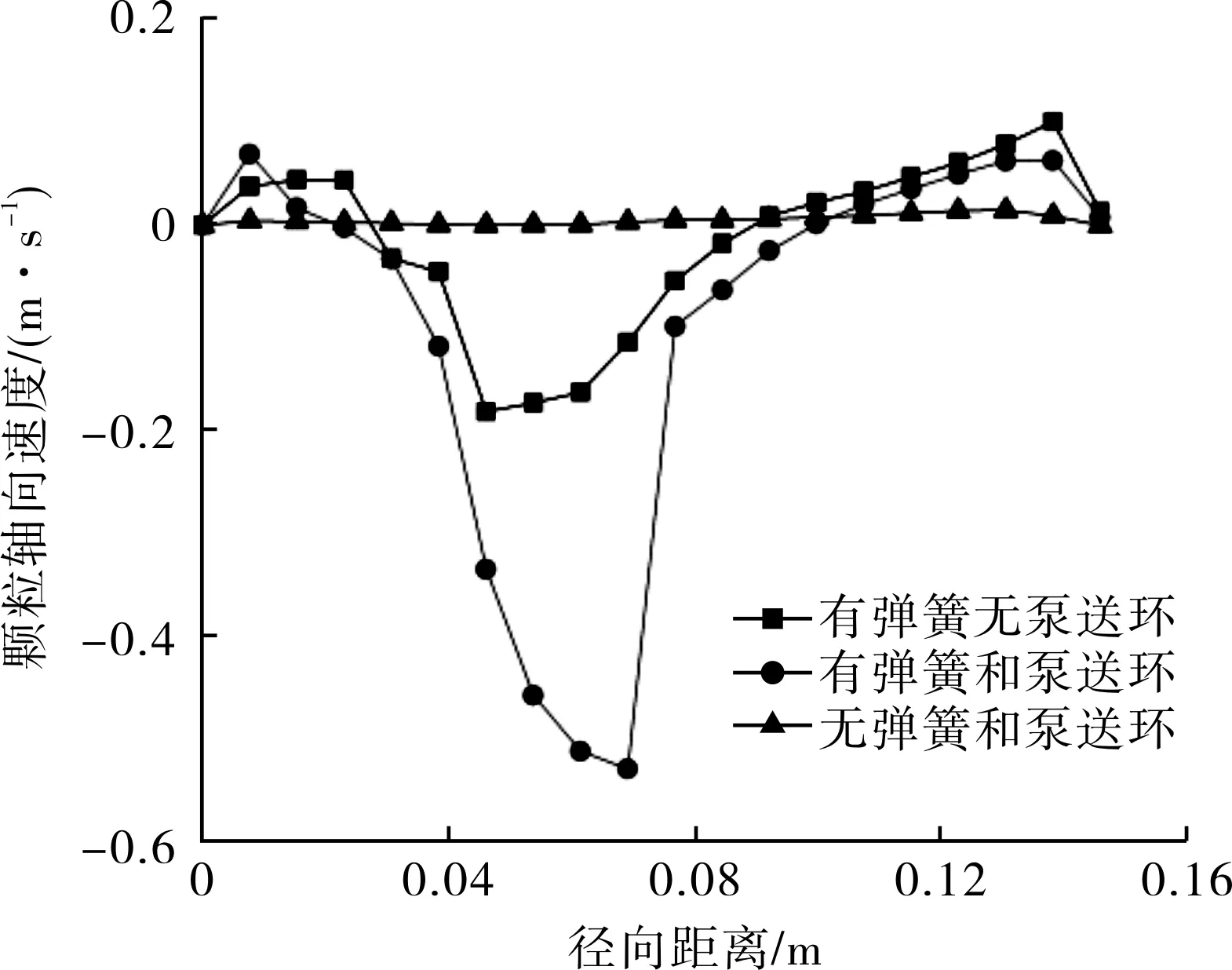
图6 不同条件下机械密封轴向平面颗粒轴向速度变化曲线

3.3 固体颗粒体积分数

3.3.1分布云图

不同条件下机械密封轴向平面颗粒体积分数分布云图见图7。

从图7a可以看出，由于没有弹簧和泵送环的旋转搅动作用且受自身重力的影响，颗粒最终聚集在密封腔的底部。从图7b可以看出，密封腔内的颗粒体积分数在0.1左右。弹簧在自身的旋转作用下产生一定的搅动作用，弹簧中间段颗粒的体积分数减小到约0.03。在下方的锥形壁面上，由于弹簧对流体的推动作用不够大，同时在重力作用下，颗粒体积分数会有所升高。结合前述对颗粒速度的分析可知，在泵送环的作用下，密封腔内的液体被泵送环推送至密封端面附近，对密封端面形成一定的冲洗效果，且在冲洗过程中可以带走弹簧两端的颗粒，使弹簧所处位置的颗粒体积分数进一步减小(图7c)。

图7 不同条件下机械密封轴向平面颗粒体积分数分布云图

不同条件下机械密封密封端面所在平面颗粒体积分数分布云图见图8。泵轴及轴上的旋转件在高速旋转的过程中会产生一定的离心力，减少颗粒物质在密封端面上的附着。比较图8b和图8c可以发现，在离心力作用下，颗粒体积分数随密封腔径向尺寸的增大而增大，在泵送环影响下，该现象更明显。

图8 不同条件下机械密封密封端面所在平面颗粒体积分数分布云图

3.3.2变化曲线

不同条件下机械密封密封端面所在平面在x=0.001 5 m、z=0 m，并且y从0.041 5 m变化到0.062 5 m直线上的颗粒体积分数变化曲线见图9。在无弹簧和泵送环条件下，颗粒的体积分数变化趋势明显不同于其他2种情况，其颗粒体积分数呈逐渐减小的趋势，在最靠近密封端面处，体积分数达到0.09，为3种条件中的最高值。在有弹簧的条件下，颗粒体积分数随着径向尺寸的增大而逐渐增大。对于没有泵送环的情况，靠近密封端面处颗粒的体积分数为0.05，壁面处颗粒的体积分数约0.13。结合前述对颗粒速度分析的结果可知，增加泵送环后，泵送环提高了颗粒的径向速度，使颗粒在密封端面处的体积分数趋于0，且在y=0.041 5 m至y=0.055 m这段距离内，颗粒体积分数一直小于没有泵送环的情况。随着径向尺寸的增加，颗粒体积分数逐渐升高到0.2左右。

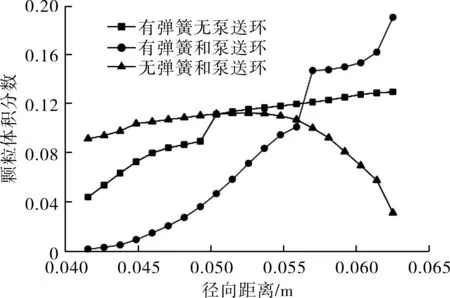
图9 不同条件下机械密封密封端面颗粒体积分数变化曲线

不同条件下机械密封轴向平面在y=0.055 m、z=0，x从0变化到0.146 m直线上的颗粒体积分数变化曲线见图10。从图10可以看出，在该直线上，有泵送环情况下的颗粒体积分数基本高于没有泵送环的情况。在泵送环的推动和旋转作用下，固体颗粒更多分布在靠近壁面的位置以及右侧的腔体内。在无弹簧和泵送环条件下，颗粒的体积分数最小。在有弹簧和泵送环条件下，颗粒体积分数介于其他2种情况之间。这种现象说明弹簧及泵送环旋转产生的离心力使颗粒围绕密封腔的内壁面均匀分布，且密封端面处颗粒的体积分数在离心力和搅动作用下明显减小。

图10 不同条件下机械密封轴向平面颗粒体积分数分布曲线

4 结语

运用多重参考系法和欧拉模型对机械密封腔内流场进行了三维数值模拟，模拟结果显示，在无弹簧和泵送环的条件下，密封腔内的颗粒主要受重力的影响，容易附着在密封端面处以及密封腔的底部。增加弹簧后，弹簧旋转对流体产生一定的推动作用，密封端面的颗粒明显减少，且颗粒的轴向和径向速度增加，有利于阻止颗粒进入密封端面，从而减少密封端面的磨损。增加泵送环后，密封端面处的颗粒体积分数进一步降低，固体颗粒在弹簧和泵送环旋转及推动作用下向壁面处和右侧腔体靠近。

在机械密封的设计和改进中，需要充分考虑密封摩擦副端面附近颗粒的流动状态和分布情况，可以通过增加额外的流动改变装置来减小密封端面附近颗粒的体积分数。