初中数学解题教学中学生审题能力培养探讨

莫海东

【摘要】审题环节出现错误，是学生解题错误的主要来源之一。文章结合多年一线初中数学教学实践经验，从审题先粗后精，强化信息梳理，把握隐藏条件三大方面，对在初中数学解题教学中如何培养学生的审题能力进行了分析探讨。

【关键词】初中数学解题教学;审题能力;学生

解题是数学学习活动中最基础的活动之一。大数学家波利亚将“理解题意”作为数学解题四部曲中的第一步，而“理解题意”也即我们常说的审题环节。审题环节出现错误，会直接导致所获取的有效信息不全或失真，从而在解题中陷入歧途，这也是学生解题错误的主要来源之一。因此，如何在初中数学解题教学中更有效地帮助学生在熟悉题目的基础上，进一步深入挖掘、分析题目中包括隐含条件在内的已知条件的深层次有效信息并正确地加以充分应用，从而寻找到正确解题的金钥匙，是提高学生数学能力、增强数学解题训练有效性的关键因素之一。现笔者结合多年一线初中数学教学实践经验，就该问题进行分析探讨。

一、审题先粗后精，抓住关键有效信息

众所周知，数学题目的构成要素主要为“条件”加“问题”，实践中学生面对各种条件错综复杂的题型，只有第一时间“快、准、深”地获取有效信息，才能迅速解题[1]。然从笔者多年的教学实践来看，很多学生在解题过程中往往在审题第一步即出现各种问题，概括起来比较常见的主要有忽视范围，忽视条件，不能分辨近似题题意，梳理信息时出现错误，曲解题意等等，最终导致解题进入误区。

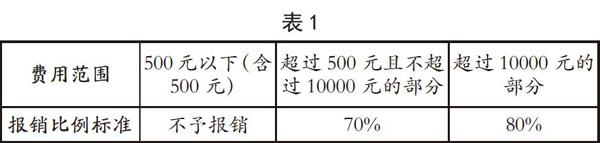
例1：我国农村纳入医疗保险的农民医疗费的报销比例如表1。

从学生解题情况看，第一个问题基本上没有太大错误，而第二个问题答错率较高，学生错误作答如下。

，分两种情况：①，x-70%x =3500，，不成立;②10000，x-80%x=3500，，该农民当年实际医疗费为17500元。

学生之所以出现答题错误，关键在于审题时粗心大意，没有注意到“500以下不予报销”这一条件，只是片面地考虑“超过500且不超过10000元的部分”此一信息条件便匆忙进行答题，从而最终造成答案错误。

因此，面对各种条件错综复杂的题型，为最大限度地避免出现如上错误，教师应引导学生在审题环节带着问题入手，先粗读问题，再看条件，认真分析该题目的条件和结论是什么，与哪些己知的数学知识有关，再进一步进行精读，深入把握解题所需的己知量、未知量和条件等关键有效信息，以便快速地找到问题破解的关键信息。此外，一些题目中会存在一些干扰项，很多内容实际与解题没有丝毫关系，这就是我们常说的“无效信息”。因此，在审题时还要注意引导学生学会取实去虚，在精读时有针对性地排除掉这部分无效信息，从而切实提高审题效率。

二、强化信息梳理，提升分析问题能力

数学知识抽象繁杂，各类型题目中往往包含众多的数据或条件。鉴于学生在数学知识储备及数学思辨能力上的不足，在审题时凭借一眼便能迅速从众多数据之间发现有效数据或理清各数据（条件）之间存在的联系的想法并不现实，也不可能，因而教师在实践教学中应尽可能地提高学生对题目中信息的梳理能力，以便在解题时更好地在已知条件（量）和未知条件（量）之间建立关系，最终达到提升学生分析问题和解决问题能力的目的[2]。

例2：如图1，边长为的等边中，点是高所在直線上的一个动点，连结，将线段绕点逆时针旋转得到，连结，则在点的运动过程中，线段长度的最小值是（    ）：

A.;B.;C.;D.

在审题时，笔者先让学生试着对题目中的众多信息进行梳理，很快便有学生找出了题目中的关键有效信息——“将线段绕点逆时针旋转”。通过此信息，我们很容易便可得出题目中隐藏的关键条件——△为等边三角形，再结合题中已有的等边△，这一题目的实质已经清楚明了：该题目为一个“双等边三角形”的常见数学模型。

在此基础上，笔者再引导学生回忆以往积累的一线三等角模型、“K”型相似模型、“中点+平行”模型、双等边角形模型、双等腰直角三角形模型等各种基本数学模型，然后让学生讨论解题时需要运用到的模型知识。学生很快得出如下解题思路。

如图2，连接，△为等边三角形，BC，。 绕点逆时针旋转 得到CN，，，，即，，。为等边△的高线，BH=CH=a，。点N在所在直线上运动，作于点，则即为的最小值，，，。

三、把握隐藏条件，抓住问题本质提升能力

初中数学题型千姿百态变化万千，实践中，学生经常会遇到一些貌似“条件不足”的题目，从而最终导致解题无从下手。究其原因，其实并非题目所给条件不足，而是学生在审题时不能对题目做到深入挖掘，从而也就难以获取题目背后所蕴含的深层条件，最终导致解题效率大打折扣[3]。

例3：如图3，P为正三角形外接圆的劣弧上任意一点（不与、重合），求证：。

该题目就是比较典型的“条件不足”题型，学生在解题时如果单纯地依据题目表面上所给的已知条件，则往往会陷入“好像条件不足”的桎梏。针对此类问题，教师在审题环节要加强引导学生认真观察图形，通过对以往知识的回忆、归纳，找出题目中隐藏的相关定理为己所用。

此题中学生对图形进行观察后很容易发现为圆内接四边形，根据所学习的托勒密定理可知，又△为正三角形，，从而得到本题求证：。

实践中，类似在解题过程中需要运用某定理但题中条件并未提及的情况较为普遍。因此，将题目中所给出的已知条件看全、看透，是不容忽视的一个重要环节。要做到这一点，认真观察、寻找问题的本质是关键。这就要求学生在审题过程中要关注到题目中的每一个细节，将叙述的问题把握完整，方能有效实现高质量解题。

总之，要想有效提升学生的数学水平，不能只注重学生的做题能力，审题能力同样至关重要。实践中，学生审题能力参差不齐的现象在当前的初中数学教学中依然比较普遍。因此，采用各种切实有效的手段，帮助学生掌握一定的解题思维策略，从而有效培养学生的数学审题能力，是所有数学工作者应关注的重点课题。实践中，除加强相关研究，采取针对性措施以外，还应做好从一般到抽象的归纳总结[4]：做好各类题型的分类，把相同题型进行统一划分，以方便后期的总结;做好各类题型的对比，分析各类题型的题干、问题的特点及其中的异同，以便下次遇到类似问题时能最快地找出解题密码;勤于总结，尤其是对于常见的审题错误情况更要加强总结，从错误资源中找出问题的根本所在，从而最大限度地减少学生下次再犯类似错误的可能。如此，不断进行审题策略的完善和改良，最终达到切实提高数学教学实效性的目的。

【参考文献】

[1]李燕.提升学生审题能力的三类策略[J].初中数学教与学，2014（17）：11-12.

[2]石毕玉.多角度审题，多维度升华[J].初中数学教与学，2018（10）：38-41.

[3]张佶迪.关于提升初中学生圆问题审题能力的实践研究[D].长沙：湖南师范大学，2017.

[4]姚小妹.初中数学解题教学中学生审题能力的培养[J].教育现代化，2018（31）：55-56.