基于区域生长算法的土石混合介质细观识别与数值模拟研究

戴 薇 石 崇 阮怀宁 孔 洋 杨俊雄

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室， 南京 210098； 2. 河海大学 岩土工程科学研究所，南京 210098)

土石混合介质[1-2]是指第四纪以来形成的，由具有一定工程尺度、强度较高的块石、细粒土体及孔隙构成且具有一定含石量的极端不均匀松散岩土介质系统，是一种由作为骨料的石块与作为充填料的土组成的地质体．由于两种组分在强度、变形特征等方面的差异，使得土石混合介质表现出典型的非均质性、非线性性以及非连续性，同时，在自然界中，不同场地下土石混合介质分布情况各不相同，甚至有很大差别，故基于图像数字识别技术建立土石混合介质的数值模型，对于分析不同土石混合介质的特性，具有更加普遍的意义．

目前对土石混合介质的研究主要分为现场试验和数值模拟两方面．徐文杰等[3]对虎跳峡龙蟠右岸土石混合介质分别进行了天然状态下和浸水条件下的原位大型推剪试验，获得了土石混合体强度参数的参考值并证明土石混合介质的强度与含石量有关．胡峰[4]等考虑不同含石量、不同上覆压力、不同块石尺寸进行剪切变形试验，揭示了土石混合体滑坡剪切带形成演化规律、破坏模式．但由于现场试验受到场地以及试验条件的约束，数值试验成为更令人青睐的研究方式，廖秋林等[5]基于基于块石与土体的颜色属性差异识别土石混合介质，并通过有限元方法研究了土石混合介质的力学特性．徐文杰等[6]通过数字图像方法及大型直剪试验分析了块石含量与抗剪强度的关系．丁秀丽等[7]对土石混合介质进行灰度处理和边界重构，进而建立了土石混合介质的颗粒流模型，并对模型进行了双轴压缩试验．金磊[8]等通过CT扫描不规则颗粒生成三维离散元模型，进行大三轴试验数值模拟研究．

目前对于土石混合介质的研究多基于随机重构，不能反映现场的实际土石分布状况，另外，基于数字图像分析方法建立研究模型，可以避免由于室内试验采样所造成的土样扰动等影响，可以较真实再现原位试验下土石混合介质的力学特性．对于现场拍摄的数码照片，在预处理的基础上采用区域生长算法进行数字图像识别，实现土石混合介质的二值化．在此基础上生成土石混合介质的数值模型，进行数值试验，进一步研究其强度特性及颗粒间的接触关系．

1 数字图像原理

在计算机中，数字图像[9-10]是由一个个的像素点构成的，像素点的值记录该像素点的色彩、亮度和对比度等图像信息．因此可以根据像素点的信息了解整个图像的信息，这些像素点对应的各个离散数据便成了数字图像处理的基础．

将一副数字图像看作由N×M的像素点组成的矩阵，每个像素点的灰度值对应到其所在的坐标，以二维函数f(i，j)表示，其中i，j为空间坐标．

(1)

式中，N与M分别为图像中水平与垂直方向的像素数量．

2 数字图像识别过程

2.1 图像预处理

如图1(a)所示，将现场拍摄的彩色图像进行灰度化，分析其特征线上的灰度分布曲线．如图1(b)所示，原始图像中由于受光照条件、土石混合介质内部矿物质色彩差异等因素的影响，存在大量噪声，难以选取适当的识别准则将内部的土石区分．因此，必须对原始图像进行适当的预处理，增大土石混合介质内部土和石块的差异，便于土石阈值的选取．

图1 土石混合介质灰度图像及其特征线的灰度分布曲线

将原始图像首先经过中值滤波[11]，去除图像中的椒盐噪声，再通过聚类方法[12-13]将像素点进行分类，将图像中的目标区域和背景区域互不重叠的区分开来，最后适当调节图像的对比度，使土石差异更加明显，预处理后图像如图2(a)所示．

2.2 土石阈值的确定

在土石混合介质图像识别中，需要确定一个土石阈值来区分土和石块，阈值T的选择很重要，它是区分土石边界的关键问题．阈值确定函数可以写为一般形式：

T=T[x，y，p(x，y)，f(x，y)]

(2)

式中，f(x，y)表示灰度值；p(x，y)为某种图像性质，即阈值T一般是p(x，y)，f(x，y)，(x，y)的函数．图像的灰度直方图可以反映一幅图像中的灰度分布信息，是阈值选取的重要参考依据．如图2(b)可见预处理图片中特征线上的灰度直方图中出现明显的峰段和谷段特征，分别对应图2(a)中的块石和土，以图像特征线的灰度分布直方图为依据，选取区域生长算法中土石介质的阈值．

图2 预处理图像及其特征线的灰度分布

2.3 区域生长算法

土石混合介质是由具有不同特征的土和石块构成的，土和石块有着相似的内部特征，而相邻的土与石块具有不同的特征，即在一个区域内部满足某种特征的一致性，而相邻的不同区域具有不同的特性．区域生长算法[14-16]即基于上述特点的区域分割方法，其基本思想是将某范围内具有某些相似性质的像素合并起来作为一个“区域”，首先需要寻找一个种子点，如将石块的中心点作为区域生长的种子点，根据一定的生长规则，将种子点周围邻域的与种子点具有相同性质的点合并到种子点的区域．然后以新点作为种子点，继续以上生长过程，直到该区域内没有满足要求的点为止．区域生长算法是一种串行区域分割的图像识别方法，其优点是基本思想相对简单，通常能将具有相同特征的联通区域分割出来，并能提供很好的边界信息和分割结果．

设有一个数字图像，以图3(a)中灰度最大值点作为种子，该点的灰度为9．假设采用的生长相似准则为邻点的灰度与已生成的区域的平均灰度的差小于2，第一次区域生长得到3个灰度为8的邻点，如图3(b)所示．此时4个点已接受点的平均灰度(8+8+8+9)/4=8.25，故第二次区域生长只得到灰度为7的一个邻点，如图3(c)．此时，这5个已接受点的平均灰度为(8+8+8+9+7)/5=8，已不存在灰度大于6的邻点，所以生长过程终止．

图3 区域生长法实现过程

在生长过程中，为了识别结果更为准确，采用人工选点方法，作为区域生长的种子点，即生长起点．根据第二节中确定的土石阈值，将区分土石的灰度值设置为160．在生长过程中，首先判断种子点是否为图片边界点，然后判断种子点周围8个点的灰度值，将符合生长规则的点设置为黑场，并且作为下一步生长的起点．最后将所有满足要求的点纳入同一区域，生成土石混合介质二值图像．

土石混合介质原始图像如图4所示，首先利用2.1节的方法对其进行预处理，然后利用区域生长算法进行土石介质识别，识别结果如图5所示．可见，预处理在很大程度解决了数码图像中的噪点、土石边界模糊以及块石内部矿物色彩差异等问题，直接使用区域生长算法对数字图像进行识别，得到的二值图像中已有明显的土石分布特征．最后，对于图中仍存在由于石块边缘处阴影造成的石块周围的孤点、伪点进行局部处理，如图6所示．

图4 原始图像 图5 二值图像

图6 局部处理后的二值图像

3 土石混合介质离散元模型

前文已根据区域生长算法对土石混合介质的原始图像进行了分割处理，在此基础上可建立离散元模型[17-18]，通过离散元方法对土石混合介质在直剪试验下的力学特性进行研究．

3.1 离散元模型的建立

现场拍摄的数字图像是由一个个像素点组成的，若要生成数值模型，还需要确定实际尺寸与像素之间的比例关系，若S为数字图像中每个像素单位所代表的实际尺寸，L为数字图像在横向或纵向的实际尺寸，N为该方向上的像素点个数，则转换比例为S=L/N．现场拍摄的土石混合介质数字图像为0.3 m×0.3 m的正方形图像，其像素尺寸为1 000Pixel×1 000 Pixel，即转换比例为S=L/N=0.000 3 m/Pixel．

为分析土石混合介质的力学效应，基于离散元方法对上述模型进行直剪试验．如图7所示，模型尺寸为0.3 m×0.3 m，像素尺寸1 000 Pixel×1 000 Pixel，像素单元数为1 000 000．在该模型范围内生成孔隙率16%，半径在0.000 5 m到0.001 m之间的颗粒共41 244个．试样直接剪切试验的模拟边界条件与加载条件如图，上下剪切盒的高度均为0.15 m，根据室内直剪试验的规格，在试验过程中保持上剪切盒不动，推动下剪切盒，利用伺服加载机制使其正应力保持不变．建立墙体作为剪切盒的外墙模型，在试验中认为墙体是刚体，即将墙体的刚度设置得远大于土石介质的刚度．当剪切位移达到0.012 m时，终止试验．试验中每组试样法向应力分别取200、400以及800 kPa．

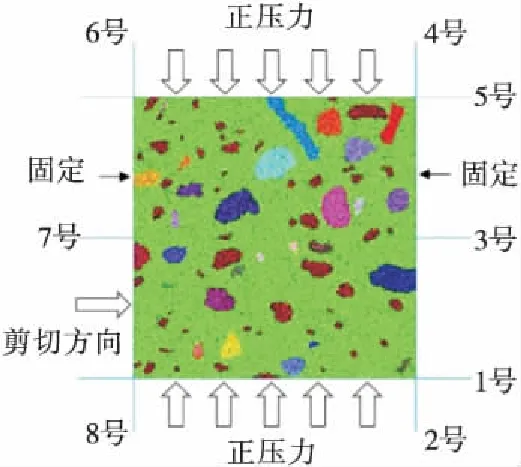
图7 土石混合介质离散元模型

3.2 土石介质细观参数的确定

根据颗粒流方法进行数值模拟首先需要进行细观参数的标定，即探究模型宏观参数与细观参数的关系来确定细观参数．目前对岩石材料宏细观参数关系基本认识如下[19]：1)细观粘结模量控制宏观杨氏模量(E)；2)k*影响弹性变形阶段的泊松比；3)法向与切向粘结强度比影响试样的破坏模式．

首先，采用clump来模拟碎石，在每次循环都不考虑构成clump颗粒之间的相互作用，同时若一个接触中两个颗粒的细观参数不同时，在计算时选取两个参数中最小的一个，但颗粒的接触刚度除外．根据石崇[20]提出的参数标定方法，采用双轴试验对土和石块的细观参数进行标定，最终确定土石混合介质离散元模拟参数见表2．

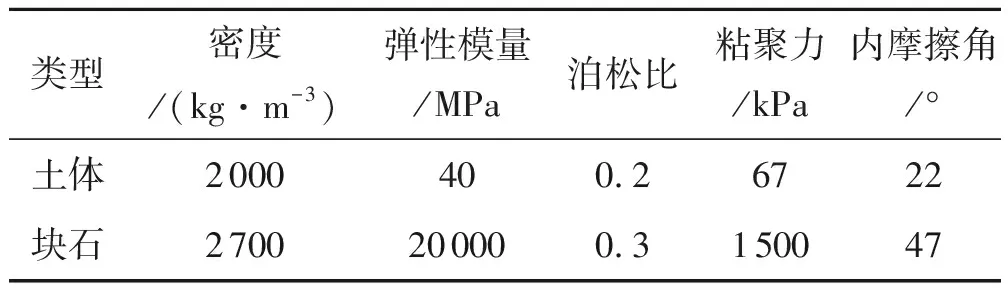
表1 土石混合介质力学参数

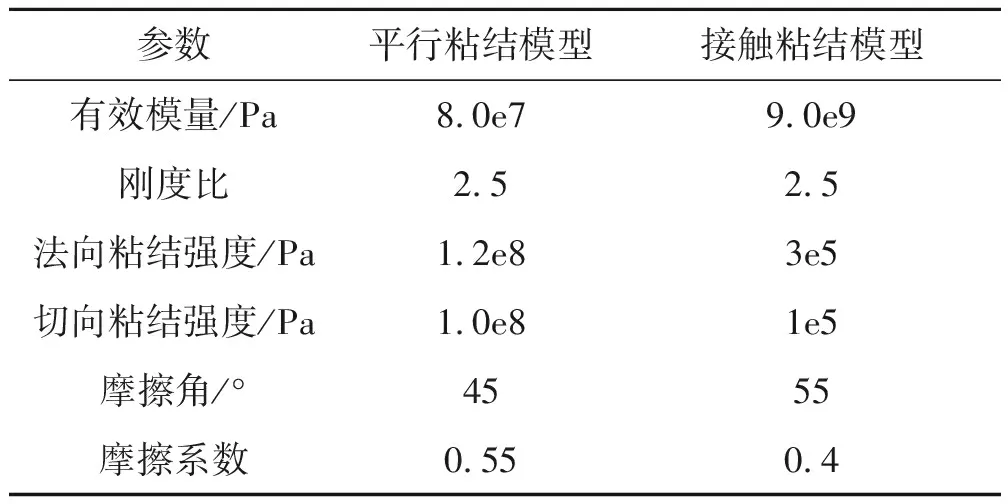
表2 离散元模型参数

4 直剪试验下土石混合介质力学特性分析

4.1 剪切应力-位移曲线

如图8所示的不同法向应力下土石混合介质的剪切应力-位移曲线，土石混合介质的剪切应力-位移曲线整体分为峰前峰后两个阶段．

图8 不同法向应力下土石混合介质剪切应力-位移关系曲线

峰前阶段，随着剪切位移的增大，剪切应力也在逐渐增大，剪切应力和剪切位移呈现出非线性的变化趋势．随着法向应力的增加，剪切应力峰值也在逐渐增加．峰后阶段，随着剪切位移的增大，剪切应力先减小，经历一定剪切位移后又继续增大，这是由于在峰值处，土石混合介质中的颗粒旋转到一定位置，颗粒间的初始咬合断裂，造成剪切应力下降，随着剪切位移的增加，土石介质间形成新的咬合，导致剪应力升高．对于同一试样，法向应力越大，这种新的咬合作用表现得越明显，因此，随着法向应力的增加，剪切应力峰值也在不断增加．另外，随着剪切位移的增大，模型中逐渐形成不规则的剪切带．相同剪切位移下，法向应力越大，对应的剪切带也越大，即块石间的相互作用随着法向应力的增大而增大．

4.2 颗粒间接触力的演化过程

在直剪过程中，为了抵抗剪应力，试样内部颗粒间接触力的大小和方向会发生一定的调整，通过分析剪切过程中试样内部力链网络和接触组构的演化过程，可以清楚地了解剪切过程中土石颗粒间接触力的相互传递演化过程．

图9为法向应力200 kPa下不同剪切位移下的力链网络分布规律，其中，图9(a)～(d)剪切位移分别为0，1，2，12 mm．可见，伺服完成后，剪切盒内整体稳定，力链在剪切盒内均匀分布，表明此时剪应力是由土体和石块两者共同来承担的，且石块与土体颗粒所承担的剪应力大小基本相同．随着剪切的开始，由于受剪切带处剪切作用，该处产生大量强力链而其他位置的力链多为弱力链．在峰值应力状态前，剪切盒中右上和左下部分的力链分布发生明显变化，而试样中部的力链仍保持竖直．在峰值应力状态处，试样中部力链的分布特征发生完全改变，强力链分布在右上、左下以及剪切带位置，其中剪切带位置的力链逐渐沿30°至45°方向倾斜．随着剪切的继续进行，强力链进一步增强，但其方向基本保持30°至45°方向．

图9 法向应力200 kPa下不同剪切位移时的力链网络分布规律

图10为法向应力200 kPa不同剪切位移下的接触力分布规律，其中图10(a)～(d)剪切位移分别为0，1，2，12 mm．可见，初始阶段的各个方向接触力的大小分布比较均匀，分布形状类似于一个圆，随着剪切位移的增加，为了抵抗剪切变形，颗粒间接触力发生明显变化，分布形状由圆形逐渐变成椭圆形，且椭圆的长轴方向与剪切面形成一定角度．在到达峰值应力时，椭圆形状变得扁平，试样内部颗粒间的接触力沿着抵抗剪切方向逐渐增大．当剪切应力到达峰值之后，随着剪切位移的增加，试样内部颗粒间的接触力沿着抵抗剪切方向也将逐渐减小，导致椭圆的长短轴之比减小，椭圆形状明显变得粗壮．随着剪切位移的增加，剪切应力大小基本不变，试样内部颗粒间的接触力也将保持不变．

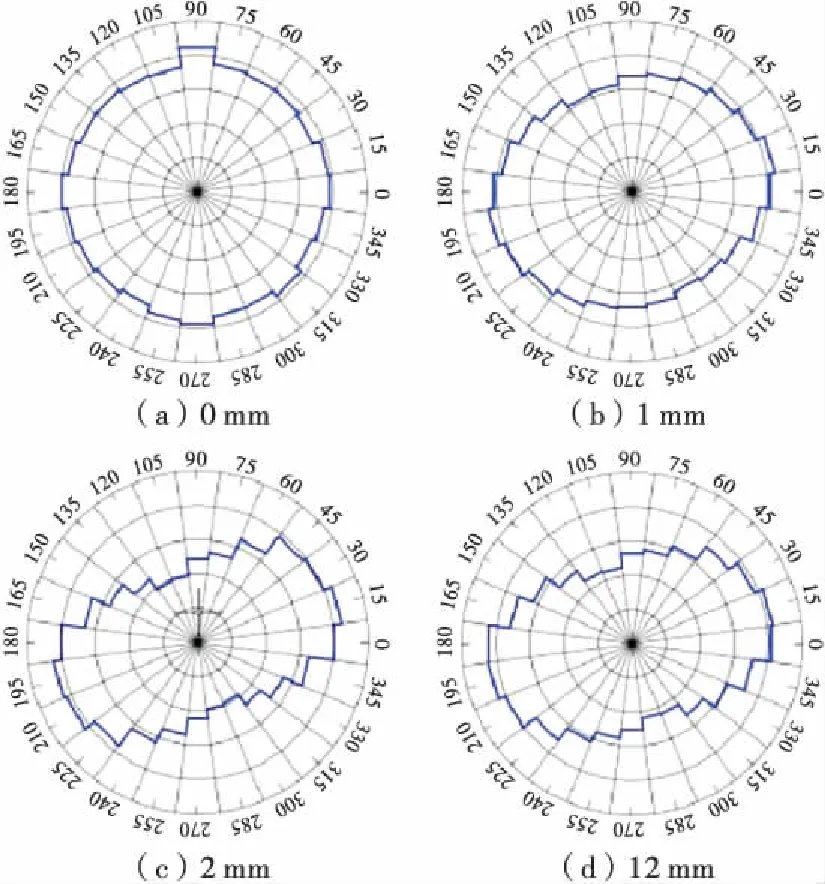
图10 法向应力200 kPa下不同剪切位移时的接触分布规律

5 结 论

采用土石混合介质数字图像，建立了土石混合介质的离散元模型，并对土石混合介质进行了二维直剪试验，得到了以下结论：

1)基于数字图像识别的土石混合介质离散元模型开展直剪试验数值模拟，可保证土石混合介质中的块石分布情况与实际情况一致．

2)应用区域生长算法可以实现土石混合介质的分割，可将具有相同特征的土和石块识别出来，并且保留清晰的边界轮廓信息和分割效果，克服了简单灰度分割方法中可能出现的欠分割和过度分割等缺陷．

3)通过颗粒间的组构分布和力链传递关系直接反映试样内部的颗粒间接触以及接触力的变化情况，可作为现场试验的补充，从微观角度反映土石混合介质在直剪试验下的力学性质．